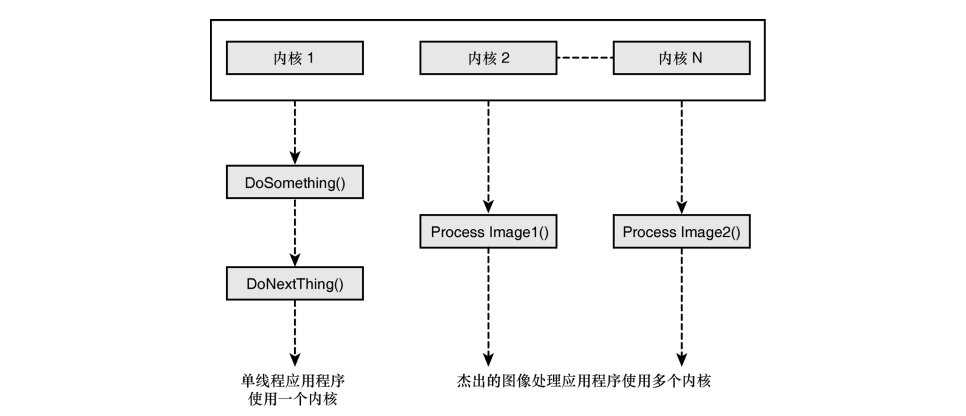
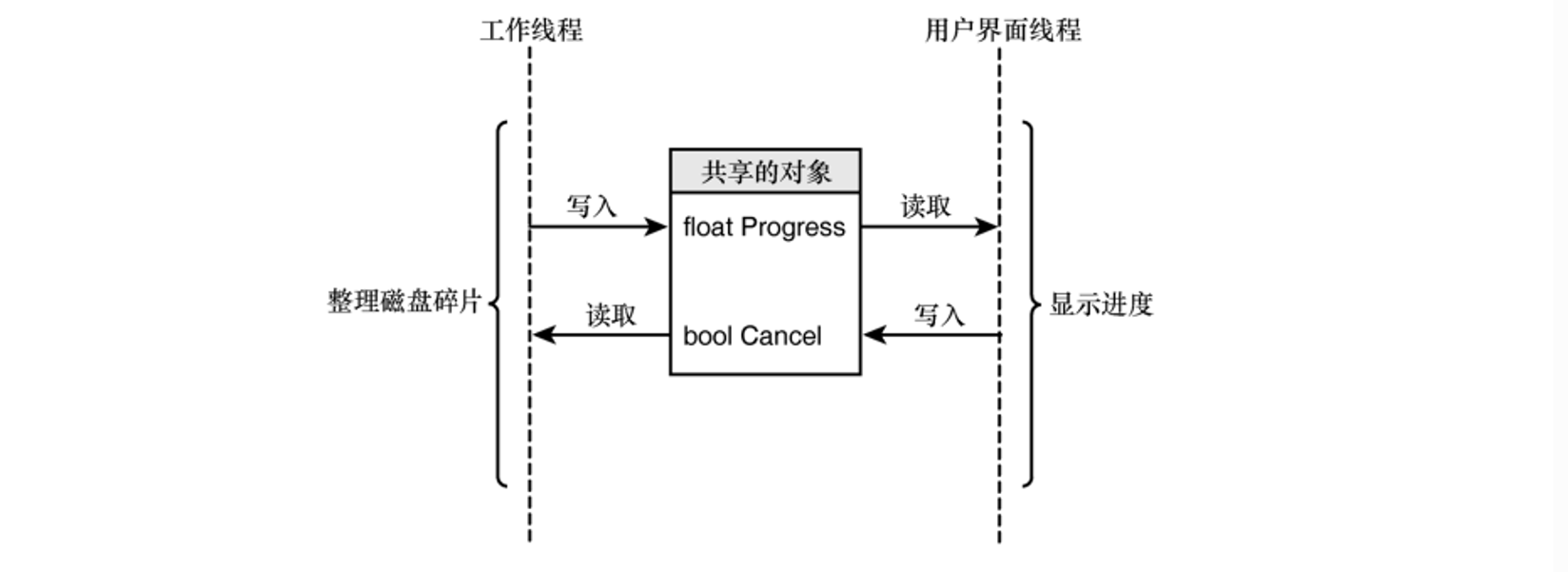
一、 AI与机器学习基础概念 什么是人工智能(AI)、机器学习(ML)和深度学习(DL)?它们之间有什么关系? AI是一个广泛的概念,指让机器模仿人类智能。ML是实现AI的一种方法,让机器从数据中学习。DL是ML的一个子集,使用深度神经网络(多层)进行学习。
机器学习主要有哪几类?请分别举例说明。 监督学习 (Supervised Learning): 使用“有标签”的数据。例如:房价预测(回归)、垃圾邮件分类(分类)。无监督学习 (Unsupervised Learning): 使用“无标签”的数据。例如:用户分群(聚类)、降维(如PCA)。强化学习 (Reinforcement Learning): 通过“奖励”和“惩罚”学习。例如:AlphaGo下棋、自动驾驶策略。什么是“过拟合”?什么是“欠拟合”? 过拟合指模型在训练集上表现很好,但在测试集上表现很差(泛化能力弱)。欠拟合指模型在训练集上表现就不好。
有哪些方法可以防止或缓解过拟合? 获取更多数据。 数据增强 (Data Augmentation)。 使用更简单的模型。 正则化 (Regularization) (L1, L2)。Dropout (在神经网络中常用)。早停 (Early Stopping)。 解释一下“偏差” (Bias) 和“方差” (Variance) 以及它们之间的权衡。 高偏差通常导致欠拟合(模型太简单),高方差通常导致过拟合(模型太复杂)。理想的模型是低偏差且低方差,但两者往往是此消彼长的。
二、 机器学习算法与模型 请解释一下线性回归的原理。 找到一条直线(或超平面)来最好地拟合数据点。关键是定义 损失函数 (Loss Function),通常使用均方误差 (MSE),然后通过优化算法(如梯度下降)最小化损失函数来求解参数。
逻辑回归和线性回归有什么区别? 逻辑回归是用来做分类 任务的(尤其是二分类),线性回归是用来做回归 (预测连续值)任务的。逻辑回归在线性回归的基础上,套用了一个Sigmoid函数,将输出值映射到0到1之间,表示概率。
什么是决策树?它的优缺点是什么? 优点是可解释性强、能处理非线性数据。缺点是容易过拟合。
什么是随机森林?它如何改进决策树? 随机森林是 集成学习 (Ensemble Learning) 中 Bagging 的一种。它通过构建多棵决策树,并让它们投票(分类)或取平均值(回归)来减少单棵决策树过拟合的风险。
简单介绍一下K近邻 (KNN) 算法。 “近朱者赤,近墨者黑”。它是一种懒惰学习(Lazy Learning),预测时才计算。对于新数据点,找到训练集中离它最近的K个点,然后根据这K个点的标签来决定新数据点的标签。
简单介绍一下K-Means聚类算法。 无监督学习。目标是将数据分成K个簇(Cluster)。步骤:1. 随机选K个中心点。2. 将每个数据点分配给最近的中心点。3. 重新计算每个簇的中心点(均值)。4. 重复2和3直到中心点不再变化。
三、 数据预处理与特征工程 为什么需要对数据进行“归一化” (Normalization) 或“标准化” (Standardization)? 解决不同特征(如“年龄”和“收入”)量纲(尺度)不同的问题。这可以加速梯度下降的收敛速度,并提高一些算法(如KNN、SVM)的准确性。
归一化 (Min-Max Scaling): 将数据缩放到 [0, 1] 区间。标准化 (Z-score Standardization): 将数据转换成均值为0,标准差为1的正态分布。何处理缺失值? 删除(删除行或列)。 填充(使用均值、中位数、众数填充)。 使用模型预测填充。 如何处理类别型特征? 标签编码 (Label Encoding): 将 “红”, “绿”, “蓝” 编码为 0, 1, 2。适用于有序类别。独热编码 (One-Hot Encoding): 将 “红”, “绿”, “蓝” 编码为 [1,0,0], [0,1,0], [0,0,1]。适用于无序类别。四、 模型评估 在分类任务中,有哪些常用的评估指标? 准确率 (Accuracy): 预测正确的样本数 / 总样本数。精确率 (Precision): $TP / (TP + FP)$。在所有预测为“正”的样本中,有多少是真的“正”。召回率 (Recall): $TP / (TP + FN)$。在所有真的“正”样本中,有多少被成功预测出来了。F1-Score: 精确率和召回率的调和平均数, $2 \cdot (Precision \cdot Recall) / (Precision + Recall)$。什么时候更关注精确率,什么时候更关注召回率? 关注精确率(宁可少抓,不可错抓): 垃圾邮件检测。你不想把重要邮件误判为垃圾邮件 (FP要低)。关注召回率(宁可错抓,不可漏抓): 癌症诊断。你不想把癌症患者漏诊 (FN要低)。什么是混淆矩阵? 一个表格,用于可视化分类模型的性能。包含四个值:真正 (TP), 假正 (FP), 真负 (TN), 假负 (FN)。
什么是交叉验证?为什么需要它? 为了更可靠地评估模型的泛化能力,防止数据划分的偶然性。最常用的是K折交叉验证(K-Fold Cross-Validation),将数据分成K份,轮流用其中K-1份训练,1份测试,最后取K次评估结果的平均值。
五、 深度学习基础(初级) 什么是神经网络 (Neural Network)?它由哪些基本部分组成? 输入层、隐藏层、输出层。神经元(节点)、权重 (Weights)、偏置 (Biases)、激活函数 (Activation Function)。
为什么需要激活函数?常用的激活函数有哪些? 为了给模型引入非线性 。如果不用激活函数,多层神经网络也只相当于一个线性回归。
Sigmoid: $1 / (1 + e^{-x})$,输出在 (0, 1) 之间。ReLU (Rectified Linear Unit): $\max(0, x)$。目前最常用,计算快,能缓解梯度消失。Tanh: 输出在 (-1, 1) 之间。什么是梯度下降 (Gradient Descent)? 一种优化算法,用来最小化损失函数。通过计算损失函数对参数的梯度 (导数),然后沿着梯度的反方向 小步更新参数。
解释一下 Epoch, Batch, Iteration 的区别。 Epoch (时代): 所有训练数据完整地训练一遍。Batch (批次): 将训练数据分成N个批次。Iteration (迭代): 训练一个Batch所需的步骤。 1个Epoch = N个Iteration (N = 总样本数 / Batch Size)。简单介绍一下CNN(卷积神经网络)主要用在什么地方? 主要用于图像处理 。它的核心是卷积核 (Kernel) ,通过卷积操作提取图像的局部特征(如边缘、纹理)。
简单介绍一下RNN(循环神经网络)主要用在什么地方? 主要用于序列数据 (如文本、时间序列)。它的特点是神经元的输出可以作为下一次的输入,使其具有“记忆”功能,能处理上下文依赖关系。
六、 LLM细分领域 什么是词嵌入 (Word Embedding)? 将词语(离散符号)映射到低维连续向量空间的过程。关键思想是让语义相近的词在向量空间中的距离也相近。
你知道哪些词嵌入技术?它们有什么区别? Word2Vec (CBOW/Skip-gram): 静态词向量。通过上下文预测中心词 (CBOW) 或通过中心词预测上下文 (Skip-gram)。GloVe: 静态词向量。利用全局共现矩阵。BERT/ELMo: 动态/上下文相关的词向量。同一个词在不同句子中的向量是不同的。什么是 “Bank” 问题(一词多义)?Word2Vec 如何处理?BERT 如何处理? Word2Vec 无法处理。”bank”(银行)和 “bank”(河岸)的词向量是相同的。BERT 可以处理,因为它会根据上下文(”I went to the bank to deposit money” vs “I sat on the river bank”)生成不同的向量。
什么是 Tokenization (分词)?LLM 中常用哪种方式? BPE (Byte Pair Encoding) 或 SentencePiece。
为什么不用词作为单位? 词表会过大(数百万),且无法处理未登录词 (OOV, Out-of-Vocabulary)。为什么不用字符作为单位? 序列会过长,单个字符的语义信息太少。BPE 的优势: 介于词和字符之间,通过合并高频字节对来构建词表,既能控制词表大小,又能很好地处理生僻词和拼写错误。这是LLM的基石,必考领域 。
解决 RNN/LSTM 的两个主要问题:
无法并行计算 (必须按顺序处理);长距离依赖捕获困难 (信息在长序列中传递会丢失)。请解释一下自注意力机制的工作原理。 这是核心中的核心。简单说,就是让模型在处理一个词时,能“关注”到句子中所有其他词,并计算一个“注意力权重”分布,来决定哪些词对当前词的理解更重要。
什么是 $Q$ (Query), $K$ (Key), $V$ (Value)?它们是如何计算的? $Q, K, V$ 都是从同一个输入向量(词嵌入)通过不同的线性变换(乘以权重矩阵 $W_q, W_k, W_v$)得到的。
计算过程:
用 $Q$ 和 $K$ 计算相似度(通常是点积:$Q \cdot K^T$)。 用 $\text{Softmax}$ 将相似度得分归一化为注意力权重。 用这个权重对 $V$ 进行加权求和,得到最终的输出。 公式(不一定要背,但要理解):$\text{Attention}(Q, K, V) = \text{softmax}(\frac{QK^T}{\sqrt{d_k}})V$ 为什么要除以 $\sqrt{d_k}$? 放 (Scaling)。防止点积结果过大,导致 $\text{Softmax}$ 函数进入梯度很小的区域,使得梯度消失,训练不稳定。
什么是多头注意力 (Multi-Head Attention)?为什么需要它? 将 $Q, K, V$ 拆分成 $h$ 个“头”(Head),分别进行注意力计算,最后再把 $h$ 个头的结果拼接起来。允许模型在不同的“表示子空间”中学习信息。好比“从不同角度去审视”这个句子。
因为 Self-Attention 机制本身是位置无关 的(它只看词与词之间的关系,不看谁在谁前面)。
必须有一个东西告诉模型词的顺序信息。位置编码就是给每个位置的词嵌入加上一个独特的位置向量(通常用 $\sin$ 和 $\cos$ 函数生成)。
残差连接: $x + \text{SubLayer}(x)$。解决深度神经网络中的梯度消失 问题,让梯度可以“抄近道”传递,使训练非常深的网络成为可能。层归一化: 在特征维度 上进行归一化。帮助稳定训练过程,加速收敛。三、 LLM 架构与代表模型 LLM 主要有哪些架构?它们分别适用于什么任务? Encoder-Only (编码器架构): 如 BERT, RoBERTa。双向上下文。适用于自然语言理解 (NLU) 任务,如分类、命名实体识别 (NER)、问答。Decoder-Only (解码器架构): 如 GPT 系列 (GPT-3, ChatGPT), LLaMA。单向上下文(Causal LM)。适用于自然语言生成 (NLG) 任务,如文本续写、对话。Encoder-Decoder (编码器-解码器架构): 如 T5, BART。适用于序列到序列 (Seq2Seq) 任务,如翻译、摘要。BERT 的预训练任务是什么? MLM (Masked Language Model, 掩码语言模型): 随机遮盖 (Mask) 掉句子中 15% 的词,让模型去预测这些被遮盖的词是什么。这迫使模型学习双向上下文。NSP (Next Sentence Prediction, 下一句预测): 判断两个句子是否是原文中连续的。GPT 的预训练任务是什么? Causal Language Model (CLM, 因果语言模型),也就是“下一个词预测”。模型只能看到当前词以及它之前的所有词,来预测下一个词。
什么是 “In-Context Learning” (上下文学习)? 什么是 Zero-shot, One-shot, Few-shot? 是 GPT-3 带来的一个重要能力。不需要更新模型参数(不需要微调),只在提示词 (Prompt) 中给模型几个例子,模型就能“学会”如何做这个新任务。
Zero-shot: 不给例子,直接给指令。One-shot: 给 1 个例子。Few-shot: 给 2 个或更多例子。四、 训练、微调与对齐 什么是预训练 (Pre-training) 和微调 (Fine-tuning)? 预训练: 在海量的、无标签的文本数据上,使用自监督任务(如 MLM 或 CLM)训练一个通用的基础模型。这个过程非常昂贵。微调: 在预训练好的模型基础上,使用一个小的、有标签的、针对特定任务的数据集,继续训练模型,使其“适配”这个任务。么是 RLHF?它主要分为哪几个步骤? RLHF (Reinforcement Learning from Human Feedback, 基于人类反馈的强化学习): 这是让 ChatGPT 如此“听话”和“有用”的关键技术,用于模型对齐 (Alignment) 。
步骤:
SFT (Supervised Fine-Tuning): 收集高质量的“指令-回答”数据,对预训练模型进行有监督微调。训练奖励模型 (Reward Model, RM): 用 SFT 模型对同一个指令生成多个回答 (A, B, C, D),然后请人类标注员对这些回答进行排序。用这个排序数据训练一个 RM,使其能给“好的”回答打高分,给“坏的”回答打低分。RL 强化学习 (PPO 算法): 用 SFT 模型作为策略 (Policy),用 RM 作为奖励函数,使用强化学习(如 PPO)来优化模型,使其生成的回答能获得 RM 的高分。什么是 PEFT?你了解哪些 PEFT 技术? PEFT (Parameter-Efficient Fine-Tuning, 参数高效微调): 在微调 LLM 时,只训练模型的一小部分参数,而不是全部参数(如 175B 个)。
全参数微调成本太高(需要几十到几百 GB 的显存)。
例如 LoRA (Low-Rank Adaptation) 核心。冻结原始权重 $W$,在旁边加一个低秩矩阵 $W + \Delta W = W + BA$。只训练 $B$ 和 $A$(参数量远小于 $W$)。
五、 应用、挑战与前沿 什么是 RAG (Retrieval-Augmented Generation)? 这是目前最主流的 LLM 应用范式,非常重要 。
工作原理: 当用户提问时,系统首先 去一个外部知识库(如向量数据库)中检索 (Retrieval) 相关的文档片段,然后把这些文档片段和用户的原始问题一起拼接 (Augmented) 成一个新的 Prompt,最后交给 LLM 去生成 (Generation) 答案。RAG 解决了 LLM 的什么问题? 缓解模型幻觉 (Hallucination): 答案被“锚定”在检索到的事实上,而不是模型自己“编造”。知识更新: LLM 的知识是静态的(训练截止日期)。RAG 可以通过更新外部知识库,让 LLM 回答最新的问题。可解释性/溯源: 可以告诉用户答案是基于哪些文档生成的。什么是向量数据库 (Vector Database)? 门用于存储和高效查询向量 (Embedding) 的数据库。RAG 的核心组件之一。
LLM 目前面临哪些主要挑战? 幻觉 (Hallucination): 编造事实。上下文窗口 (Context Window) 限制: 能处理的文本长度有限(虽然现在越来越长)。成本高昂: 训练和推理都需要强大的算力。数据偏见 (Bias) 与安全性。 Python与工具库 你常用哪些Python库来做AI开发? NumPy: 科学计算,处理多维数组 (N-dimensional Array)。Pandas: 数据分析和处理,核心是 DataFrame 和 Series。Scikit-learn (sklearn): 传统的机器学习库,包含大量算法、预处理和评估工具。TensorFlow / PyTorch: 深度学习框架。Pandas中 loc 和 iloc 有什么区别? loc 是基于标签 (label) 的索引。iloc 是基于位置 (integer position) 的索引。你如何用 Scikit-learn 训练一个完整的机器学习模型? 加载数据 (load_data)。 数据预处理 (preprocessing)。 划分训练集和测试集 (train_test_split)。 初始化模型 (e.g., model = LogisticRegression())。 训练模型 (model.fit(X_train, y_train))。 评估模型 (model.score(X_test, y_test))。 核心框架(模型开发与训练) 这是构建和训练 LLM 本身的基础。
PyTorch: 用途: 目前 LLM 领域事实上的标准 。绝大多数前沿研究(包括 GPT、LLaMA 等模型的原始实现)和开源项目都基于 PyTorch。它提供了灵活的张量计算和动态计算图,非常适合复杂的模型架构。面试重点: 必须熟悉。TensorFlow / Keras: 用途: 另一个主要的深度学习框架。虽然在 LLM 研究领域的热度稍逊于 PyTorch,但在 Google 内部(如 PaLM, Gemini)和许多企业的生产环境中仍有广泛应用。Keras 提供了更高级、更易用的 API。2. Hugging Face 生态(事实上的工具标准) Hugging Face (HF) 提供了一套“全家桶”,极大地简化了 LLM 的使用和开发。
transformers:用途: 核心中的核心 。它提供了一个统一的 API,让你可以在几行代码内加载、训练和使用几乎所有主流的 Transformer 模型(如 BERT, GPT-2, LLaMA, T5 等)。它内置了模型架构、预训练权重、分词器 (Tokenizer) 和配置。面试重点: 初级岗位必须熟练使用。datasets:用途: 高效处理和加载海量文本数据集(GB 甚至 TB 级别)。它支持流式 (streaming) 加载、内存映射 (memory mapping) 和强大的数据预处理(如 map 操作),是预训练和微调必备的工具。tokenizers:用途: transformers 库背后的高性能分词器库。它提供了 BPE, WordPiece 等主流分词算法的快速实现。accelerate:用途: 简化 PyTorch 的分布式训练和混合精度训练 。只需添加几行代码,就能让你的训练脚本轻松地在多 GPU、TPU 或多台机器上运行。evaluate:用途: 方便地加载和计算各种 NLP 评估指标,如 BLEU, ROUGE (用于摘要/翻译) 或 PPL (Perplexity, 困惑度,用于评估语言模型本身)。3. LLM 应用框架(构建应用) 当你不训练 模型,而是调用 模型(如 GPT-4 API 或开源模型)来构建 RAG、Agents 等应用时,会用到这些框架。
LangChain: 用途: 目前最火的 LLM 应用开发框架。它是一个“胶水”层,帮你编排(Orchestrate) LLM 调用的各个环节。核心功能: Prompt 模板管理、Chains(将多个 LLM 调用或工具调用链接起来)、Agents(让 LLM 决定使用哪些工具)、Memory(给对话添加记忆)、RAG(文档加载、切分、检索)。LlamaIndex: 用途: 另一个流行的框架,它更专注于 RAG (检索增强生成)。在数据摄入、索引构建和检索查询方面通常被认为更强大和灵活。Semantic Kernel: 用途: 微软开源的框架,思路与 LangChain 类似,但在 C# 和 Python 中都有实现,更侧重于与微软生态(如 Azure)的集成。4. 向量数据库(RAG 的 “记忆”) RAG 是 LLM 最核心的应用之一,而向量数据库是 RAG 的基础。
ChromaDB (Chroma): 用途: 开源、轻量级、内存优先的向量数据库。非常适合快速原型设计和中小型项目,与 LangChain/LlamaIndex 集成度很高。FAISS: 用途: Facebook AI (Meta) 开源的向量库 (不是数据库)。它提供了极其高效的向量相似度搜索算法,但本身不带数据库管理功能。通常被用作其他数据库的底层索引引擎。Pinecone / Weaviate / Milvus: 用途: 生产级别的、可扩展的向量数据库。当你需要处理数十亿级别的向量、需要高可用和复杂的元数据过滤时,会选择它们。5. 推理与服务(部署) 当你需要将训练好的模型部署为 API 时使用。
FastAPI: 用途: 目前 Python 领域最快、最流行 的 Web 框架之一,特别适合构建 ML/AI 模型的 API 服务。它基于 ASGI(异步),性能极高,并且自带 Swagger UI 自动生成 API 文档。Flask: 用途: 轻量级的传统 Web 框架。对于简单的模型 API 仍然是一个不错的选择,但性能不如 FastAPI。vLLM / TGI (Text Generation Inference): 用途: 专门为 LLM 设计的高性能推理服务器。它们通过 PagedAttention、连续批处理 (Continuous Batching) 等技术,极大提升 LLM 的推理吞吐量(每秒处理的请求数)。bitsandbytes / auto-gptq:用途: 模型量化 (Quantization) 库。用于将模型从 FP16/FP32 压缩到 8-bit 甚至 4-bit,从而在消费级显卡(如 3090, 4090)上运行大型模型。LLM简要推理流程 LLM 的推理是一个自回归 (Autoregressive) 的过程,它分两个主要阶段:预填充(Pre-fill)/提示处理阶段 和 解码(Decoding)/生成阶段 。简单介绍下 LLM 推理流程 (以 Transformer Decoder-Only 架构为例)
阶段一:输入处理 这一阶段的目标是将用户的整个输入文本 (Prompt) 转化为模型可以处理的内部状态。
步骤 动作 1. 输入文本 用户输入一段文本。 2. 分词 (Tokenization) 文本 -> Token (词元) 。分词器将连续的文本分割成模型能理解的基本单元(Tokens)。一个 Token 可能是一个单词、一个子词、一个标点符号,或者是一个特殊标记。分词器输出是整数 ID 序列。3. 词嵌入 (Embedding) Token ID -> 向量 。模型通过查表操作,将每个 Token ID 转换为一个固定维度的词嵌入向量 。嵌入层将离散的 ID 转换为连续的浮点数向量,这些向量包含了词的语义信息。4. 位置编码 (Positional Encoding) 在嵌入向量中加入位置信息 ,因为 Transformer 结构本身不包含序列顺序的概念。通常是固定的三角函数编码或可学习的相对/绝对位置编码 (如 RoPE)。
阶段二:计算与预测 解码阶段 这一阶段模型开始根据输入状态和前面生成的 Tokens,一次生成一个新 Token 。
步骤 动作 5. 自注意力计算 (Self-Attention) 模型计算当前序列中所有 Token 之间 的相互关系和重要性(即注意力分数 )。每一个token通过 Q (Query), K (Key), V (Value) 三个向量计出三组向量。 6. 计算注意力分数 将 Query 向量 与 Key 向量进行点积,衡量它们之间的相似度。对点积结果进行缩放 (稳定梯度)。应用 Softmax 函数 ,将相似度分数转换为权重(注意力分数),确保权重总和为 1。 7. 上下文向量生成 模型使用注意力分数对 Value 向量(V)进行加权求和 ,得到一个上下文向量 ,这个向量包含了序列中所有相关信息。加权求和结果(上下文向量)进入后续的前馈网络。 8. 前馈网络 (FFN) 与残差连接 上下文向量经过多层 Transformer Blocks 中的前馈网络 和残差连接 ,进一步提炼特征。这是Transformer 的核心组成部分,增加模型的非线性表示能力。 9. 预测 (Logits) 与采样 最终的向量经过顶部的线性层和 Softmax 函数,输出一个概率分布Logits,维度等于模型的词汇表大小。Logits 告诉模型下一个 Token 可能是词汇表中的哪个词。根据采样策略的概率分布选择下一个 Token。在线性层,Softmax + 采样器 通常会加入温度参数以控制随机性。 10. 缓存 Key 和 Value (KV Cache) 在生成阶段,每生成一个 Token,其计算出的 K 和 V 向量会被缓存。在下一轮迭代时,可以直接使用这些缓存,而无需重新计算前面所有 Token 的 K 和 V,大大提高速度。这是LLM 加速的关键。 11. 自回归循环 新 Token -> Token ID -> 嵌入 ,将其作为下一轮输入序列的最后一个 Token,重复步骤 5-9。直到循环达到停止条件。
阶段三:预测完结标志 (Termination) LLM 的生成过程不是无限的,它会在满足以下停止条件 之一时终止:
生成特殊结束标记 (End-of-Sequence, EOS) :模型在预测的 Logits 中给出一个特殊的 <EOS> 或 <end> Token 最高的概率,这是最主要的 自然完结标志 。达到最大长度限制 (Max Tokens) :预设的生成 Token 数量限制已达到(例如,限制最多生成 128 个 Token)。生成了停止词 (Stop Words) :模型输出了用户预设的停止词,例如用户在问答应用中设置了句号或换行符为停止词。张量的使用 前面的文章介绍了自注意力机制,这个是现代LLM的核心机制,它允许模型在处理序列数据(如文本)时,能够关注不同位置的信息。而这整个过程中,原始数据,KQV权重,偏差等等,都是通过 张量(Tensor) 的存储和高效计算来实现的。
权重 (Weights) 在神经网络中,权重是模型学习到的、用来决定输入数据重要性的参数。权重 的作用是决定一个神经元从上一层接收到的众多信号中,哪些是重要 的,哪些是不重要 的。
它们本质上是乘数,应用于输入数据 (x)。一个输入值乘以一个权重 (w) 后,就会进入下一层的神经元。
权重的大小决定了该输入特征对下一层神经元的影响程度。权重越大,表示对应的输入特征越重要,对最终输出的影响也越大。权重越小(接近零),表示该特征不太重要。
在 模型训练过程中 ,算法(如梯度下降)会不断调整这些权重的值,直到模型能够准确地完成任务(例如,正确识别图片中的物体)。
权重 是模型在训练过程中学到的,用来对输入特征进行 优先排序 和 量化重要性 的参数。它是模型的核心“知识”。
举一个例子,想象你正在做饭(输出),你需要考虑以下输入:
输入 含义 x_1食材的新鲜度 x_2厨师的经验 x_3餐具的精致度
在模型训练之前,这三项对“味道好不好”的贡献是未知的。模型通过学习,会给它们分配 权重 (w):
如果模型发现“食材的新鲜度”对味道影响最大 ,它会给 x_1 分配一个很高的 权重 w_1 (比如 w_1 = 5.0)。如果模型发现“餐具的精致度”对味道影响很小 ,它会给 x_3 分配一个很小的 权重 w_3 (比如 w_3 = 0.1)。权重在公式中的体现 每个输入值都会被它对应的权重放大或缩小 ,然后所有结果相加: \[\text{加权输入} = w_1 x_1 + w_2 x_2 + w_3 x_3 + \dots\]
偏差 (Biases) 偏差是模型学习到的另一个参数,通常添加到权重乘以输入值的乘积之和上。
它是一个 加数(b) ,用于平移或调整神经元的激活输出。在计算中,它通常位于激活函数之前。偏差 的作用是提供一个额外的、独立于输入 的恒定值,用于调整神经元的激活阈值,让它更容易或更难被“激活”。
偏差 允许神经元在所有输入都是零的情况下仍能产生一个非零的激活输出。它赋予了模型更大的灵活性,使其能够更好地拟合数据。如果没有偏差,决策边界(Decision Boundary)将必须穿过原点,这会极大地限制模型的表达能力。
即 偏差 允许模型在不改变任何权重的情况下,平移 (Shift)激活函数曲线。这使得模型能更好地捕捉和拟合数据中的各种模式,是调整 决策边界 的关键。
像权重一样,偏差的值也是在训练过程中不断学习和调整的。
1. 偏差独立于输入 (+ b) 沿用做饭的例子: \[\text{加权输入} = (w_1 x_1 + w_2 x_2 + w_3 x_3)\]
如果所有的输入 x 都很差(都是 0),那么加权输入就是 0。这意味着无论你使用什么激活函数,输出可能总是很低。
偏差 (b) 的引入打破了这个限制:
如果模型学到一个正的偏差 (b = +2.0),它就像是一个“基准分”。即使所有食材 (x) 都很普通,最终的味道(输出)也会有一个较高的起始点。这使得神经元更容易被激活。 如果模型学到一个 负的偏差 (b = -2.0),它就像是一个“惩罚分”。这使得神经元必须接收到非常好的加权输入,才能被激活。 偏差公式中的体现 偏差 (b) 在加权输入求和之后被简单地 加上 去: \[\text{神经元的净输入} (z) = \underbrace{(w_1x_1 + w_2x_2 + \dots)}_{\text{加权输入}} + \underbrace{b}_{\text{偏差}}\]
这个 净输入z 随后会送入激活函数 ,以产生该神经元的最终输出。
前向推理流程 以 自注意力机制(Self-Attention) 为例,详细说明张量如何组织数据、存储参数和执行计算。
这个过程是 Transformer 模型核心组件 “缩放点积注意力” (Scaled Dot-Product Attention) 的关键步骤。它的目的是让模型在处理一个词(Token)时,能够 动态地衡量输入序列中所有其他词与这个词的相关性 ,然后根据这个相关性(即注意力权重)来构造这个词的新的、包含上下文信息的表示。
整个计算过程可以分解为以下几个步骤:
1. 输入:词嵌入 (Token Embeddings) 当用户输入一句话时,模型会先将自然语言划分token,然后输入句子中的每个词或子词的Token都会被转换成一个固定维度的向量,称为词嵌入。
转换后的总输入的张量名称为 X ,张量形状为 (序列长度, 嵌入维度)
如果输入是 4 个词,每个词用 1024 维的向量表示,则 X 的形状是 (4, 1024) 。它们的嵌入向量分别是 x_1, x_2, …, x_4 。
2. 生成 Q, K, V 向量 对于序列中的每一个 词嵌入 x_i,我们都通过乘以三个不同的、可学习的权重矩阵 (W_Q, W_K, W_V) 来生成它对应的 Query (查询)、Key (键)、和 Value (值) 三个向量。
Query (Q_i) : 代表当前 Token 为了理解自己而去主动发出的“查询”。Key (K_i) : 代表当前 Token 的“可被查询”的特征或“标签”。Value (V_i) : 代表当前 Token 实际包含的信息。数学上表示为: \[Q_i = x_i \cdot W_Q \\ K_i = x_i \cdot W_K \\ V_i = x_i \cdot W_V\]
这个操作会对序列中的所有 Token 进行,最终我们会得到三组向量矩阵 Q, K, V。如果输出维度也是 1024,则这三个权重张量都是 (1024, 1024) 的 2 维矩阵。它们是模型的永久知识 。
传统的编程需要一个 for 循环,遍历 4 个词,分别计算。但使用张量,这 4 个词的计算是一次性并行完成 的,这正是深度学习速度飞快的原因。
3. 计算注意力分数 (Attention Scores) 现在,为了计算某个特定 Token(比如第 i 个 Token)应该对序列中其他所有 Token(包括它自己)投入多少“注意力”,我们需要用它的 Query 向量 (Q_i) 与所有 Token 的 Key 向量 (K_j) 进行点积运算。
Score(i, j) = \[Q_i \cdot K_j\]
这个点积的结果是一个标量(一个数字),它衡量了 Token i 和 Token j 之间的“相关性”或“匹配度”。如果 Q_i 和 K_j 的方向越接近,点积的结果就越大,意味着它们越相关。
点积在数学上的定义为: \[A \cdot B = |A| |B| \cos(\theta)\]
这里每个词向量取模都一样可以互相抵消,所以 结果的大小就代表了两个向量在空间内部的距离远近 。最后的结果越接近1,关联就越大。
这个 4 X 4 的张量矩阵就是注意力矩阵 ,其中的每个数值 S_ij 代表了 第 i 个词在理解语境时,应该给第 j 个词分配多少注意力 。
4. 缩放 (Scaling) 将上一步得到的原始分数除以一个缩放因子。这个因子通常是 Key(或 Query)向量维度 d_k 的平方根: \[\sqrt{d_k}\]
缩放后的分数 Scaled Score(i, j) = \[\frac{Q_i \cdot K_j}{\sqrt{d_k}}\]
为什么要缩放? 当向量的维度 d_k 很大时,点积的结果也可能会变得非常大。这会将 softmax 函数(下一步会用到)推向 梯度非常小的区域 ,导致模型在训练时梯度消失,难以学习。通过缩放,可以有效地缓解这个问题,使训练过程更加稳定。
5. Softmax 归一化 接下来,对所有缩放后的分数应用 softmax 函数。softmax 会将一组任意的实数转换成一个总和为 1 的概率分布。
Attention Weights (alpha_{ij}) = \[softmax(\frac{Q_i \cdot K_j}{\sqrt{d_k}})\]
经过这一步,我们就得到了注意力权重 或注意力分数 。alpha_{ij} 的值在 0 到 1 之间,表示 Token i 在编码自己时,应该将多少注意力放在 Token j 上。所有 alpha_{i1}, alpha_{i2}, …, alpha_{in} 的总和为 1。
6. 加权求和得到最终输出 最后,用上一步得到的注意力权重 alpha_{ij} 来对所有 Token 的 Value 向量 (V_j) 进行加权求和,得到 Token i 的最终输出向量 z_i。 \[z_i = \sum_{j=1}^{n} \alpha_{ij} \cdot V_j\]
这个输出向量 z_i 就是 Token i 的新的、融合了全局上下文信息的表示。它不再仅仅是 x_i 本身,而是整个序列中所有 Token 的 Value 的一个加权混合,权重由 Q-K 相关性决定。
加权求和,将这些注意力权重分别乘以每个词的 Value 向量,然后把它们全部加起来。例如输入为: “今天天气很”
output_vector_for_很 = 0.1 * V("今天") + 0.8 * V("天气") + 0.1 * V("很")
这个计算出的 output_vector_for_很 是一个全新的向量。它不仅包含了 “很” 本身的意思,还重点融入了 “天气” 的信息,以及少量 “今天” 的信息。这样,模型就深刻理解了 “很” 在当前上下文中的确切含义。
这个过程会 对输入序列中的每一个词都做一遍 ,最终得到一组包含了丰富上下文信息的新向量。
总结公式 如果将整个序列的 Q, K, V 看作矩阵,上述过程可以用一个简洁的公式来概括: \[\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V\]
KV 缓存 理解了上面的计算过程后,我们再来看 KV 缓存。KV 缓存是一种在模型进行自回归生成(autoregressive generation)任务(比如文本续写、对话)时,用来加速推理的关键优化技术。
场景:无 KV 缓存的低效生成 LLM 生成文本时,是一个 Token 一个 Token 地吐出来的。
生成第 1 个 Token : 模型处理输入提示(Prompt)。生成第 2 个 Token : 模型将 [原始 Prompt + 第 1 个生成的 Token] 作为新的输入,重新计算所有 Token 的 K 和 V,然后为新的位置计算 Q,再进行注意力计算。生成第 N 个 Token : 模型将 [原始 Prompt + 前 N-1 个生成的 Token] 作为新的输入,再次重新计算这 N-1 个 Token 的 Key 和 Value 向量 ,然后为第 N 个位置计算 Q,并与前面所有的 K 进行匹配。问题在哪里? 在生成第 N 个 Token 时,对于前面已经存在的 N-1 个 Token,它们的 Key 和 Value 向量是固定不变的 (因为它们的输入 Token 和模型的权重矩阵 W_K, W_V 都没有变)。每次生成新 Token 时都去重复计算这些已经算过的 K 和 V 值,是巨大的计算浪费。随着生成序列的增长,这种浪费会呈平方级增加,导致推理速度急剧下降。
解决方案:KV 缓存 KV 缓存的核心思想非常简单:计算过的东西就存起来,别再算了!
具体做法是:
在处理完初始 Prompt 后,计算出 Prompt 中所有 Token 的 Key 和 Value 向量,并将它们存储在一个缓存(Cache)中。这个缓存可以看作是模型的“短期记忆”。 当需要生成第 1 个新 Token 时,模型只需要为这个新位置计算它自己的 Q, K, V。然后,它的 Q 会与缓存中所有 已存在的 K 进行注意力计算。 计算完成后,将这个新生成的 Token 的 K 和 V 追加 到缓存中。 当需要生成第 2 个新 Token 时,重复上述过程:只为这个新位置计算 Q, K, V,然后它的 Q 与不断增长的缓存中 的所有 K 进行注意力计算,最后再把自己的 K, V 追加进缓存。 KV 缓存的优势 大幅提升推理速度 : 避免了大量的冗余计算。每次生成新 Token,计算复杂度不再与整个序列长度相关,而只与新生成的一个 Token 相关(当然,注意力计算仍然需要遍历缓存中的所有 Key)。这使得长文本的生成速度得到了质的飞跃。减少计算资源消耗 : 因为计算量减少,对 GPU/TPU 等计算单元的需求也相应降低。是流式(Streaming)输出的基础 : 我们看到的聊天机器人能够一个词一个词地快速蹦出来,背后就是 KV 缓存技术在支撑。它让模型可以高效地“接续”之前的计算,而不是每次都“从头再来”。存储的数量级 经常提到的 FP32 (Floating Point 32-bit) 和 INT4 (Integer 4-bit) 都是表示模型权重和激活值的精度单位,它们定义了存储一个数值所需的位数,直接影响了模型的大小、运行速度和精度。
FP32 (Floating Point 32-bit) 全精度 简介:
特性 描述 全称 (Full Name) 单精度浮点数 (Single-Precision Floating-Point Number) 位数 (Bits) 32 位 (4 字节) 数据结构 (Structure) 遵循 IEEE 754 标准,由以下部分组成: 符号位 (Sign) :1 位 (表示正负) 指数位 (Exponent) :8 位 (表示数量级) 尾数位 (Mantissa/Significand) :23 位 (表示有效数字精度)特点 (Characteristics) 高精度 ,表示范围广 。这是训练模型时最常用的标准精度。用途 (Use Case) 深度学习模型训练、推理阶段的基准精度、对精度要求极高的场景。 大小对比 (Size Comparison) 存储 N 个权重需要 4N 字节。
FP32 遵循 IEEE 754 标准,共 32 位,分为三个部分: \[\text{FP32} = \text{符号位 (1 位)} + \text{指数位 (8 位)} + \text{尾数位 (23 位)}\]
一个 32 位浮点数的值 V 可以表示为: \[V = (-1)^{\text{符号}} \times (1 + \text{尾数}) \times 2^{(\text{指数} - 127)}\]
其中:
符号位 (S): 第 31 位。0 为正,1 为负。指数位 (E): 第 30 到 23 位 (共 8 位)。它存储一个带偏差 (biased) 的指数。偏差值 (Bias) 为 实际指数 = 存储的指数 - 127 ,允许浮点数按其二进制表示进行 高效的数值比较和排序 。尾数位 (M): 第 22 到 0 位 (共 23 位)。尾数前面隐含一个 1 (即 1.M),所以精度是 24 位。例子:表示数字 1.0 符号位 (S): 正数 -> 0指数 (E): 1.0 = 1.0 X 2^0。所需指数为 0。存储指数 = 0 + 127 = 127。二进制为 01111111。尾数 (M): 1.0 的尾数部分为 0。二进制为 00000000000000000000000。1.0 的 FP32 二进制表示为: \[\underbrace{0}_{\text{S}} \underbrace{01111111}_{\text{E}} \underbrace{00000000000000000000000}_{\text{M}}\]
FP16 (Floating Point 16-bit) 半精度 16 位 (2 字节)。精度和范围都比 FP32 小,但计算速度快,模型体积减半。常用于加速训练和推理。
FP16 (Half-Precision) 也是 IEEE 754 标准,共 16 位,结构类似 FP32,但位数更少: \[\text{FP16} = \text{符号位 (1 位)} + \text{指数位 (5 位)} + \text{尾数位 (10 位)}\]
公式类似: \[V = (-1)^{\text{符号}} \times (1 + \text{尾数}) \times 2^{(\text{指数} - 15)}\]
其中:
符号位 (S): 1 位。指数位 (E): 5 位。偏差值 (Bias) 为 2^(5-1) - 1 = 15。尾数位 (M): 10 位。由于指数位只有 5 位,FP16 的表示大小范围比 FP32 小得多 ,这是它 量化损失 的主要来源之一。
BF16 (BFloat16) 位数同样有16 位 (2 字节)。其数据结构是 指数位 8 位(与FP32相同),尾数位 7 位。在训练中,尤其在 TPU 上,比 FP16 更稳定。
BF16 最大的优势在于它的 8 位指数位与 FP32 的 8 位指数位相同 。这意味着 BF16 能够表示的数值范围(从极小数到极大数)与 FP32 完全一样。
在训练深度学习模型时,梯度的数值有时会非常大或非常小。如果精度格式的 范围不够 ,就会发生溢出 (Overflow) 或下溢 (Underflow)。BF16 保持了 FP32 的范围,这使得训练过程中的数值稳定性非常好,更容易直接替换 FP32 使用。
它的 尾数位只有 7 位 ,导致其精度(有效数字)比 FP16 和 FP32 低很多。
INT8 (Integer 8-bit) 8 位 (1 字节)。最常用的 量化 目标格式。在模型量化中,通常使用 有符号 INT8 (SInt8) 来表示量化后的权重或激活值。相比 FP32 模型大小减小 4 倍。在精度和速度之间取得了很好的平衡,许多移动端推理引擎(如 TFLite、PyTorch Mobile)都支持高效的 INT8 推理。
整数的二进制表示比浮点数简单得多,它们没有复杂的指数和尾数结构,就是纯粹的二进制整数。
类型 位数 表示范围 (十进制) 二进制示例 无符号 (UInt8) 8 位 [0, 255] 255 = 11111111 有符号 (SInt8) 8 位 [-128, 127] 1 = 00000001, -1 = 11111111
INT4 INT4 只有 4 位,是最简化的整数形式:
类型 位数 表示范围 (十进制) 二进制示例 无符号 (UInt4) 4 位 [0, 15] 15 = 1111 有符号 (SInt4) 4 位 [-8, 7] 7 = 0111, -1 = 1111
在模型量化中,INT4 也通常使用有符号 形式。
INTx 的量化表示 关键在于,INT8 或 INT4 本身只表示一个整数 ,要表示模型中的浮点数 (如 FP32 的权重),需要一个 量化公式 来建立整数 到浮点数 的映射: \[\text{FP}_{\text{Real}} = \text{Scale} \times (\text{INT}_{\text{Quantized}} - \text{Zero Point})\]
其中:
Scale :缩放因子,一个浮点数,将整数范围映射到原始 FP32 值的范围。Zero Point :零点,一个整数,代表原始 FP32 值的 0 在整数中的位置。正是这个 Scale 和 Zero Point ,使得 INT8/INT4 能够在极小的二进制位数下,近似地表示 FP32 的大范围数值。这也就是在 Android 设备上部署模型时,能够大幅减小模型体积和提高速度的秘密。
Ollama简介 Ollama 是一个开源项目,是在本地机器上运行 LLM 的强大而友好的平台。它在 LLM 技术的复杂性与人们对可访问、可定制的人工智能体验的渴望之间架起了一座桥梁。
Ollama 的核心功能是简化下载、安装和与各种 LLM 交互的过程,使用户能够探索这些 LLM 的功能,而无需大量的专业技术知识或依赖基于云的平台。
本地执行: Ollama 支持大型语言模型的本地运行,为用户提供快速高效的人工智能处理能力。 模型定制: 有了 Ollama,您可以自由定制和制作自己的模型,使其成为专业任务的理想选择。 用户友好的界面: 该工具的设计确保了易用性,可实现快速、无障碍的设置。 跨平台兼容性: 支持 macOS、Windows 和 Linux。 借助Ollama在本地部署当今主流的开源大模型,包含llama3、gemma、qwen等(其支持的开源大模型可在library (ollama.com)中查看)
安装Ollama 在Windows和MAC平台上可以直接下载安装包进行安装,在Linux平台上可使用以下命令安装:
curl -fsSL https://ollama.com/install.sh | sh
完毕之后可以输入验证:
我是直接在Windows平台上安装的,安装过程比较简单,下载安装包,打开之后直接下一步即可。默认安装在C盘,且自动配置了环境变量,可以直接在cmd里使用 ollama 命令。Ollama默认安装路径为
C:\Users%username%\AppData\Local\Programs\Ollama
如果需要转移到其他盘,安装完毕之后,也可以直接把整个文件夹剪切到其他盘。然后找到ollama自己添加的 PATH 环境变量,将其改为新的地址。
大模型存储地址修改 Ollama 默认下载的大模型存储位置也在C盘,我们需要让其下载到其他地址,也可以自己新建 OLLAMA_MODELS 环境变量,然后将其指向其他地址。
拉取的时候就会自动存储在这个地址下。
Ollama命令行使用 查看本地大模型列表:
C:\Users\stephen>ollama list
NAME ID SIZE MODIFIED
deepseek-coder-v2:16b 63fb193b3a9b 8.9 GB 32 hours ago
deepseek-r1:14b ea35dfe18182 9.0 GB 2 days ago
移除本地大模型:
ollama rm deepseek-r1:14b
创建自定义模型:
ollama create my-model -f my-model.modelfile
启动模型:
停止模型:
更新模型
C:\Users\stephen>ollama pull deepseek-r1:14b
pulling manifest
pulling 6e9f90f02bb3... 100% ▕███████████████▏ 9.0 GB
pulling 369ca498f347... 100% ▕███████████████▏ 387 B
pulling 6e4c38e1172f... 100% ▕███████████████▏ 1.1 KB
pulling f4d24e9138dd... 100% ▕███████████████▏ 148 B
pulling 3c24b0c80794... 100% ▕███████████████▏ 488 B
verifying sha256 digest
writing manifest
success
显示模型信息:
C:\Users\stephen>ollama show deepseek-coder-v2:16b
Model
architecture deepseek2
parameters 15.7B
context length 163840
embedding length 2048
quantization Q4_0
Parameters
stop "User:"
stop "Assistant:"
License
DEEPSEEK LICENSE AGREEMENT
Version 1.0, 23 October 2023
拉取deepseek-r1 拉取模型的过程极致的简单,只需要执行以下命令即可:
ollama run deepseek-r1:14b
末尾是指定的训练参数大小, deepseek 提供了7b,14b,32b等等选项。
14b大小为9G,我体验的话下载应该是无限速,中途下载速度如果变慢了,可以Ctrl C掐断后,立即重新开始,就会重置下载速度,也不会断传。
拉取完整性检验完毕之后,会直接打开deepseek的对话命令行,可以直接跟其进行交互。使用Ctrl D可以退出对话。
C:\Users\stephen>ollama run deepseek-r1:14b
>>> 介绍一下你自己
<think>
</think>
您好!我是由中国的深度求索(DeepSeek)公司开发的智能助手DeepSeek-R1。如您有任何任何问题,我会尽我所能为您提供帮助。
测试一个简单的Python编程需求:
>>> 使用python怎么执行本地命令行
<think>
嗯,用户问我“使用python怎么执行本地命令行”。这看起来是一个关于Python编程的问题,具体涉及到如何在Python中执行本地的
命令行指令。
首先,我需要理解用户的需求。他可能想要在自己的Python脚本中运行一些系统命令,比如ls、cd或者其他任何可以在终端中运行的
命令。这可能是因为他在进行自动化任务,或者想让脚本执行一些依赖于系统命令的操作。
接下来,我要考虑有哪些Python库可以用来执行命令行指令。我知道有几个常用的模块,比如os和subprocess。这两个模块都可以用
来调用外部程序,并且能够获取它们的输出或错误信息。
对于os模块来说,它有一个system()函数,可以直接运行命令,但返回的结果比较有限,主要是用于执行命令本身。而subprocess模
块则更为强大,因为它不仅可以运行命令,还可以捕捉标准输出和错误输出,处理进程的终止等等。
我需要决定推荐哪个库更好。考虑到功能性和灵活性,subprocess模块可能更适合大多数情况,尤其是当用户需要捕获命令的输出或
者处理更复杂的任务时。然而,os.system()在简单的场景下使用起来更为简单直观。
另外,我还需要考虑用户可能的使用场景。如果他只是想运行一个简单的命令,并不需要获取输出或错误信息,那么os.system()可
能足够了。但如果他需要更多的控制和反馈,比如处理返回值或者错误情况,subprocess会是更好的选择。
我应该提供两种方法的例子,让用户可以根据自己的需求来选择。这样既展示了基本的使用方法,也提供了更高级的功能实现。
此外,我还应该强调最佳实践的重要性。例如,在执行外部命令时,使用shell=True可能会带来一定的安全风险,比如命令注射攻击
。因此,如果可能的话,建议用户通过传递参数列表的方式调用命令,而不是直接拼接字符串。这样可以减少潜在的安全漏洞。
最后,我要确保解释清晰易懂,避免过于技术化的术语,让用户能够轻松理解并应用这些方法到自己的项目中。
</think>
在 Python 中,如果你想执行本地的命令行指令(例如 ls, cd, echo 等),可以通过以下几种方式实现。以下是常用的方法
:
1. 使用 os.system()
os 模块提供了一个简单的方法来执行系统命令。
示例代码:
import os
# 执行 "dir" 命令(Windows)或 "ls" 命令(Linux/macOS)
os.system("dir") # Windows
# 或者
os.system("ls") # Linux/macOS
输出:
这会直接在终端中执行命令,并输出结果到标准输出。
2. 使用 subprocess 模块
subprocess 是更强大和灵活的模块,推荐用于复杂的任务。它允许你捕捉输出、处理错误以及管理进程。
示例代码(运行命令并获取输出):
import subprocess
# 执行 "ls" 命令,并将结果存储在变量中
result = subprocess.run("ls", capture_output=True, text=True)
print(result.stdout) # 输出命令的 stdout
更复杂的用法:
import subprocess
# 使用 shell=True 可以执行更复杂的命令(不推荐用于外部输入,有安全风险)
result = subprocess.run(
"echo Hello World",
shell=True,
capture_output=True,
text=True
)
print(result.stdout) # 输出 "Hello World"
3. 使用 os.popen()
os.popen() 可以打开一个管道,方便地读取命令的输出。
示例代码:
import os
# 执行命令并获取输出
output = os.popen("ls").read()
print(output)
注意事项
安全性:如果使用 subprocess.run() 的 shell=True,可能会带来安全风险(例如命令注入攻击)。因此,在处理用户输入时,尽量避免这种方式。
平台兼容性:某些命令可能只在特定平台上可用。例如,ls 是 Unix 系统的命令,而 dir 是 Windows 的命令。
总结
如果需要简单的命令执行,可以使用 os.system()。
如果需要更灵活和强大的功能(比如捕获输出、处理错误),推荐使用 subprocess 模块。
希望这些方法能帮到你!
安装Open WebUI 手动安装wsl 我的电脑是win10企业版,没有微软商店,也不带wsl子系统,需要手动安装。可以直接参考微软的官方文档。
首先启用两个功能,使用 管理员权限 打开power shell。
启用适用于 Linux 的 Windows 子系统: dism.exe /online /enable-feature /featurename:Microsoft-Windows-Subsystem-Linux /all /norestart
启用虚拟机平台: dism.exe /online /enable-feature /featurename:VirtualMachinePlatform /all /norestart
然后重启电脑。
下载 Linux 内核更新包
安装完成后,将wsl2设为默认版本:
wsl --set-default-version 2
安装Docker 使用 Docker 来部署运行 Open WebUI 是一种简单而有效的方法,可以用一个交互友好的界面来使用Deepseek。
docker pull ghcr.io/open-webui/open-webui:main
下载完毕之后,在运行该项目前请确保部署在 Ollama 中的语言模型处于运行状态。
然后在Docker中的Terminal终端中输入并执行以下命令:
docker run -d -p 3000:8080 --add-host=host.docker.internal:host-gateway -v open-webui:/app/backend/data --name open-webui --restart always ghcr.io/open-webui/open-webui:main
启动成功后,也可以通过Docker Desktop来进行管理:
打开浏览器,转到 http://localhost:3000/ ,进行聊天测试。初次进入需要设置 管理员账户 ,在后台就可以对模型的访问进行一系列的设置。
内网穿透出去 如果想在公司内部小范围使用,或者不在电脑边,想使用手机访问deepseek,可以使用内网穿透工具,这里推荐使用 cpolar 。
cpolar官网地址: https://www.cpolar.com
注册账号,登录后,选择免费套餐,下载 cpolar 安装包,下载完毕打开,一直点下一步即可。
安装完毕后,浏览器打开本地localhost的 9200 端口:
使用自己刚刚注册的账号登录之后,在cpolar左侧导航栏中,点击 隧道管理 ,然后点击 添加隧道 ,选择 HTTP 协议,本地地址设置为 OpenWebUI 的 3000 端口
配置完成之后,点击 创建 ,等待cpolar分配一个域名。
然后点击 状态 ,里面有一个 在线隧道列表 将显示的域名复制到浏览器中,打开即可。
需要注意的是,刚才创建的是随机地址,24小时会发生变化。另外它的网址是由随机字符生成,不容易记忆。如果想把域名变成固定的二级子域名,并且不想每次都重新创建隧道来访问Open WebUI,我们可以选择创建一个固定的公网地址来解决这个问题。想要创建保留域名,需要开通Cpolar的会员,这个后面再看看。
Open WebUI的用户配置 使用外部的公共链接,首次打开后,发现没有注册新用户账号的地方,只能登录管理员账号使用,这是因为Open WebUI默认是不允许用户注册的。
探索之后发现,可以先使用oi的管理员账户登录,然后在设置里面找到,开启允许新用户注册:
或者直接在管理员后台,像下面这样点加号手动创建几个新账号来使用:
最后将对应模型的可见性设置为public公开,让非管理员用户也可以使用:
配置完成测试,使用普通账号登录之后,可以正常使用模型了,就像下面这样:
使用Python调用Deepseek的能力 对于程序开发来说,如果只是在用户层面使用UI交互,那局限性太大了,能不能使用AI的能力,来优化一些程序运行结果呢?
最近做了一个翻译的小项目,将本地的中文的 strings.xml 翻译成英文的,输出到项目中集成,完成英文界面的显示需要。
目前是用本地词条数据库加上百度,网易,阿里的翻译api来实现的,但是有一个问题,就是机器翻译的结果不是很准确,所以想能不能使用 Deepseek 来优化一下。
github发现 ollama 有官方的 Python 库了.
https://github.com/ollama/ollama-python
导入之后,可以直接使用 chat 接口调用到本地部署的模型的能力。配置好model名称,再输入 message 即可。
官方样例 from ollama import chat
from ollama import ChatResponse
response : ChatResponse = chat ( model = 'llama3.2' , messages = [
{
'role' : 'user' ,
'content' : 'Why is the sky blue?' ,
},
])
print ( response [ 'message' ][ 'content' ])
# or access fields directly from the response object
print ( response . message . content )
运行结果:
The sky appears blue because of a phenomenon called Rayleigh scattering. When sunlight reaches Earth’s atmosphere, it is made up of many different colors, each with different wavelengths. The shorter wavelengths, such as blue and violet light, are scattered in all directions by the gases and small particles in the atmosphere. Since our eyes are more sensitive to blue than violet, we perceive the sky as blue. During sunrise or sunset, the sun is closer to the horizon, so the light has to pass through more atmosphere, scattering out the shorter wavelengths and allowing the longer red and orange wavelengths to dominate, creating the colorful skies during these times.
本地翻译项目测试 import ollama
def translate_test ():
res = ollama . chat ( model = 'deepseek-r1:14b' , stream = False ,
messages = [{ 'role' : 'user' ,
'content' : '假如你是一个汽车领域的翻译专家,帮我翻译下面的几个词条:驾驶模式,智能驾驶,座椅加热,语音助手' }])
print ( res [ 'message' ][ 'content' ])
translate_test ()
结果打印:
当然可以!以下是这几个词条的翻译:
1. 驾驶模式 - Driving Mode
2. 智能驾驶 - Intelligent Driving
3. 座椅加热 - Heated Seats
4. 语音助手 - Voice Assistant
这些翻译在汽车领域中是常见的表达方式,希望对你有帮助!
可以看到使用 deepseek 的翻译质量上比在线的机器翻译要好上不少。
但是还需要将 AI 的回复进行二次处理,才能得到最终的结果,结合到程序流程中去。输出处理后的格式一旦对不上,程序的运行流程就会出错。目前仅仅是验证了一下可行性,还未正式使用。
流式输出 除了同步返回外,也支持流式输出:
from ollama import chat
stream = chat (
model = 'llama3.2' ,
messages = [{ 'role' : 'user' , 'content' : 'Why is the sky blue?' }],
stream = True ,
)
for chunk in stream :
print ( chunk [ 'message' ][ 'content' ], end = '' , flush = True )
结果打印:
<think>
</think>
The sky appears blue due to a phenomenon known as Rayleigh scattering. When sunlight reaches Earth's atmosphere, it interacts with molecules and small particles in the air. Sunlight is composed of various colors, each corresponding to different wavelengths. Blue light has a shorter wavelength and is scattered more by these tiny particles, whereas other colors like red or orange are scattered less. As a result, blue light is dispersed across the sky, making it appear blue to our eyes. This scattering effect is named after Lord Rayleigh, who explained it in the 19th century.
Process finished with exit code 0
异步请求 最后介绍下ollama库的异步请求。
AsyncClient 类用于发出异步请求。它可以配置与客户端类相同的字段。
import asyncio
from ollama import AsyncClient
async def chat ():
message = { 'role' : 'user' , 'content' : 'Why is the sky blue?' }
response = await AsyncClient (). chat ( model = 'llama3.2' , messages = [ message ])
asyncio . run ( chat ())
设置 stream=True 会修改函数,使其返回 Python 异步生成器:
import asyncio
from ollama import AsyncClient
async def chat ():
message = { 'role' : 'user' , 'content' : 'Why is the sky blue?' }
async for part in await AsyncClient (). chat ( model = 'llama3.2' , messages = [ message ], stream = True ):
print ( part [ 'message' ][ 'content' ], end = '' , flush = True )
asyncio . run ( chat ())
以上就是对 ollama-python 库的简要使用介绍。
云端服务 API 参数含义 在使用Deepseek和Kimi等厂商提供的云端大模型服务时,在api文档中,可以看到请求的参数有很多。这些常见的参数代表什么含义呢?
举例:
curl -L -X POST 'https://api.deepseek.com/chat/completions' \
-H 'Content-Type: application/json' \
-H 'Accept: application/json' \
-H 'Authorization: Bearer <TOKEN>' \
--data-raw '{
"messages": [
{
"content": "You are a helpful assistant",
"role": "system"
},
{
"content": "Hi",
"role": "user"
}
],
"model": "deepseek-chat",
"frequency_penalty": 0,
"max_tokens": 4096,
"presence_penalty": 0,
"response_format": {
"type": "text"
},
"stop": null,
"stream": false,
"stream_options": null,
"temperature": 1,
"top_p": 1,
"tools": null,
"tool_choice": "none",
"logprobs": false,
"top_logprobs": null
}'
messages - 消息列表,每个消息包含角色(role)和内容(content)。角色可以是 “system”、”user” 或 “assistant”。model - 模型名称,例如 “deepseek-chat”。frequency_penalty - 频率惩罚,用于控制模型生成重复内容的程度。介于 -2.0 和 2.0 之间的数字。如果该值为正,那么新 token 会根据其在已有文本中的出现频率受到相应的惩罚,降低模型重复相同内容的可能性。即值越高,模型越倾向于生成不同的内容。max_tokens - 最大的token数量,用于限制模型生成的响应长度。presence_penalty - 存在惩罚,用于控制模型生成新内容的程度。值越高,模型越倾向于生成新的内容。response_format - 响应格式,例如 “text” 或 “json”。stop - 停止序列,用于指定模型在生成响应时何时停止。可以是一个字符串或字符串列表。stream - 是否流式输出,默认为 false。如果设置为 True,将会以 SSE(server-sent events)的形式以流式发送消息增量。消息流以 data: [DONE] 结尾。temperature - 采样温度,介于 0 和 2 之间。更高的值,如 0.8,会使输出更随机,而更低的值,如 0.2,会使其更加集中和确定。 我们通常建议可以更改这个值或者更改 top_p,但不建议同时对两者进行修改。top_p - nucleus sampling 概率阈值,介于 0 和 1 之间。模型会根据其概率分布生成下一个 token,而 top_p 则会限制模型只考虑概率最高的前 p% 的 token。例如设置为 0.1 就意味着只有包括在最高 10% 概率中的 token 会被考虑。tools - 工具列表,用于指定模型可能会调用的 tool 的列表。目前,仅支持 function 作为工具。使用此参数来提供以 JSON 作为输入参数的 function 列表。最多支持 128 个 function。tool_choice - 工具选择,用于指定模型应该使用哪个工具。可以是 “none”、”auto” 或工具名称。logprobs - logprobs 参数让你可以查看模型在生成每个词(token)时,它认为各个候选词的“可能性”有多大,并以一种数学上更优的形式——对数概率——返回给你。如果为 true,则在 message 的 content 中返回每个输出 token 的对数概率。temperature和top_p实现调控的区别 temperature temperature 像一个“软化剂 ”或“锐化剂 ”,它直接作用于所有词语的概率分布。
值越高 (比如 1.0): 它会“软化” 概率分布,让那些本来概率很低的词语(比如“桌子”的 5%)的权重提高,变得更有可能被选中。这样模型的选择范围就扩大了,输出会更加随机和有创意。值越低 (比如 0.2): 它会“锐化” 概率分布,让高概率的词语(比如“苹果”的 50%)的权重更加突出。模型会更倾向于选择最安全、最确定的词语,输出会更保守、更重复。改变 temperature 就像是在调整整个概率曲线的形状 ,影响了所有词语被选中的相对可能性。
top_p top_p 则是一个“概率预算 ”,它通过限制可选词语的数量 来控制随机性。
模型会按概率从高到低排序,然后选择一个最小的词语集合,使得这些词语的累积概率达到你设置的 top_p 值。模型后续的选择只会从这个被“裁剪”的集合中进行。如果你设置 top_p=0.9,模型会选出那些加起来概率达到 90% 的词语,将完全排除概率很低的词语。
值越高 (比如 0.9): 预算更大,模型可选的词语更多,输出更多样。值越低 (比如 0.1): 预算很小,模型只能选择最有可能的少数几个词,输出更保守。改变 top_p 就像是在概率列表上画一条线 ,直接淘汰掉那些累积概率达不到预算的词语。
调参的经验法则 对于需要事实准确、代码或总结 的严谨任务,将 temperature 设置为 0.0 到 0.5 左右top_p 设置为 0.95 或更高
对于需要创意、故事或头脑风暴 的任务,将 temperature 设置为 0.7 到 1.0 左右top_p 设置为 0.8 到 0.9
滑动窗口其实也可以归类为双指针的一种。滑动窗口的基本思想是维护一个窗口,窗口内的元素满足某些条件。窗口的左右边界分别用两个指针表示,窗口的大小可以变化。
解题通用模板:
//外层循环扩展右边界,内层循环扩展左边界
for ( int l = 0 , r = 0 ; r < n ; r ++ ) {
//当前考虑的元素
while ( l <= r && check ()) { //区间[left,right]不符合题意
//扩展左边界
}
//区间[left,right]符合题意,统计相关信息
}
长度最小的子数组 209. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其总和大于等于 target 的长度最小的 子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
提示:
1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 104
进阶:
如果你已经实现 O(n) 时间复杂度的解法, 请尝试设计一个 O(n log(n)) 时间复杂度的解法。
暴力解法 暴力解法的思路是枚举所有可能的子数组,计算子数组的和是否大于等于target。如果是,更新最小长度。
class Solution {
public int minSubArrayLen ( int s , int [] nums ) {
int n = nums . length ;
if ( n == 0 ) {
return 0 ;
}
int ans = Integer . MAX_VALUE ;
// 枚举子数组的左边界
for ( int i = 0 ; i < n ; i ++ ) {
int sum = 0 ;
// 枚举子数组的右边界
for ( int j = i ; j < n ; j ++ ) {
sum += nums [ j ];
if ( sum >= s ) {
ans = Math . min ( ans , j - i + 1 );
break ;
}
}
}
return ans == Integer . MAX_VALUE ? 0 : ans ;
}
}
复杂度分析
时间复杂度:O(n2),其中 n 是数组的长度。需要遍历每个下标作为子数组的开始下标,对于每个开始下标,需要遍历其后面的下标得到长度最小的子数组。 空间复杂度:O(1)。 滑动窗口 滑动窗口的思路是维护一个窗口,窗口的左右边界分别用两个指针表示,窗口的大小可以变化。
初始时,窗口的左右边界都指向数组的第一个元素,sum和设为0。
每次将右指针右移一位,将右指针指向的元素加入sum中。 如果sum大于等于target,说明满足条件了,更新最小长度,同时将左指针右移一位,将左指针指向的元素从sum中减去。 重复以上步骤,直到右指针到达数组的末尾。 class Solution {
public:
int minSubArrayLen ( int s , vector < int >& nums ) {
int n = nums . size ();
if ( n == 0 ) {
return 0 ;
}
// 因为要找最小值,result设为 INT_MAX 最大值,方便后续比较
int result = INT_MAX ;
int left = 0 ;
int right = 0 ;
int sum = 0 ;
// 右指针右移,加入元素
while ( right <= n - 1 ) {
sum += nums [ right ];
// 可以不用判断左右指针相对位置,重合时,减完sum就为0了
while ( sum >= s ) {
result = min ( right - left + 1 , result );
// 左指针右移,提前减去这个位置的元素
sum -= nums [ left ];
left ++ ;
}
right ++ ;
}
// 如果result没有被更新,说明没有符合条件的子数组
return result == INT_MAX ? 0 : result ;
}
};
无重复字符的最长子串 3. 无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长 子串 的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
提示:
0 <= s.length <= 5 * 104
s 由英文字母、数字、符号和空格组成
滑动窗口加unordered_set记录 我们不妨以示例一中的字符串 abcabcbb 为例,找出从每一个字符开始的,不包含重复字符的最长子串,那么其中最长的那个字符串即为答案。对于示例一中的字符串,我们列举出这些结果,其中括号中表示选中的字符以及最长的字符串:
以 (a)bcabcbb 开始的最长字符串为 (abc)abcbb;
以 a(b)cabcbb 开始的最长字符串为 a(bca)bcbb;
以 ab(c)abcbb 开始的最长字符串为 ab(cab)cbb;
以 abc(a)bcbb 开始的最长字符串为 abc(abc)bb;
以 abca(b)cbb 开始的最长字符串为 abca(bc)bb;
以 abcab(c)bb 开始的最长字符串为 abcab(cb)b;
以 abcabc(b)b 开始的最长字符串为 abcabc(b)b;
以 abcabcb(b) 开始的最长字符串为 abcabcb(b)。
可以看到,随着左指针移动,右边界也是在移动的。
我们就可以使用「滑动窗口」来解决这个问题了:
我们使用两个指针表示字符串中的某个子串(或窗口)的左右边界,其中左指针代表着上文中「枚举子串的起始位置」。
在每一步的操作中,我们会将左指针向右移动一格,表示 我们开始枚举下一个字符作为起始位置,然后我们可以不断地向右移动右指针,但需要保证这两个指针对应的子串中没有重复的字符。在移动结束后,这个子串就对应着 以左指针开始的,不包含重复字符的最长子串。我们记录下这个子串的长度;
在枚举结束后,我们找到的最长的子串的长度即为答案。
class Solution {
public:
int lengthOfLongestSubstring ( string s ) {
int n = s . size ();
if ( n <= 1 ) {
return n ;
}
int ans = 0 ;
unordered_set < char > filter ;
int right = 0 ;
for ( int left = 0 ; left < n ; left ++ ) {
// 左指针向右移动一格,移除掉遍历检查过的字符
if ( left != 0 ) {
// 移除掉遍历检查过的字符
filter . erase ( s [ left - 1 ]);
}
// 右指针向右移动,加入元素,直到遇到重复元素
while ( right <= n - 1 && ! filter . count ( s [ right ])) {
filter . insert ( s [ right ]);
right ++ ;
}
// 更新答案,此时右指针指向的元素是重复元素,所以 right - left 是当前窗口的长度
ans = max ( ans , right - left );
}
return ans ;
}
};
438.找到字符串中所有字母异位词 438. 找到字符串中所有字母异位词
给定两个字符串 s 和 p,找到 s 中所有 p 的 异位词 的子串,返回这些子串的起始索引。不考虑答案输出的顺序。
示例 1:
输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。
示例 2:
输入: s = "abab", p = "ab"
输出: [0,1,2]
解释:
起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。
起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。
起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。
提示:
1 <= s.length, p.length <= 3 * 104
s 和 p 仅包含小写字母
思路 滑动窗口检查异位词 根据题目要求,我们需要在字符串 s 寻找字符串 p 的异位词。因为字符串 p 的异位词的长度一定与字符串 p 的长度相同,所以我们可以在字符串 s 中构造一个长度为与字符串 p 的长度相同的滑动窗口 ,并在滑动中维护窗口中每种字母的数量 ;
不需要费劲去排列组合,只需要看每种字符的数量是否相等即可。
当窗口中每种字母的数量与字符串 p 中每种字母的数量相同时,则说明当前窗口为字符串 p 的异位词。
而且字符的存储形式是一个整形,所以我们可以用一个 vector<int> 来记录窗口中每种字母的数量。
两个 vector<int> 分别记录字符串 p 中每种字母的数量和窗口中每种字母的数量。数组相等可以直接使用 == 运算符。底层已经实现了。
vector 的 == 运算符,内部已实现,先判断长度,若长度相同再逐个比较元素是否相等。
class Solution {
public:
vector < int > findAnagrams ( string s , string p ) {
int sSize = s . size ();
int pSize = p . size ();
if ( sSize < pSize ) {
return {};
}
vector < int > result ;
// 承载s和p中每一个字符的数组,大小固定为26
vector < int > sDict ( 26 );
vector < int > pDict ( 26 );
for ( int i = 0 ; i < pSize ; i ++ ) {
// 填入字母和字符a的差值作为存储判断的数据
sDict [ s [ i ] - 'a' ] ++ ;
pDict [ p [ i ] - 'a' ] ++ ;
}
// 至此,p字符串的结构体已经录入了pDict这个数组
// 先比较一次s的开头字符串
if ( sDict == pDict ) {
result . emplace_back ( 0 );
}
// 比较剩余的元素
for ( int i = 0 ; i < sSize - pSize ; i ++ ) {
// 补上新的剩余字符计入
sDict [ s [ pSize + i ] - 'a' ] ++ ;
// 删掉之前计算的字符,保持窗口大小不变
sDict [ s [ i ] - 'a' ] -- ;
if ( sDict == pDict ) {
// i 是从减去p长度的后一个位置开始的,在s中的实际下标需要加 1
result . emplace_back ( i + 1 );
}
}
return result ;
}
};
emplace_back 是 vector 的一个成员函数,用于在 vector 的末尾直接构造一个元素,而不是先创建一个临时对象再将其复制到 vector 中。适合大对象,复杂对象的构造。这里使用 push_back 也没差。
30.串联所有单词的子串 30. 串联所有单词的子串
这题可以说是438的进阶版,不过一个是字符,一个是字符串版本。
给定一个字符串 s 和一个字符串数组 words。 words 中所有字符串 长度相同。
s 中的 串联子串 是指一个包含 words 中所有字符串以任意顺序排列连接起来的子串。
例如,如果 words = ["ab","cd","ef"], 那么 "abcdef", "abefcd","cdabef", "cdefab","efabcd", 和 "efcdab" 都是串联子串。 "acdbef" 不是串联子串,因为他不是任何 words 排列的连接。
返回所有串联子串在 s 中的开始索引。你可以以 任意顺序 返回答案。
示例 1:
输入:s = "barfoothefoobarman", words = ["foo","bar"]
输出:[0,9]
解释:因为 words.length == 2 同时 words[i].length == 3,连接的子字符串的长度必须为 6。
子串 "barfoo" 开始位置是 0。它是 words 中以 ["bar","foo"] 顺序排列的连接。
子串 "foobar" 开始位置是 9。它是 words 中以 ["foo","bar"] 顺序排列的连接。
输出顺序无关紧要。返回 [9,0] 也是可以的。
示例 2:
输入:s = "wordgoodgoodgoodbestword", words = ["word","good","best","word"]
输出:[]
解释:因为 words.length == 4 并且 words[i].length == 4,所以串联子串的长度必须为 16。
s 中没有子串长度为 16 并且等于 words 的任何顺序排列的连接。
所以我们返回一个空数组。
示例 3:
输入:s = "barfoofoobarthefoobarman", words = ["bar","foo","the"]
输出:[6,9,12]
解释:因为 words.length == 3 并且 words[i].length == 3,所以串联子串的长度必须为 9。
子串 "foobarthe" 开始位置是 6。它是 words 中以 ["foo","bar","the"] 顺序排列的连接。
子串 "barthefoo" 开始位置是 9。它是 words 中以 ["bar","the","foo"] 顺序排列的连接。
子串 "thefoobar" 开始位置是 12。它是 words 中以 ["the","foo","bar"] 顺序排列的连接。
提示:
1 <= s.length <= 104
1 <= words.length <= 5000
1 <= words[i].length <= 30
words[i] 和 s 由小写英文字母组成
滑动窗口检查 使用的还是滑动窗口检查异位词这题的思想。只不过检查的对象成了字符串,并且用来比较的数据集合改用hash表,记录每个字符串出现的次数。
重点在于如何划分窗口。记 words 的长度为 m ,words 中每个单词的长度为 n , s 的长度为 ls 。首先需要将 s 划分为单词组,每个单词的大小均为 n (首尾除外)。这样的划分方法有 n 种,即先删去前 i (i=0∼n−1) 个字母后,将剩下的字母进行划分,如果末尾有不到 n 个字母也删去。对这 n 种划分得到的单词数组分别使用滑动窗口对 words 进行类似于字母异位词的搜寻。
检查流程如下:
第一次滑动流程
初始窗口 ['bar', 'foo','foo'] 未命中
入'bar'出'bar' ['foo','foo','bar'] 未命中
入'the'出'foo' ['foo','bar', 'the'] 命中 index 6
入'foo'出'foo' ['bar','the', 'foo'] 命中 index 9
入'bar'出'bar' ['the','foo','bar'] 命中index 12
入'man'出'the' ['foo','bar','man'] 未命中
结束
第二次滑动流程
初始窗口 ['arf','oof','oob'] 未命中
划动过程略
第三次滑动流程
初始窗口 ['rfo','ofo','oba'] 未命中
划动过程略
class Solution {
public:
vector < int > findSubstring ( string & s , vector < string >& words ) {
vector < int > res ; // 存储结果的向量,记录所有符合条件的起始索引
// 获取关键参数:
int m = words . size (); // words中单词的个数
int n = words [ 0 ]. size (); // 每个单词的长度(题目保证所有单词长度相同)
int ls = s . size (); // 字符串s的长度
// 外层循环:从0到n-1,处理不同的起始偏移量
// 这样可以覆盖所有可能的对齐方式
// 第二个结束条件就是剩余的字符串长度不足以支持分割
for ( int i = 0 ; i < n && i + m * n <= ls ; ++ i ) {
// 使用哈希表记录当前窗口内各单词出现次数与words中次数的差异
unordered_map < string , int > differ ;
// 初始化滑动窗口:截取从位置i开始的m个单词
for ( int j = 0 ; j < m ; ++ j ) {
// 从s中截取一个单词并加入differ(增加计数)
++ differ [ s . substr ( i + j * n , n )];
}
// 用words中的单词来平衡differ(减少计数)
for ( string & word : words ) {
// 如果某个单词在words中,就在differ中减少其计数
if ( -- differ [ word ] == 0 ) {
// 如果计数减到0,就从differ中移除该单词
differ . erase ( word );
}
}
// 开始逐词滑动窗口遍历
for ( int start = i ; start < ls - m * n + 1 ; start += n ) {
// 初始窗口第一次检查已完成,如果不是初始窗口,需要更新differ
if ( start != i ) {
// 添加新进入窗口的单词(窗口右边界新增的单词)
string word = s . substr ( start + ( m - 1 ) * n , n );
if ( ++ differ [ word ] == 0 ) {
differ . erase ( word ); // 如果计数变为0,移除
}
// 移除离开窗口的单词(窗口左边界移出的单词)
word = s . substr ( start - n , n );
if ( -- differ [ word ] == 0 ) {
differ . erase ( word ); // 如果计数变为0,移除
}
}
// 检查当前窗口是否匹配:如果differ为空,说明窗口内的单词与words完全匹配
if ( differ . empty ()) {
res . emplace_back ( start ); // 记录当前起始位置
}
}
}
return res ; // 返回所有找到的起始索引
}
};
76.最小覆盖子串 76. 最小覆盖子串
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:
对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串,我们保证它是唯一的答案。
示例 1:
输入:s = "ADOBECODEBANC", t = "ABC"
输出:"BANC"
解释:最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。
示例 2:
输入:s = "a", t = "a"
输出:"a"
解释:整个字符串 s 是最小覆盖子串。
示例 3:
输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中,
因此没有符合条件的子字符串,返回空字符串。
提示:
m == s.length
n == t.length
1 <= m, n <= 105
s 和 t 由英文字母组成
进阶:你能设计一个在 o(m+n) 时间内解决此问题的算法吗?
滑动窗口加哈希表动态判断 解题思路,右指针往前遍历,一路扩大检查的范围,直到当前窗口区域内,可以包含 t 字符串的组成字符数量后,再缩小范围,直到不包含,过程中动态更新区间大小,取最短区间。
本地验证OK,问题点是添加了一个hash表来判断对比,超出内存限制了。
class Solution {
public:
bool checkDict ( unordered_map < char , int >& dyDict ,
unordered_map < char , int >& tDict ) {
auto it = tDict . begin ();
while ( it != tDict . end ()) {
if ( it -> second > dyDict [ it -> first ]) {
return false ;
}
it ++ ;
}
return true ;
}
string minWindow ( string s , string t ) {
int n = s . size ();
int m = t . size ();
if ( n < m ) {
return "" ;
}
// 需要动态更新最小值
string result = "" ;
bool isFound = false ;
unordered_map < char , int > tDict ;
unordered_map < char , int > dynamicDitct ;
// 先填入即将用来比对hash表数据
for ( char c : t ) {
tDict [ c ] ++ ;
}
// 思路,一路扩大检查的范围,直到包含的tDict中的字符数量后,再缩小范围到不包含,记录下区间大小
int right = 0 ;
int left = 0 ;
while ( right < n ) {
dynamicDitct [ s [ right ]] ++ ;
// 包含了组成t的字符组合
while ( left < n && left + m <= right + 1 &&
checkDict ( dynamicDitct , tDict )) {
string temp = s . substr ( left , right - left + 1 );
if ( result == "" ) {
result = temp ;
} else {
result = result . size () > temp . size () ? temp : result ;
}
dynamicDitct [ s [ left ]] -- ;
left ++ ;
}
right ++ ;
}
return result ;
}
};
优化内存消耗 内存问题有以下几点:
每次检查都要遍历整个 tDict ,在滑动窗口过程中被调用次数为 O(n²) 级别 每次调用 dyDict[it->first] 可能会在 dyDict 中创建新键值对 频繁截取字符串,字符串可能很长,频繁创建和销毁消耗大量内存 优化思路:
使用两个计数器 required 和 formed 来跟踪需要匹配的字符种类数和当前已匹配的字符种类数,避免每次都遍历整个 tDict class Solution {
public:
string minWindow ( string s , string t ) {
if ( s . empty () || t . empty () || s . length () < t . length ()) return "" ;
unordered_map < char , int > tCount ;
for ( char c : t ) tCount [ c ] ++ ;
int required = tCount . size (); // 需要匹配的字符种类数
int formed = 0 ; // 当前已匹配的字符种类数
unordered_map < char , int > windowCount ;
int left = 0 , right = 0 ;
int minLen = INT_MAX ;
int start = 0 ;
while ( right < s . length ()) {
char c = s [ right ];
windowCount [ c ] ++ ;
// 检查当前字符是否达到t中的要求
if ( tCount . count ( c ) && windowCount [ c ] == tCount [ c ]) {
formed ++ ;
}
// 尝试收缩窗口
while ( left <= right && formed == required ) {
c = s [ left ];
// 更新最小窗口
if ( right - left + 1 < minLen ) {
minLen = right - left + 1 ;
start = left ;
}
// 移动左指针
windowCount [ c ] -- ;
if ( tCount . count ( c ) && windowCount [ c ] < tCount [ c ]) {
formed -- ;
}
left ++ ;
}
right ++ ;
}
return minLen == INT_MAX ? "" : s . substr ( start , minLen );
}
};
官方题解 思路相同,性能更优:
class Solution {
public:
unordered_map < char , int > ori , cnt ;
bool check () {
for ( const auto & p : ori ) {
if ( cnt [ p . first ] < p . second ) {
return false ;
}
}
return true ;
}
string minWindow ( string s , string t ) {
for ( const auto & c : t ) {
++ ori [ c ];
}
int l = 0 , r = - 1 ;
int len = INT_MAX , ansL = - 1 , ansR = - 1 ;
while ( r < int ( s . size ())) {
if ( ori . find ( s [ ++ r ]) != ori . end ()) {
++ cnt [ s [ r ]];
}
while ( check () && l <= r ) {
if ( r - l + 1 < len ) {
len = r - l + 1 ;
ansL = l ;
}
if ( ori . find ( s [ l ]) != ori . end ()) {
-- cnt [ s [ l ]];
}
++ l ;
}
}
return ansL == - 1 ? string () : s . substr ( ansL , len );
}
};
由于数据特征的有序性(大小或者正负) ,所以可以证明当前节点一定是优于过往节点,从而可以通过数据的维度数量的指针,逐步的迭代收敛最终找到最优解。
无序数据大多只能通过遍历的方式来解决,因为无法通过指针的移动来证明当前节点是否是最优解。
回文字符串判断 验证回文字符串
如果在将所有大写字符转换为小写字符、并移除所有非字母数字字符之后,短语正着读和反着读都一样。则可以认为该短语是一个 回文串 。
字母和数字都属于字母数字字符。
给你一个字符串 s,如果它是 回文串 ,返回 true ;否则,返回 false 。
示例 1:
输入: s = "A man, a plan, a canal: Panama"
输出:true
解释:"amanaplanacanalpanama" 是回文串。
示例 2:
输入:s = "race a car"
输出:false
解释:"raceacar" 不是回文串。
示例 3:
输入:s = " "
输出:true
解释:在移除非字母数字字符之后,s 是一个空字符串 "" 。
由于空字符串正着反着读都一样,所以是回文串。
提示:
1 <= s.length <= 2 * 105
s 仅由可打印的 ASCII 字符组成
kotlin速通 class Solution {
fun isPalindrome ( s : String ): Boolean {
val cleanedString = s . lowercase (). replace ( Regex ( "[^a-z0-9]" ), "" )
return cleanedString == cleanedString . reversed ()
}
}
使用方便的扩展函数结合正则表达式替换,可以一两行输出结果。
思路1 使用封装好的库函数处理 去除多余字符,转换为小写,翻转,与原来的做比较:
class Solution {
public:
bool isPalindrome ( string s ) {
// 去除掉所有非字母数字的其他字符
s . erase ( remove_if ( s . begin (), s . end (),
[]( unsigned char c ) { return ! isalnum ( c ); }),
s . end ());
// 转换为小写
transform ( s . begin (), s . end (), s . begin (), :: tolower );
// 反转字符串
string reversed = s ;
reverse ( reversed . begin (), reversed . end ());
// 比较反转后的字符串是否与原字符串相同
return reversed == s ;
}
};
优化调用库函数 将字符的剔除,转换合二为一:
class Solution {
public:
bool isPalindrome ( string s ) {
string sgood ;
for ( char ch : s ) {
// 剔除非字母数字字符
if ( isalnum ( ch )) {
// 转换为小写并添加到新字符串
sgood += tolower ( ch );
}
}
// 创建翻转的字符串也可以写作下面这样
string sgood_rev ( sgood . rbegin (), sgood . rend ());
return sgood == sgood_rev ;
}
};
isalnum() 函数用于检查一个字符是否是字母或数字。类似的还有 isdigit() 判断是否是数字; isalpha() 判断是否是字母。
双指针移动比较 设置两个指针,一个指向字符串的头,一个指向字符串的尾,向中间移动,比较对应位置的字符是否相同。
需要注意的是,在移动左右指针时, 遇到非字母数字字符时,需要跳过 ,继续往下移动到下一个有效字符。
class Solution {
public:
bool isPalindrome ( string s ) {
int n = s . size ();
int left = 0 , right = n - 1 ;
while ( left < right ) {
while ( left < right && ! isalnum ( s [ left ])) {
++ left ;
}
while ( left < right && ! isalnum ( s [ right ])) {
-- right ;
}
if ( left < right ) {
if ( tolower ( s [ left ]) != tolower ( s [ right ])) {
return false ;
}
++ left ;
-- right ;
}
}
return true ;
}
};
判断子序列 判断子序列
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
进阶:
如果有大量输入的 S,称作 S1, S2, ... , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
示例 1:
输入:s = "abc", t = "ahbgdc"
输出:true
示例 2:
输入:s = "axc", t = "ahbgdc"
输出:false
提示:
0 <= s.length <= 100
0 <= t.length <= 10^4
个字符串都只由小写字符组成。
双指针移动比较 这个子字符串的定义不同于之前的连续的子字符串,它可以不连续。思路简单直接写即可,基于长串遍历,子串也从头开始移动,遇到当前长串字符和子串的字符匹配上的,就移动一下子串的指针,比较下一个字符,子串遍历完成,即为成功,如果长串走完了还没有成功,就返回失败。
class Solution {
public:
bool isSubsequence ( string s , string t ) {
int n = s . size ();
if ( n == 0 ) {
return true ;
}
int subPtr = 0 ;
for ( int i = 0 ; i < t . size (); i ++ ) {
// 有和子字符串相同的字符出现
if ( s [ subPtr ] == t [ i ]) {
// 比较下一个
subPtr ++ ;
// 子字符串遍历完成,结束
if ( subPtr == n ) {
return true ;
}
}
}
return false ;
}
};
两数之和 两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案,并且你不能使用两次相同的元素。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
提示:
2 <= nums.length <= 104
-109 <= nums[i] <= 109
-109 <= target <= 109
只会存在一个有效答案
进阶:你可以想出一个时间复杂度小于 O(n2) 的算法吗?
这题非双指针类别,但是是下一题的基础,同时也记录一下。
思路1 暴力枚举 很容易想到类似冒泡排序的写法,遍历数组,对于每个元素,都遍历数组后面的元素,看是否有和当前元素之和等于目标值的元素。
class Solution {
public:
vector < int > twoSum ( vector < int >& nums , int target ) {
int n = nums . size ();
for ( int i = 0 ; i < n ; i ++ ) {
for ( int j = i + 1 ; j < n ; j ++ ) {
if ( nums [ i ] + nums [ j ] == target ) {
return { i , j };
}
}
}
return {};
}
};
hash 表记录 上一个暴力解法的时间复杂度是 O(n2),主要是搜索差值的过程比较耗时。我们可以用 hash 表记录已经遍历过的元素,每次遍历到一个元素时,都去 hash 表中查找是否有和当前元素之和等于目标值的元素。如果有,就返回这两个元素的下标。时间复杂度为O(n).
class Solution {
public:
vector < int > twoSum ( vector < int >& nums , int target ) {
int n = nums . size ();
unordered_map < int , int > valueIndex ;
for ( int i = 0 ; i < n ; i ++ ) {
// 查看 hash 表中是否有和当前元素之和等于目标值的元素
auto it = valueIndex . find ( target - nums [ i ]);
if ( it != nullptr ) {
// 找到和为目标值的元素,返回这两个元素的下标
return { it -> second , i };
}
valueIndex [ nums [ i ]] = i ;
}
// 遍历完成,没有找到,返回空
return {};
}
};
两数之和II 输入有序数组 两数之和II 输入有序数组
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。
以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
你所设计的解决方案必须只使用常量级的额外空间。
示例 1:
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]
解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
示例 2:
输入:numbers = [2,3,4], target = 6
输出:[1,3]
解释:2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。
示例 3:
输入:numbers = [-1,0], target = -1
输出:[1,2]
解释:-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
提示:
2 <= numbers.length <= 3 * 104
-1000 <= numbers[i] <= 1000
numbers 按 非递减顺序 排列
-1000 <= target <= 1000
仅存在一个有效答案
对比第一题,要求不另外开辟空间,就只能在原数组上操作了。
同时也多了一个条件,即数组是有序的。经测试,这题如果使用暴力解法会超时。即算法时间复杂度要优于 O(n^2) .
思路1 双指针 因为数组是有序的,所以可以采用一个头一个尾,计算和值sum,与target比较,缩小范围。如果sum太小,就左指针右移,sum太大,就右指针左移。
初始时两个指针分别指向第一个元素位置和最后一个元素的位置。每次计算两个指针指向的两个元素之和,并和目标值比较。如果两个元素之和等于目标值,则发现了唯一解。如果两个元素之和小于目标值,则将左侧指针右移一位。如果两个元素之和大于目标值,则将右侧指针左移一位。移动指针之后,重复上述操作,直到找到答案。
class Solution {
public:
vector < int > twoSum ( vector < int >& numbers , int target ) {
int n = numbers . size ();
int left = 0 ;
int right = n - 1 ;
while ( right > left ) {
if ( numbers [ left ] + numbers [ right ] > target ) {
right -- ;
} else if ( numbers [ left ] + numbers [ right ] < target ) {
left ++ ;
} else {
return { left + 1 , right + 1 };
}
}
return {};
}
};
复杂度分析
时间复杂度:O(n),其中 n 是数组的长度。两个指针移动的总次数最多为 n 次。
空间复杂度:O(1)。
思路2 二分查找 在数组中找到两个数,使得它们的和等于目标值,可以首先固定第一个数,然后寻找第二个数,第二个数等于目标值减去第一个数的差。利用数组的有序性质,可以通过二分查找的方法寻找第二个数。为了避免重复寻找,在寻找第二个数时,只在第一个数的右侧寻找。
low 和 high 的移动类似双指针的解法,这里是划分区间,看target落在哪里,“击中”区间后就缩小范围寻找。
class Solution {
public:
vector < int > twoSum ( vector < int >& numbers , int target ) {
for ( int i = 0 ; i < numbers . size (); ++ i ) {
int low = i + 1 , high = numbers . size () - 1 ;
while ( low <= high ) {
int mid = ( high - low ) / 2 + low ;
if ( numbers [ mid ] == target - numbers [ i ]) {
return { i + 1 , mid + 1 };
} else if ( numbers [ mid ] > target - numbers [ i ]) {
high = mid - 1 ;
} else {
low = mid + 1 ;
}
}
}
return { - 1 , - 1 };
}
};
盛水最多的容器 盛水最多的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例1:
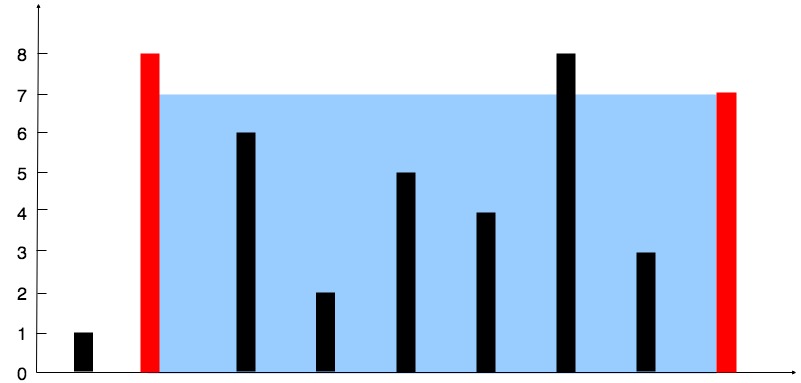
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1] 输出:1
提示: n == height.length 2 <= n <= 105 0 <= height[i] <= 104
思路1 双指针 根据图示,可以比较容易想到使用双指针,因为做区间限制计算,需要有两个下标。
设置双指针,共同从两边开始往中间移动,直到相遇,指针移动时,记录下所组合到的最大面积 (right-left)X 短的那个指针的高度 。问题点就是该移动哪一个指针。
比较通俗的想法是,移动高度比较短的那个指针,因为移动长的那个指针,容器的高度不会增加,而宽度会减少,所以容器的面积一定是减少的。数学证明也是如此,省略证明过程。
class Solution {
public:
int maxArea ( vector < int >& height ) {
int n = height . size ();
int left = 0 ;
int right = n - 1 ;
int maxArea = 0 ;
while ( left < right ) {
// 计算当前面积,更新maxArea的值
int areaHeight = min ( height [ left ], height [ right ]);
maxArea = max ( maxArea , ( right - left ) * areaHeight );
// 移动对应高度较短的那个指针
height [ left ] >= height [ right ] ? right -- : left ++ ;
}
return maxArea ;
}
};
复杂度分析
时间复杂度:O(N),双指针总计最多遍历整个数组一次。 空间复杂度:O(1),只需要额外的常数级别的空间。
三数之和 三数之和
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
示例 1:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:nums = [0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:nums = [0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
提示:
3 <= nums.length <= 3000
-105 <= nums[i] <= 105
思路1 排序加双指针 题目要求找元素组合,并未对下标做限制,所以可以先排序,然后使用双指针。可以预料到时间复杂度至少为O(N^2),而sort的时间复杂度为O(NlogN),所以整体时间复杂度为O(N^2)。
求解思路类似两数之和的双指针,只是在三数之和的基础上,增加了一个循环。遍历数组时,先锁定第一个数 numbers[i] ,再设置两个指针,一个指向较小的位置(i的下一个位置),一个指向末尾,求和,如果大于0,就将right左移,如果小于0,就将left右移,知道两个指针遇上。
关于去重:
因为数组已经排过序,所以去重时,对第一个元素去重时,需要判断当前元素和前一个元素是否相等,如果相等,就跳过。 对于left这个第二位的元素,只有当匹配上一组结果了才需要去重,去重时,要看这个元素的后面一个元素是否相等,如果相等就略过,left多往右移几位,知道下一个检查的元素不相等了。 对于right,也是只有匹配上了才去重,看看right左边的元素与其是否相等,如果相等,就略过,right多走几步。 class Solution {
public:
vector < vector < int >> threeSum ( vector < int >& nums ) {
int n = nums . size ();
// 先排序
sort ( nums . begin (), nums . end ());
vector < vector < int >> result ;
for ( int i = 0 ; i < n - 2 ; i ++ ) {
int lock = nums [ i ];
// 说明遍历到此处,后面的元素已经都大于0了
if ( lock > 0 ) {
return result ;
}
// 对第一个元素去重
if ( i > 0 && lock == nums [ i - 1 ]) {
continue ;
}
int left = i + 1 ;
int right = n - 1 ;
while ( left < right ) {
int sum = lock + nums [ left ] + nums [ right ];
if ( sum > 0 ) {
// 结果大于0,缩小right指针
right -- ;
} else if ( sum < 0 ) {
// 结果小于0,增大left指针
left ++ ;
} else {
// 添加进结果数组中
result . push_back ({ nums [ i ], nums [ left ], nums [ right ]});
// 去重逻辑应该放在找到一个三元组之后,对left和right进行多移几位的操作
while ( right > left && nums [ right ] == nums [ right - 1 ])
right -- ;
while ( right > left && nums [ left ] == nums [ left + 1 ])
left ++ ;
// 找到答案时,双指针同时收缩
right -- ;
left ++ ;
}
}
}
return result ;
}
};
移动零 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
提示:
1 <= nums.length <= 104
-231 <= nums[i] <= 231 - 1
进阶:你能尽量减少完成的操作次数吗?
思路1 双指针 朴素写法,遍历数组,遇到0,就将0后面的元素往前移动,然后将0放到数组的末尾。这是一个O(n^2)的算法。
使用双指针进行优化,一个指针指向当前遍历的元素,一个指针指向当前0的位置。当往前遍历的快指针遇到第一个非0元素时,就将这个非0元素移动到指向0的慢指针的位置。慢指针继续去找0,最后将尾部剩余空间全部写成0即可。
class Solution {
public:
void moveZeroes ( vector < int >& nums ) {
int n = nums . size ();
if ( n < 1 ) {
return ;
}
int slow = 0 ;
for ( int fast = 0 ; fast < n ; fast ++ ) {
if ( nums [ fast ] == 0 ) {
continue ;
}
nums [ slow ] = nums [ fast ];
slow ++ ;
}
for ( int i = slow ; i < n ; i ++ ) {
nums [ i ] = 0 ;
}
}
};
背景 近期决定补齐一下算法方面的知识,因为是非计算机科班出身,没有系统学过 C++数据结构和算法 这门课,在算法方面的知识很薄弱,想要从应用层往下深入就很困难。
Android 应用开发做需求时完全用不到算法,性能优化时是规避JVM内存泄漏,按照Android系统的规则来处理,相当于是在别人预设好的算法环境上来适配自己的代码。
所以打算借着刷算法题,把一些算法的实现记录下来,方便以后回顾。然后对于重难点进行系统的学习。
数组和字符串常用操作 在 C++ 算法题中,字符串(std::string)和数组(通常是 std::vector 或原生数组)是最常用的数据结构之一。熟练掌握它们的常见操作和标准库函数,可以极大提高编码效率和代码可读性。
一、字符串(std::string)的常见操作和库函数 C++ 中的字符串使用 std::string 类,定义在 <string> 头文件中。
1. 构造与初始化 #include <string>
using namespace std ;
string s1 ; // 空字符串
string s2 = "hello" ; // 从C风格字符串构造
string s3 ( 5 , 'a' ); // "aaaaa"
string s4 ( s2 ); // 拷贝构造
string s5 ( s2 , 1 , 3 ); // 从s2的第1位置开始取3个字符 -> "ell"
2. 访问元素 char c1 = s2 [ 1 ]; // 'e',不检查越界
char c2 = s2 . at ( 1 ); // 'e',越界会抛出异常
int len = s2 . length (); // 或 s2.size(),返回字符串长度
bool isEmpty = s2 . empty (); // 是否为空
3. 遍历字符串 // 无下标,用于拼接比较多
for ( char c : s2 ) {
cout << c ;
}
// 或者下标遍历
for ( int i = 0 ; i < s2 . size (); ++ i ) {
cout << s2 [ i ];
}
4. 修改字符串 s2 . append ( " world" ); // s2变为"hello world"
// append可以追加字符串,不可以追加字符类型
// 追加字符可以使用push_back
s2 . push_back ( '!' ); // s2变为"hello world!"
// 也可以使用 += 追加字符或字符串
s2 += "!" ;
s2 . insert ( 5 , " " ); // 在第5位置插入空格 -> "hello world!"
s2 . insert ( s2 . end (), s3 . begin (), s3 . end ()); // 在s2末尾插入s3
s2 . erase ( 5 , 1 ); // 从第5位置删除1个字符
s2 . replace ( 0 , 5 , "hi" ); // 将[0,5)替换为"hi" -> "hi world!"
// 翻转字符串的某个区间
void reverseString ( string & s , int start , int end ) {
while ( start < end ) {
swap ( s [ start ++ ], s [ end -- ]);
}
}
// 使用库函数翻转
reverse ( s2 . begin (), s2 . begin () + 5 ); // 翻转字符串的前5个字符 "hello world!" -> "olleH world!"
5. 查找与替换 size_t pos = s2 . find ( "world" ); // 查找子串,返回起始索引,找不到返回 string::npos
if ( pos != string :: npos ) {
cout << "Found at: " << pos ;
}
pos = s2 . rfind ( "o" ); // 从后往前查找
s2 . replace ( pos , 1 , "a" ); // 替换找到的字符
// 判断前缀/后缀
bool starts = s2 . substr ( 0 , 2 ) == "he" ; // 手动判断前缀
bool startsWithHe = s2 . compare ( 0 , 2 , "he" ) == 0 ; // 更标准但麻烦
// C++20起有 starts_with() 和 ends_with()
C++20 新增:
s.starts_with("he")s.ends_with("ld!")6. 截取子串 string sub = s2 . substr ( 6 , 5 ); // 从第6位置开始,取5个字符 -> "world"
7. 转换大小写(需手动实现或使用算法) 标准库没有直接提供,但可以:
// 转小写/大写一般要自己写循环或者使用<cctype>
for ( char & c : s2 ) {
c = tolower ( c ); // 需要 #include <cctype>
}
// 使用transform
transform ( s2 . begin (), s2 . end (), s2 . begin (), :: toupper ); // 转大写
8. 字符串分割 / 拼接(通常需要自己实现或使用 stringstream) 拼接多个字符串可以用 + 或 append() 或 += 分割字符串一般用 stringstream + getline(..., delim) 示例(按空格分割):
string line = "a b c" ;
stringstream ss ( line );
string word ;
while ( ss >> word ) {
cout << word << endl ;
}
二、数组相关操作(原生数组 vs std::vector) 1. 原生数组(C-style array) 定义与初始化 int arr [ 5 ] = { 1 , 2 , 3 , 4 , 5 };
int arr2 [] = { 10 , 20 , 30 }; // 自动推导大小
常见操作 访问:arr[i] 长度:无法直接获取 ,除非额外保存 size 遍历:for 循环 排序等功能需要借助 <algorithm> 中的算法,传入首尾指针 翻转一个数组的某个区间:
void reverseArray ( int arr [], int start , int end ) {
while ( start < end ) {
swap ( arr [ start ++ ], arr [ end -- ]);
}
}
2. std::vector 动态数组 定义在 <vector> 头文件中。
构造与初始化 #include <vector>
using namespace std ;
vector < int > v1 ; // 空vector
vector < int > v2 ( 5 , 10 ); // 5个元素,都是10
vector < int > v3 = { 1 , 2 , 3 }; // 列表初始化
vector < int > v4 ( v3 ); // 拷贝构造
vector < int > v5 ( v3 . begin (), v3 . end ()); // 用迭代器范围构造
常用操作 获取信息 int size = v1 . size (); // 元素个数
bool isEmpty = v1 . empty (); // 是否为空
访问元素 int first = v3 [ 0 ]; // 不检查边界
int second = v3 . at ( 1 ); // 检查边界,越界抛异常
int last = v3 . back (); // 最后一个元素
int first2 = v3 . front (); // 第一个元素
修改容器 v1 . push_back ( 100 ); // 尾部插入
v1 . pop_back (); // 尾部删除
v1 . insert ( v1 . begin () + 1 , 99 ); // 在第1位置后插入99
v1 . erase ( v1 . begin ()); // 删除第一个元素
v1 . clear (); // 清空所有元素
遍历 // 下标遍历
for ( int i = 0 ; i < v1 . size (); ++ i ) {
cout << v1 [ i ];
}
// 迭代器遍历
for ( auto it = v1 . begin (); it != v1 . end (); ++ it ) {
cout << * it ;
}
// 范围for遍历(推荐)
for ( int x : v1 ) {
cout << x ;
}
排序 #include <algorithm>
sort ( v1 . begin (), v1 . end ()); // 升序排序
sort ( v1 . begin (), v1 . end (), greater < int > ()); // 降序排序
查找 auto it = find ( v1 . begin (), v1 . end (), 3 ); // 返回迭代器
if ( it != v1 . end ()) {
cout << "Found: " << * it ;
} else {
cout << "Not found" ;
}
去重(要先排序!) sort ( v1 . begin (), v1 . end ());
auto last = unique ( v1 . begin (), v1 . end ()); // 把重复的移到后面,返回新逻辑结尾
v1 . erase ( last , v1 . end ()); // 真正删除后面的重复元素
二维 vector vector < vector < int >> matrix ( 3 , vector < int > ( 4 , 0 )); // 3行4列,全0
三、常用算法库函数() 很多操作都可以用 <algorithm> 中的函数简化:
常用函数: 功能 函数 示例 排序 sort(begin, end)sort(v.begin(), v.end());逆序 reverse(begin, end)reverse(v.begin(), v.end());查找 find(begin, end, val)auto it = find(v.begin(), v.end(), 10);二分查找(必须有序) binary_search(begin, end, val)bool found = binary_search(v.begin(), v.end(), 10);二分查找边界 lower_bound, upper_bound用于查找第一个“不小于”或“大于”的位置 最大值/最小值 max(a, b), min(a, b),或 max_element, min_elementauto maxIt = max_element(v.begin(), v.end());交换 swap(a, b)swap(v[i], v[j]);填充 fill(begin, end, value)fill(v.begin(), v.end(), 0);拷贝 copy(src_begin, src_end, dest_begin)copy(src.begin(), src.end(), dest.begin());转换 transform可对每个元素做操作 填充指定次数 fill_n(dest_begin, count, value)
四、总结:字符串 & 数组常用操作速查 数据结构 常用操作 相关头文件 string 拼接(+)、查找(find)、截取(substr)、插入/删除、遍历、长度(.size()) <string>vector push_back/pop_back、insert/erase、sort/find、遍历、大小/容量 <vector>, <algorithm>原生数组 下标访问、配合算法库函数使用 <algorithm>, <cstring>(C风格字符串)通用算法 sort, find, reverse, min/max, transform 等 <algorithm>
推荐最佳实践:
优先使用 std::vector 而非原生数组 ,更安全、功能更强大。熟悉 <algorithm> 中的常用函数 ,比如 sort、find、reverse,能极大提升效率。字符串操作推荐用 std::string 的成员函数 ,比如 find、substr、append 等。注意边界条件 ,尤其在查找、删除、访问元素时。最长连续递增序列 最长连续递增序列
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:
输入:nums = [1,3,5,4,7]
输出:3
解释:最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
示例 2:
输入:nums = [2,2,2,2,2]
输出:1
解释:最长连续递增序列是 [2], 长度为1。
提示:
1 <= nums.length <= 104
-109 <= nums[i] <= 109
思路1 不断记录更新 作为模拟题,翻译出:
维护一个变量 max_len 记录当前最长连续递增子序列的长度。 遍历数组 nums,如果当前元素小于下一个元素,则 max_len 加一。 遇到减小的时候,就重置临时变量,待下一次连续递增子序列开始。 class Solution {
public:
int findLengthOfLCIS ( vector < int >& nums ) {
int n = nums . size ();
if ( n < 1 )
return n ;
int lenth = 1 ;
int maxLenth = 1 ;
for ( int i = 0 ; i < n - 1 ; i ++ ) {
if ( nums [ i + 1 ] > nums [ i ]) {
lenth ++ ;
maxLenth = max ( lenth , maxLenth );
} else {
lenth = 1 ;
}
}
return maxLenth ;
}
};
最长连续序列 最长连续序列
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
示例 2:
输入:nums = [0,3,7,2,5,8,4,6,0,1]
输出:9
示例 3:
输入:nums = [1,0,1,2]
输出:3
提示:
0 <= nums.length <= 105
-109 <= nums[i] <= 109
思路1 hashset查找 写法思路上和上一题一样,就是对照遍历的对象成了hashset。
先将所有元素加入到一个 hashset 中。 遍历数组中的每个元素,如果hashset中没有比当前元素数值小1的元素 ,说明当前元素是递增数列的开头节点 ,往后每次查加1的数值,直到加1寻找失败,断开区间,更新最大长度。 如果断开后找到的元素非头节点,重置长度为1 class Solution {
public:
int longestConsecutive ( vector < int >& nums ) {
int n = nums . size ();
if ( n < 1 ) {
return n ;
}
unordered_set < int > tempSet ;
for ( int val : nums ) {
tempSet . insert ( val );
}
int lenth = 1 ;
int maxLenth = 1 ;
for ( const int & num : tempSet ) {
// 当前元素是前驱元素
if ( ! tempSet . count ( num - 1 )) {
int curretnNum = num ;
while ( tempSet . count ( curretnNum + 1 )) {
lenth ++ ;
curretnNum += 1 ;
maxLenth = max ( maxLenth , lenth );
}
}
// 非前驱元素了,重置lenth
lenth = 1 ;
}
return maxLenth ;
}
};
思路2 排序后遍历 先排序原数组,再从头遍历,记录当前连续递增序列的长度,遇到断开了,就更新最大长度。
class Solution {
public:
int longestConsecutive ( vector < int >& nums ) {
// 处理边界情况:数组为空或只有一个元素
int max = 0 , length = 0 ;
if ( nums . size () <= 1 ) {
return nums . size () ? 1 : 0 ; // 空数组返回0,单元素返回1
}
// 先对数组进行排序,将可能连续的数字放在一起
std :: sort ( nums . begin (), nums . end ());
// 遍历排序后的数组,寻找连续序列
for ( int i = 0 ; i < nums . size () - 1 ; i ++ ) {
// 如果相邻元素差值为1,说明是连续序列
if ( nums [ i + 1 ] - nums [ i ] == 1 ) {
length ++ ; // 当前连续序列长度加1
}
// 如果相邻元素相等,跳过重复元素,继续检查下一个
if ( nums [ i + 1 ] == nums [ i ]) {
continue ;
}
// 如果相邻元素差值不为1,说明连续序列中断
if ( nums [ i + 1 ] - nums [ i ] != 1 ) {
// 更新最大长度(length是间隔数,序列长度需要+1)
if ( length + 1 > max ) {
max = length + 1 ;
}
length = 0 ; // 重置当前序列长度
}
}
// 检查最后一个连续序列(循环结束时可能还有未统计的序列)
if ( length + 1 > max ) {
max = length + 1 ;
}
// 返回最大长度,如果max为0说明没有连续序列,返回1(至少有一个元素)
return max ? max : 1 ;
}
};
有趣的注入现象 这个 atexit 函数覆盖了力扣系统写入的运行时间文件:
力扣先执行:写入真实运行时间 → display_runtime.txt 程序退出时你的代码执行:写入 “0” → display_runtime.txt(覆盖之前的内容) int init = atexit ([]()
{
//力扣是从main开始进行计算的,这里先调用过ofstream让他初始化好,后面就不需要初始化了,结果会更快
ofstream ( "display_runtime.txt" ) << "0" ;
});
合并两个有序数组 合并两个有序数组
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1
中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m
个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
解释:需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
解释:需要合并 [1] 和 [] 。
合并结果是 [1] 。
示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1
输出:[1]
解释:需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0
仅仅是为了确保合并结果可以顺利存放到 nums1 中。
提示:
nums1.length == m + n
nums2.length == n
0 <= m, n <= 200
1 <= m + n <= 200
-109 <= nums1[i], nums2[j] <= 109
进阶:你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗?
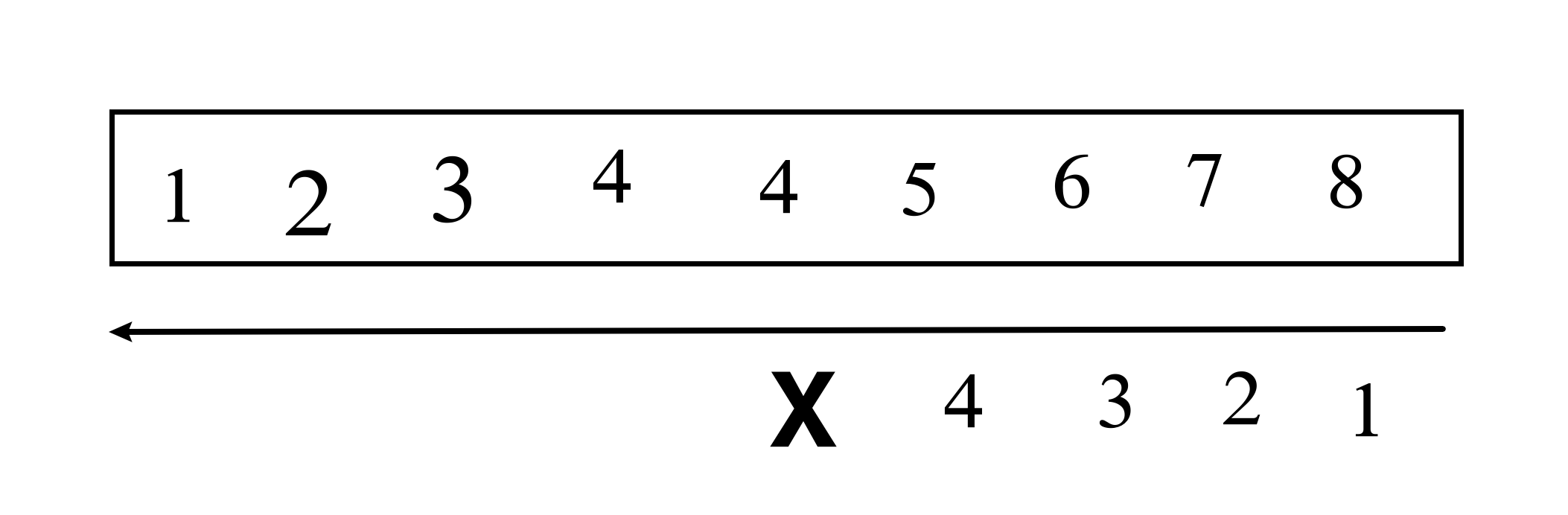
思路1 模拟题 从后往前遍历比较 从后往前只遍历一次,将两个数组的有效位一起拿来比较,如果一个数组的有效位使用完了,就设置为负的最小值来比较:
class Solution {
public:
void merge ( vector < int >& nums1 , int m , vector < int >& nums2 , int n ) {
int idxm = m - 1 ;
int idxn = n - 1 ;
for ( int i = m + n - 1 ; i >= 0 ; i -- ) {
int currentm = idxm >= 0 ? nums1 [ idxm ] : - INT_MAX ;
int currentn = idxn >= 0 ? nums2 [ idxn ] : - INT_MAX ;
currentm > currentn ? idxm -- : idxn -- ;
nums1 [ i ] = max ( currentm , currentn );
}
}
};
思路2 优化思路1中的极值写法 使用 -INT_MAX 来作为比较值不太优雅,优化判断条。
可以填充为nums1有效位的情况是, (nums1中元素没有走完) && (nums2中元素比nums1小 || nums2已经走完了)
剩下的情况就填充nums2的有效位。
class Solution {
public:
void merge ( vector < int >& nums1 , int m , vector < int >& nums2 , int n ) {
int idxm = m - 1 ;
int idxn = n - 1 ;
for ( int i = m + n - 1 ; i >= 0 ; i -- ) {
if ( idxm >= 0 && ( idxn < 0 || nums1 [ idxm ] > nums2 [ idxn ])) {
nums1 [ i ] = nums1 [ idxm -- ];
} else {
nums1 [ i ] = nums2 [ idxn -- ];
}
}
}
};
思路3 从后往前填充 判断条件不同 因为nums1空间足够,可以直接两个数组一起对比遍历,从后往前遍历,每次取两个数组中较大的一个,放到nums1的最后面。
class Solution {
public:
void merge ( vector < int >& nums1 , int m , vector < int >& nums2 , int n ) {
int i = m - 1 , j = n - 1 , k = m + n - 1 ;
while ( i >= 0 && j >= 0 ) {
if ( nums1 [ i ] > nums2 [ j ]) {
nums1 [ k -- ] = nums1 [ i -- ];
} else {
nums1 [ k -- ] = nums2 [ j -- ];
}
}
// 如果nums2还有剩余元素
while ( j >= 0 ) {
nums1 [ k -- ] = nums2 [ j -- ];
}
}
};
如果第一个数组有效位比第二个数组多,那么第一个循环走完,整个nums1其实已经是自动排完序的了;
如果第二个数组元素比第一个数组有效位多,那么第一个循环走完,第二个数组还有剩余的元素,而且这些剩余元素都是最小的,第二遍循环将这些元素直接放到nums1的前面即可。
思路4 使用sort库函数 将第二个数组添加到第一个数组尾部,直接调用sort方法。
class Solution {
public:
void merge ( vector < int >& nums1 , int m , vector < int >& nums2 , int n ) {
for ( int i = 0 ; i != n ; ++ i ) {
nums1 [ m + i ] = nums2 [ i ];
}
sort ( nums1 . begin (), nums1 . end ());
}
};
移除元素 移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。
假设 nums 中不等于 val 的元素数量为 k,要通过此题,您需要执行以下操作:
更改 nums 数组,使 nums 的前 k 个元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。
返回 k。
用户评测:
评测机将使用以下代码测试您的解决方案:
int[] nums = [...]; // 输入数组
int val = ...; // 要移除的值
int[] expectedNums = [...]; // 长度正确的预期答案。
// 它以不等于 val 的值排序。
int k = removeElement(nums, val); // 调用你的实现
assert k == expectedNums.length;
sort(nums, 0, k); // 排序 nums 的前 k 个元素
for (int i = 0; i < actualLength; i++) {
assert nums[i] == expectedNums[i];
}
如果所有的断言都通过,你的解决方案将会 通过。
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2,_,_]
解释:你的函数函数应该返回 k = 2, 并且 nums 中的前两个元素均为 2。
你在返回的 k 个元素之外留下了什么并不重要(因此它们并不计入评测)。
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3,_,_,_]
解释:你的函数应该返回 k = 5,并且 nums 中的前五个元素为 0,0,1,3,4。
注意这五个元素可以任意顺序返回。
你在返回的 k 个元素之外留下了什么并不重要(因此它们并不计入评测)。
提示:
0 <= nums.length <= 100
0 <= nums[i] <= 50
0 <= val <= 100
思路1 双指针 快慢指针,题目要求原地移除所有等于val的元素。快指针往前遍历,慢指针代表留存元素的位置。快指针的值不等于要移除元素时,说明这个值需要留存,将快指针的值复制到慢指针指向的位置,快慢指针同时往前;当快指针指向了要移除的元素时,此时慢指针一定也指向了要移除的元素,慢指针不动,此位置要接受下一个留存的值,只移动快指针。
class Solution {
public:
int removeElement ( vector < int >& nums , int val ) {
int n = nums . size ();
int left = 0 ;
for ( int right = 0 ; right < n ; right ++ ) {
if ( nums [ right ] != val ) {
nums [ left ] = nums [ right ];
left ++ ;
}
}
return left ;
}
};
删除有序数组中的重复项 删除有序数组中的重复项
给你一个 非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题解可以被通过:
更改数组 nums ,使 nums 的前 k 个元素包含唯一元素,并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
返回 k 。
判题标准:
系统会用下面的代码来测试你的题解:
int[] nums = [...]; // 输入数组
int[] expectedNums = [...]; // 长度正确的期望答案
int k = removeDuplicates(nums); // 调用
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums[i] == expectedNums[i];
}
如果所有断言都通过,那么您的题解将被 通过。
示例 1:
输入:nums = [1,1,2]
输出:2, nums = [1,2,_]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
提示:
1 <= nums.length <= 3 * 104
-104 <= nums[i] <= 104
nums 已按 非严格递增 排列
思路1 双指针 和上一题类似,快慢指针,快指针遍历数组,慢指针代表不重复元素的位置。快指针遍历到的元素如果和慢指针指向的元素不同,说明这个元素是不重复的,将快指针指向的元素复制到慢指针指向的位置,快慢指针同时往前;如果快指针指向的元素和慢指针指向的元素相同,说明这个元素是重复的,只移动快指针。慢指针停留在此处等待写入新的不重复元素。
class Solution {
public:
int removeDuplicates ( vector < int >& nums ) {
int n = nums . size ();
int left = 0 ;
for ( int right = 0 ; right < n ; right ++ ) {
if ( nums [ right ] != nums [ left ]) {
left ++ ;
nums [ left ] = nums [ right ];
}
}
// left 是下标,加1为长度
return left + 1 ;
}
};
删除有序数组中的重复项 II 删除有序数组中的重复项 II
给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参做任何拷贝
int len = removeDuplicates(nums);
// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
print(nums[i]);
}
示例 1:
输入:nums = [1,1,1,2,2,3]
输出:5, nums = [1,1,2,2,3]
解释:函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3。 不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,1,2,3,3]
输出:7, nums = [0,0,1,1,2,3,3]
解释:函数应返回新长度 length = 7, 并且原数组的前七个元素被修改为 0, 0, 1, 1, 2, 3, 3。不需要考虑数组中超出新长度后面的元素。
提示:
1 <= nums.length <= 3 * 104
-104 <= nums[i] <= 104
nums 已按升序排列
思路1 双指针 处理后的数组最短长度一定比2大,因为每个元素最多出现两次。所以短数组特殊处理,快慢指针起点直接从下标2开始。较上一题基础题,唯一的不同就是处理好留存元素和位置的判断条件。
这里因为是有序数组,所以从慢指针的前两个元素进行判断,表示当前元素是否和前两个元素重复。如果重复,说明当前元素需要被删除,只移动快指针;如果不重复,说明当前元素需要被保留,将快指针指向的元素复制到慢指针指向的位置,快慢指针同时往前。
class Solution {
public:
int removeDuplicates ( vector < int >& nums ) {
int n = nums . size ();
if ( n <= 2 ) {
return n ;
}
int slow = 2 , fast = 2 ;
while ( fast < n ) {
if ( nums [ slow - 2 ] != nums [ fast ]) {
nums [ slow ] = nums [ fast ];
++ slow ;
}
++ fast ;
}
return slow ;
}
};
多数元素 多数元素
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:nums = [3,2,3]
输出:3
示例 2:
输入:nums = [2,2,1,1,1,2,2]
输出:2
提示:
n == nums.length
1 <= n <= 5 * 104
-109 <= nums[i] <= 109
思路1 哈希表 用哈希表记录每个元素出现的次数,遍历哈希表,找到出现次数大于n/2的元素。
class Solution {
public:
int majorityElement ( vector < int >& nums ) {
int n = nums . size ();
unordered_map < int , int > map ;
for ( int i = 0 ; i < n ; i ++ ) {
map [ nums [ i ]] ++ ;
}
for ( auto it = map . begin (); it != map . end (); it ++ ) {
if ( it -> second > n / 2 ) {
return it -> first ;
}
}
return - 1 ;
}
};
找到出现次数最多的元素 如果不一定有出现次数大于 n/2 的元素,而是需要是找出现次数最多的元素 。相较于思路1,只需要遍历哈希表时,不断交换最大值,找到出现次数最多的元素即可。
class Solution {
public:
int majorityElement ( vector < int >& nums ) {
int n = nums . size ();
unordered_map < int , int > map ;
for ( int i = 0 ; i < n ; i ++ ) {
map [ nums [ i ]] ++ ;
}
int max = 0 ;
int maxItem = nums [ 0 ];
for ( auto it = map . cbegin (); it != map . cend (); it ++ ) {
if ( it -> second > max ) {
maxItem = it -> first ;
max = it -> second ;
}
}
return maxItem ;
}
};
排序后直接取中点的元素 如果将数组 nums 中的所有元素按照单调递增或单调递减的顺序排序,那么下标为 n/2 的元素(下标从 0 开始)一定是众数。
class Solution {
public:
int majorityElement ( vector < int >& nums ) {
int n = nums . size ();
sort ( nums . begin (), nums . end ());
return nums [ n / 2 ];
}
};
轮转数组 轮转数组
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
提示:
1 <= nums.length <= 105
-231 <= nums[i] <= 231 - 1
0 <= k <= 105
思路1 使用额外的数组直接承接 因为k有可能是大于n的,即有可能轮换一整轮还要多。所以原数组中,每个的元素位置为 k + i % n 取余。
class Solution {
public:
void rotate ( vector < int >& nums , int k ) {
int n = nums . size ();
vector < int > temp ( n );
for ( int i = 0 ; i < n ; i ++ ) {
temp [( k + i ) % n ] = nums [ i ];
}
nums = temp ;
}
};
思路2 上一个方案的变体 直接拼接nums两遍,找到轮转后的起始位置,从这里取值,取n次填到原数组中去。
class Solution {
public:
void rotate ( vector < int >& nums , int k ) {
int n = nums . size (); // 获取数组的长度
// 创建一个临时数组 temp,并将原数组 nums 的内容拷贝进去
vector < int > temp = nums ;
// 关键步骤:将原数组 nums 再次拼接到 temp 后面
// 这样就可以通过选取合适的起始位置,来得到旋转后的数组
temp . insert ( temp . end (), nums . begin (), nums . end ());
// 计算旋转的起始位置:
// 我们想把原数组向右旋转 k 个位置。
// 为了便于计算,我们令 start = n - k % n
// 注意:k 可能大于 n,所以要取模:k % n
int start = n - k % n ;
// 这 n 个连续元素,就是原数组旋转 k 次后的正确顺序
for ( int i = 0 ; i < n ; i ++ ) {
nums [ i ] = temp [ start + i ];
}
}
};
思路3 三次反转 流程如下表:
操作 结果 原始数组 1 2 3 4 5 6 7 翻转所有元素 7 6 5 4 3 2 1 翻转 [0,kmodn−1] 区间的元素 5 6 7 4 3 2 1 翻转 [kmodn,n−1] 区间的元素 5 6 7 1 2 3 4
class Solution {
public:
void reverse ( vector < int >& nums , int left , int right ) {
while ( left < right ) {
swap ( nums [ left ], nums [ right ]);
left ++ ;
right -- ;
}
}
void rotate ( vector < int >& nums , int k ) {
int n = nums . size ();
k %= n ;
reverse ( nums . begin (), nums . end ());
reverse ( nums . begin (), nums . begin () + k );
reverse ( nums . begin () + k , nums . end ());
}
};
字符串轮转 要求同上,将数组改为字符串:
class Solution {
public:
void rotate ( string & str , int k ) {
int n = str . size ();
string temp = str + str ;
int start = n - k % n ;
str = temp . substr ( start , n );
}
};
字符串的方法比数组简单,直接使用加号拼接,使用 substr 来取范围。
买卖股票的最佳时机 买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 105
0 <= prices[i] <= 104
思路1 一次遍历 从左往右,碰到最小的就更新 min 值,代表买入时机。碰到差值最大的就更新 maxProfit 值,代表所能赚取的最大利润。
class Solution {
public:
int maxProfit ( vector < int >& prices ) {
int min = 10000 ;
int maxProfit = 0 ;
int n = prices . size ();
for ( int i = 0 ; i < n ; i ++ ) {
if ( prices [ i ] < min ) {
min = prices [ i ];
} else if ( prices [ i ] - min > maxProfit ) {
maxProfit = prices [ i ] - min ;
}
}
return maxProfit ;
}
};
买卖股票的最佳时机 II 买卖股票的最佳时机 II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。然而,你可以在 同一天 多次买卖该股票,但要确保你持有的股票不超过一股。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3。
最大总利润为 4 + 3 = 7 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
最大总利润为 4 。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0。
提示:
1 <= prices.length <= 3 * 104
0 <= prices[i] <= 104
思路1 一次遍历 从左往右,碰到比前一天价格高的,就计算利润并加入到总利润中。即拥有所有收益,避开所有亏损, 这个计算方式和最优的买入卖出操作效果等价 。
class Solution {
public:
int maxProfit ( vector < int >& prices ) {
int maxProfit = 0 ;
int n = prices . size ();
for ( int i = 1 ; i < n ; i ++ ) {
if ( prices [ i ] > prices [ i - 1 ]) {
maxProfit += prices [ i ] - prices [ i - 1 ];
}
}
return maxProfit ;
}
};
跳跃游戏 跳跃游戏
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
提示:
1 <= nums.length <= 104
0 <= nums[i] <= 105
思路1 贪心 根据题目的描述,只要存在一个位置 x,它本身可以到达,并且它跳跃的最大长度为 x+nums[x],这个值大于等于 y,即 x+nums[x]≥y,那么位置 y 也可以到达。
满足可达的条件之后,不断更新 x+nums[x] 这个最远可达的位置,最终这个值越过或者可以到达最后一个下标即为成功,否则失败。
class Solution {
public:
bool canJump ( vector < int >& nums ) {
int n = nums . size ();
int rightmost = 0 ;
for ( int i = 0 ; i < n ; ++ i ) {
// 判断当前位置 i 是否可达
if ( i <= rightmost ) {
// 更新最远可达位置
rightmost = max ( rightmost , i + nums [ i ]);
// 如果最远可达位置大于等于最后一个下标,返回 true
if ( rightmost >= n - 1 ) {
return true ;
}
}
}
// 如果遍历完成,最远可达位置还不到最后一个下标,返回 false
return false ;
}
};
跳跃游戏 II 跳跃游戏 II
给定一个长度为 n 的 0 索引整数数组 nums。初始位置在下标 0。
每个元素 nums[i] 表示从索引 i 向后跳转的最大长度。换句话说,如果你在索引 i 处,你可以跳转到任意 (i + j) 处:
0 <= j <= nums[i] 且 i + j < n
返回到达 n - 1 的最小跳跃次数。测试用例保证可以到达 n - 1。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
提示:
1 <= nums.length <= 104
0 <= nums[i] <= 1000
题目保证可以到达 n - 1
思路1 贪心 正向查找 每次到达某个位置时,计算可达位置之后可以跳跃的最远距离,记录下这个最远距离,当到达这个最远距离时,跳跃次数加一。 不管内部选取哪一个点作为下一个起跳点,经过这个最远边界时,一定只需要增加跳跃一次 。
在遍历数组时,我们不访问最后一个元素,这是因为在访问最后一个元素之前,我们的边界一定大于等于最后一个位置,否则就无法跳到最后一个位置了。如果访问最后一个元素,在边界正好为最后一个位置的情况下,我们会增加一次「不必要的跳跃次数」,因此我们不必访问最后一个元素。
class Solution {
public:
int jump ( vector < int >& nums ) {
int maxPos = 0 , n = nums . size (), end = 0 , step = 0 ;
for ( int i = 0 ; i < n - 1 ; i ++ ) {
if ( i <= maxPos ) {
maxPos = max ( maxPos , i + nums [ i ]);
if ( end == i ) {
end = maxPos ;
step ++ ;
}
}
}
return step ;
}
};
H指数 H指数
给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。
根据维基百科上 h 指数的定义:h 代表“高引用次数” ,一名科研人员的 h 指数 是指他(她)至少发表了 h 篇论文,并且 至少 有 h 篇论文被引用次数大于等于 h 。如果 h 有多种可能的值,h 指数 是其中最大的那个。
示例 1:
输入:citations = [3,0,6,1,5]
输出:3
解释:给定数组表示研究者总共有 5 篇论文,每篇论文相应的被引用了 3, 0, 6, 1, 5 次。
由于研究者有 3 篇论文每篇 至少 被引用了 3 次,其余两篇论文每篇被引用 不多于 3 次,所以她的 h 指数是 3。
示例 2:
输入:citations = [1,3,1]
输出:1
提示:
n == citations.length
1 <= n <= 5000
0 <= citations[i] <= 1000
思路1 两遍遍历 按照题目描述的计算规则写逻辑即可,O(n^2) 的时间复杂度。
class Solution {
public:
int hIndex ( vector < int >& citations ) {
int n = citations . size (), hIndex = 0 ;
for ( int i = 0 ; i < n ; i ++ ) {
int count = 0 ;
for ( int j = 0 ; j < n ; j ++ ) {
if ( citations [ i ] <= citations [ j ] && citations [ i ] > count ) {
count ++ ;
}
}
hIndex = max ( hIndex , count );
}
return hIndex ;
}
};
排序后逆序遍历 根据 H 指数的定义,如果当前 H 指数为 h 并且在遍历过程中找到当前值 citations[i]>h,则说明我们找到了一篇被引用了至少 h+1 次的论文,所以将现有的 h 值加 1。继续遍历直到 h 无法继续增大。最后返回 h 作为最终答案。
class Solution {
public:
int hIndex ( vector < int >& citations ) {
int hIndex = 0 , i = citations . size () - 1 ;
sort ( citations . begin (), citations . end ());
while ( i >= 0 && citations [ i ] > hIndex ) {
hIndex ++ ;
i -- ;
}
return hIndex ;
}
};
O(1) 时间插入、删除和获取随机元素 O(1) 时间插入、删除和获取随机元素
实现RandomizedSet 类:
RandomizedSet() 初始化 RandomizedSet 对象
bool insert(int val) 当元素 val 不存在时,向集合中插入该项,并返回 true ;否则,返回 false 。
bool remove(int val) 当元素 val 存在时,从集合中移除该项,并返回 true ;否则,返回 false 。
int getRandom() 随机返回现有集合中的一项(测试用例保证调用此方法时集合中至少存在一个元素)。每个元素应该有 相同的概率 被返回。
你必须实现类的所有函数,并满足每个函数的 平均 时间复杂度为 O(1) 。
示例:
输入
["RandomizedSet", "insert", "remove", "insert", "getRandom", "remove", "insert", "getRandom"]
[[], [1], [2], [2], [], [1], [2], []]
输出
[null, true, false, true, 2, true, false, 2]
解释
RandomizedSet randomizedSet = new RandomizedSet();
randomizedSet.insert(1); // 向集合中插入 1 。返回 true 表示 1 被成功地插入。
randomizedSet.remove(2); // 返回 false ,表示集合中不存在 2 。
randomizedSet.insert(2); // 向集合中插入 2 。返回 true 。集合现在包含 [1,2] 。
randomizedSet.getRandom(); // getRandom 应随机返回 1 或 2 。
randomizedSet.remove(1); // 从集合中移除 1 ,返回 true 。集合现在包含 [2] 。
randomizedSet.insert(2); // 2 已在集合中,所以返回 false 。
randomizedSet.getRandom(); // 由于 2 是集合中唯一的数字,getRandom 总是返回 2 。
提示:
-231 <= val <= 231 - 1
最多调用 insert、remove 和 getRandom 函数 2 * 105 次
在调用 getRandom 方法时,数据结构中 至少存在一个 元素。
思路1 哈希表 + 数组 要求实现 O(1) 时间的插入、删除和获取随机元素操作。已知哈希表的搜索元素复杂度是 O(1) ,即插入删除很快,但是无下标,无法完成随机获取元素。而动态数组可以根据下标随机获取元素,但是插入和删除,搜索元素的复杂度是O(n),可以将二者结合起来,数组用来实际的存储元素,哈希表来记录下标和元素值。
class RandomizedSet {
public:
RandomizedSet () {
srand (( unsigned ) time ( NULL ));
}
bool insert ( int val ) {
if ( indices . count ( val )) {
return false ;
}
int index = nums . size ();
nums . emplace_back ( val );
indices [ val ] = index ;
return true ;
}
bool remove ( int val ) {
if ( ! indices . count ( val )) {
return false ;
}
int index = indices [ val ];
int last = nums . back ();
nums [ index ] = last ;
indices [ last ] = index ;
nums . pop_back ();
indices . erase ( val );
return true ;
}
int getRandom () {
// 测试用例保证调用此方法时集合中至少存在一个元素
int randomIndex = rand () % nums . size ();
return nums [ randomIndex ];
}
private:
vector < int > nums ;
unordered_map < int , int > indices ;
};
srand((unsigned)time(NULL)); 根据程序运行时间,生成随机数种子。rand() 函数根据这个种子生成随机数。如果不设置种子,rand() 函数会根据一个默认的种子生成随机数,这会导致每次运行程序时生成的随机数序列相同。
插入操作时,首先判断 val 是否在哈希表中,如果已经存在则返回 false,如果不存在则插入 val,操作如下:如果 val 不在哈希表中,将 val 插入变长数组的末尾; 在添加 val 之前的变长数组长度为 val 所在下标 index,将 val 和下标 index 存入哈希表; 返回 true。 删除操作时,首先判断 val 是否在哈希表中,如果不存在则返回 false,如果存在则删除 val,操作如下:从哈希表中获得 val 的下标 index; 将变长数组的最后一个元素 last 移动到下标 index 处,在哈希表中将 last 的下标更新为 index; 在变长数组中删除最后一个元素,在哈希表中删除 val; 返回 true。 删除操作的重点在于将变长数组的最后一个元素移动到待删除元素的下标处,然后删除变长数组的最后一个元素。该操作的时间复杂度是 O(1),且可以保证在删除操作之后变长数组中的所有元素的下标都连续,方便插入操作和获取随机元素操作。
获取随机元素操作时,由于变长数组中的所有元素的下标都连续,因此随机选取一个下标,返回变长数组中该下标处的元素。 除自身以外数组的乘积 除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法,且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
提示:
2 <= nums.length <= 105
-30 <= nums[i] <= 30
输入 保证 数组 answer[i] 在 32 位 整数范围内
进阶:你可以在 O(1) 的额外空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组 不被视为 额外空间。)
思路1 左右乘积列表 我们不必将所有数字的乘积除以给定索引处的数字得到相应的答案,而是利用索引左侧所有数字的乘积和右侧所有数字的乘积(即前缀与后缀)相乘得到答案。
对于给定索引 i,我们将使用它左边所有数字的乘积乘以右边所有数字的乘积。下面让我们更加具体的描述这个算法。
算法步骤:
初始化两个空数组 L 和 R。对于给定索引 i,L[i] 代表的是 i 左侧所有数字的乘积,R[i] 代表的是 i 右侧所有数字的乘积。 我们需要用两个循环来填充 L 和 R 数组的值。
对于数组 L,L[0] 应该是 1,因为第一个元素的左边没有元素。对于其他元素:L[i] = L[i-1] * nums[i-1]。 同理,对于数组 R,R[length-1] 应为 1。length 指的是输入数组的大小。其他元素:R[i] = R[i+1] * nums[i+1]。 当 R 和 L 数组填充完成,我们只需要在输入数组上迭代,且索引 i 处的值为:L[i] * R[i]。
class Solution {
public:
vector < int > productExceptSelf ( vector < int >& nums ) {
int n = nums . size ();
vector < int > multiNums ( n );
vector < int > left ( n , 0 );
vector < int > right ( n , 0 );
left [ 0 ] = 1 ;
for ( int i = 1 ; i < n ; i ++ ) {
// 此元素左侧所有乘积,为上一个left的总乘积,再乘以它左边的这个元素
left [ i ] = left [ i - 1 ] * nums [ i - 1 ];
}
right [ n - 1 ] = 1 ;
for ( int j = n - 2 ; j >= 0 ; j -- ) {
// 元素右边乘积,为之前的总乘积数值,再乘以其右边元素
right [ j ] = right [ j + 1 ] * nums [ j + 1 ];
}
for ( int i = 0 ; i < n ; i ++ ) {
multiNums [ i ] = left [ i ] * right [ i ];
}
return multiNums ;
}
};
加油站 加油站
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
因此,3 可为起始索引。
示例 2:
输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。
因此,无论怎样,你都不可能绕环路行驶一周。
提示:
n == gas.length == cost.length
1 <= n <= 105
0 <= gas[i], cost[i] <= 104
输入保证答案唯一。
思路1 嵌套循环(时间超限制) 构建了两个临时列表,gasExt和costExt,分别是gas和cost的扩展列表,长度为2n。方便从不同索引位置开始走一轮。
每到一个站点,都计算一次剩余油量,小于0就说明从这个站点出发不能走完全程,尝试下一个站点。如果剩余油量大于等于0,说明走完一轮了。
class Solution {
public:
int canCompleteCircuit ( vector < int >& gas , vector < int >& cost ) {
int n = gas . size ();
vector < int > gasExt = {};
gasExt . insert ( gasExt . end (), gas . begin (), gas . end ());
gasExt . insert ( gasExt . end (), gas . begin (), gas . end ());
vector < int > costExt = {};
costExt . insert ( costExt . end (), cost . begin (), cost . end ());
costExt . insert ( costExt . end (), cost . begin (), cost . end ());
for ( int i = 0 ; i < n ; i ++ ) {
int gasRemain = 0 ;
// 尝试从位置0出发,计算本轮的耗油量
for ( int j = i ; j < n + i ; j ++ ) {
gasRemain = gasRemain + gasExt [ j ] - costExt [ j ];
// 中途不够了,开始下一轮
if ( gasRemain < 0 ) {
break ;
}
}
if ( gasRemain < 0 ) {
continue ;
}
// 油量足够,返回这个索引
if ( gasRemain >= 0 ) {
return i ;
}
}
return - 1 ;
}
};
官方 贪心算法 待理解疏通:
class Solution {
public:
int canCompleteCircuit ( vector < int >& gas , vector < int >& cost ) {
int n = gas . size ();
int i = 0 ;
while ( i < n ) {
int sumOfGas = 0 , sumOfCost = 0 ;
int cnt = 0 ;
while ( cnt < n ) {
int j = ( i + cnt ) % n ;
sumOfGas += gas [ j ];
sumOfCost += cost [ j ];
if ( sumOfCost > sumOfGas ) {
break ;
}
cnt ++ ;
}
if ( cnt == n ) {
return i ;
} else {
i = i + cnt + 1 ;
}
}
return - 1 ;
}
};
分发糖果 分发糖果
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
你需要按照以下要求,给这些孩子分发糖果:
每个孩子至少分配到 1 个糖果。
相邻两个孩子中,评分更高的那个会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
示例 1:
输入:ratings = [1,0,2]
输出:5
解释:你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。
示例 2:
输入:ratings = [1,2,2]
输出:4
解释:你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果,这满足题面中的两个条件。
提示:
n == ratings.length
1 <= n <= 2 * 104
0 <= ratings[i] <= 2 * 104
左右各遍历一次取最大值 为了满足上述两个条件,一个常用且高效的解法是: 分别 从左到右 和 从右到左 遍历两次,确保两边相邻的约束都满足,然后取两边较大的那个值作为每个孩子最终的糖果数。
class Solution {
public:
int candy ( vector < int >& ratings ) {
int n = ratings . size (); // 获取孩子数量
// 初始化一个数组left,用于存储每个孩子从左到右比较时应该得到的糖果数
vector < int > left ( n );
// 第一个孩子至少给1颗糖果
left [ 0 ] = 1 ;
// 从左到右遍历,处理递增序列
for ( int i = 1 ; i < n ; i ++ ) {
if ( ratings [ i ] > ratings [ i - 1 ]) {
// 如果当前孩子评分比左边高,则糖果数比左边多1
left [ i ] = left [ i - 1 ] + 1 ;
} else {
// 否则,当前孩子至少给1颗糖果
left [ i ] = 1 ;
}
}
// right变量记录从右到左遍历时当前孩子应得的糖果数
int right = 1 ;
// 初始总数为最后一个孩子的较大值(left和right的初始值)
// 做从右往左遍历过程中,把左侧的结果考虑进去,一起算出总结果
int count = max ( right , left [ n - 1 ]);
// 从右到左遍历,处理递减序列
for ( int i = n - 2 ; i >= 0 ; i -- ) {
if ( ratings [ i ] > ratings [ i + 1 ]) {
// 如果当前孩子评分比右边高,则糖果数比右边多1
right = right + 1 ;
} else {
// 否则,当前孩子至少给1颗糖果
right = 1 ;
}
// 对于每个孩子,取左右两个方向计算值的较大者,保证同时满足两个条件
count += max ( right , left [ i ]);
}
return count ; // 返回总糖果数
}
};
接雨水 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105
实例1配图:
思路1 动态规划 对于下标 i,下雨后水能到达的最大高度等于下标 i 两边的最大高度的最小值,下标 i 处能接的雨水量等于下标 i 处的水能到达的最大高度减去 height[i]。
不能遍历到每一个下标处都遍历一次左右元素找最高值,这样时间复杂度就是O(n^2)了。可以利用 除自身以外数组的乘积 这题的思想,遍历多次,动态维护两个列表。
创建两个长度为 n 的数组 leftMax 和 rightMax 。对于 0≤i<n ,leftMax[i] 表示下标 i 及其左边的位置中,height 的最大高度,rightMax[i] 表示下标 i 及其右边的位置中,height 的最大高度。
显然,leftMax[0]=height[0],rightMax[n−1]=height[n−1] 。两个数组的其余元素的计算如下:
当 1≤i≤n−1 时,leftMax[i]=max(leftMax[i−1],height[i]);
当 0≤i≤n−2 时,rightMax[i]=max(rightMax[i+1],height[i])。
因此可以正向遍历数组 height 得到数组 leftMax 的每个元素值,反向遍历数组 height 得到数组 rightMax 的每个元素值。
在得到数组 leftMax 和 rightMax 的每个元素值之后,对于 0≤i<n ,下标 i 处能接的雨水量等于 min(leftMax[i],rightMax[i])−height[i]。遍历每个下标位置即可得到能接的雨水总量。
class Solution {
public:
int trap ( vector < int >& height ) {
int n = height . size ();
int count = 0 ;
vector < int > leftMax ( n );
vector < int > rightMax ( n );
// 初始化leftMax数组,从左到右遍历,记录每个位置左边的最大高度
int leftMaxTemp = height [ 0 ];
for ( int i = 0 ; i < n ; i ++ ) {
leftMaxTemp = max ( leftMaxTemp , height [ i ]);
leftMax [ i ] = leftMaxTemp ;
}
// 初始化rightMax数组,从右到左遍历,记录每个位置右边的最大高度
int rightMaxTemp = height [ n - 1 ];
for ( int i = n - 1 ; i >= 0 ; i -- ) {
rightMaxTemp = max ( rightMaxTemp , height [ i ]);
rightMax [ i ] = rightMaxTemp ;
}
// 计算每个位置的接水量,累加得到总接水量
for ( int i = 0 ; i < n ; i ++ ) {
int currentRain = min ( rightMax [ i ], leftMax [ i ]) - height [ i ];
if ( currentRain < 0 ) {
currentRain = 0 ;
}
count += currentRain ;
}
return count ;
}
};
小结 对于这种需要看 元素自身和其他所有元素的相对关系 的算法题,可以参考这两题的解法,还有分发糖果题目也是如此,左右各遍历一遍,取最大或者最小值,作为最终的正确结果。
罗马数字转整数 罗马数字转整数
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1 。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I 可以放在 V (5) 和 X (10) 的左边,来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边,来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边,来表示 400 和 900。
给定一个罗马数字,将其转换成整数。
示例 1:
输入: s = "III"
输出: 3
示例 2:
输入: s = "IV"
输出: 4
示例 3:
输入: s = "IX"
输出: 9
示例 4:
输入: s = "LVIII"
输出: 58
解释: L = 50, V= 5, III = 3.
示例 5:
输入: s = "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.
提示:
1 <= s.length <= 15
s 仅含字符 ('I', 'V', 'X', 'L', 'C', 'D', 'M')
题目数据保证 s 是一个有效的罗马数字,且表示整数在范围 [1, 3999] 内
题目所给测试用例皆符合罗马数字书写规则,不会出现跨位等情况。
IL 和 IM 这样的例子并不符合题目要求,49 应该写作 XLIX,999 应该写作 CMXCIX 。
关于罗马数字的详尽书写规则,可以参考 罗马数字 - 百度百科。
思路1 模拟 通常情况下,罗马数字中小的数字在大的数字的右边。若输入的字符串满足该情况,那么可以将每个字符视作一个单独的值,累加每个字符对应的数值即可。
例如 XXVII 可视作 X+X+V+I+I=10+10+5+1+1=27。
即一般都是大数在左边,小数在右边,所以可以直接累加每个字符对应的数值,若一个数字右侧的数字比它大,则将该数字的符号取反。
例如 XIV 可视作 X−I+V=10−1+5=14。
class Solution {
private:
unordered_map < char , int > numMap = {
{ 'I' , 1 }, { 'V' , 5 }, { 'X' , 10 }, { 'L' , 50 },
{ 'C' , 100 }, { 'D' , 500 }, { 'M' , 1000 },
};
public:
int romanToInt ( string s ) {
int n = s . size ();
int num = 0 ;
int count = 0 ;
for ( int i = 0 ; i < n - 1 ; i ++ ) {
if ( numMap [ s [ i ]] < numMap [ s [ i + 1 ]]) {
count -= numMap [ s [ i ]];
} else {
count += numMap [ s [ i ]];
}
}
count += numMap [ s [ n - 1 ]];
return count ;
}
};
整数转罗马数字 整数转罗马数字
七个不同的符号代表罗马数字,其值如下:
符号 值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
罗马数字是通过添加从最高到最低的小数位值的转换而形成的。将小数位值转换为罗马数字有以下规则:
如果该值不是以 4 或 9 开头,请选择可以从输入中减去的最大值的符号,将该符号附加到结果,减去其值,然后将其余部分转换为罗马数字。
如果该值以 4 或 9 开头,使用 减法形式,表示从以下符号中减去一个符号,例如 4 是 5 (V) 减 1 (I): IV ,9 是 10 (X) 减 1 (I):IX。仅使用以下减法形式:4 (IV),9 (IX),40 (XL),90 (XC),400 (CD) 和 900 (CM)。
只有 10 的次方(I, X, C, M)最多可以连续附加 3 次以代表 10 的倍数。你不能多次附加 5 (V),50 (L) 或 500 (D)。如果需要将符号附加4次,请使用 减法形式。
给定一个整数,将其转换为罗马数字。
示例 1:
输入:num = 3749
输出: "MMMDCCXLIX"
解释:
3000 = MMM 由于 1000 (M) + 1000 (M) + 1000 (M)
700 = DCC 由于 500 (D) + 100 (C) + 100 (C)
40 = XL 由于 50 (L) 减 10 (X)
9 = IX 由于 10 (X) 减 1 (I)
注意:49 不是 50 (L) 减 1 (I) 因为转换是基于小数位
示例 2:
输入:num = 58
输出:"LVIII"
解释:
50 = L
8 = VIII
示例 3:
输入:num = 1994
输出:"MCMXCIV"
解释:
1000 = M
900 = CM
90 = XC
4 = IV
提示:
1 <= num <= 3999
思路1 遍历搜索法 维护四个map,对应从个位到千位上0-9的罗马数字。解析出每个位上的数字,根据罗马数字的规则,将其转换为罗马数字。
const string thousands [] = { "" , "M" , "MM" , "MMM" };
const string hundreds [] = { "" , "C" , "CC" , "CCC" , "CD" ,
"D" , "DC" , "DCC" , "DCCC" , "CM" };
const string tens [] = { "" , "X" , "XX" , "XXX" , "XL" ,
"L" , "LX" , "LXX" , "LXXX" , "XC" };
const string ones [] = { "" , "I" , "II" , "III" , "IV" ,
"V" , "VI" , "VII" , "VIII" , "IX" };
class Solution {
public:
string intToRoman ( int num ) {
int thousand = num / 1000 ;
int hundred = num % 1000 / 100 ;
int ten = num % 100 / 10 ;
int unit = num % 10 ;
return thousands [ thousand ] + hundreds [ hundred ] +
tens [ ten ] + ones [ unit ];
}
};
最后一个单词的长度 最后一个单词的长度
给你一个字符串 s,由若干单词组成,单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。
单词 是指仅由字母组成、不包含任何空格字符的最大子字符串。
示例 1:
输入:s = "Hello World"
输出:5
解释:最后一个单词是“World”,长度为 5。
示例 2:
输入:s = " fly me to the moon "
输出:4
解释:最后一个单词是“moon”,长度为 4。
示例 3:
输入:s = "luffy is still joyboy"
输出:6
解释:最后一个单词是长度为 6 的“joyboy”。
提示:
1 <= s.length <= 104
s 仅有英文字母和空格 ' ' 组成
s 中至少存在一个单词
思路1 kotlin速通 使用扩展函数可以光速解题:
class Solution {
fun lengthOfLastWord ( s : String ) = s . split ( " " ). filter { it . isNotEmpty ()}. last (). length
}
思路2 使用两个标记位记录位置 从后往前倒序遍历 ,记录下第一个有效非空字符和第一个有效字符之前的空格位置 ,计算二者差值即为长度;处理一下字符串一开始就是有效字符的边界情况。
class Solution {
public:
int lengthOfLastWord ( string s ) {
int n = s . size ();
int lastNotEmpty = - 1 ;
int lastSpaceBeforeString = - 1 ;
int size = 0 ;
for ( int i = n - 1 ; i >= 0 ; i -- ) {
if ( s [ i ] != ' ' && lastNotEmpty == - 1 ) {
lastNotEmpty = i ;
}
if ( s [ i ] == ' ' && lastNotEmpty != - 1 ) {
lastSpaceBeforeString = i ;
size = lastNotEmpty - lastSpaceBeforeString ;
break ;
}
// 处理开头就是有效位的情况
if ( i == 0 && lastSpaceBeforeString == - 1 ) {
size = lastNotEmpty + 1 ;
}
}
return size ;
}
};
最长公共前缀 最长公共前缀
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""。
示例 1:
输入:strs = ["flower","flow","flight"]
输出:"fl"
示例 2:
输入:strs = ["dog","racecar","car"]
输出:""
解释:输入不存在公共前缀。
提示:
1 <= strs.length <= 200
0 <= strs[i].length <= 200
strs[i] 如果非空,则仅由小写英文字母组成
思路1 水平扫描 从前往后遍历字符串数组中的每个字符串,对于每个遍历到的字符串,更新最长公共前缀,当遍历完所有的字符串以后,即可得到字符串数组中的最长公共前缀。
如果在尚未遍历完所有的字符串时,最长公共前缀已经是空串,则最长公共前缀一定是空串,因此不需要继续遍历剩下的字符串,直接返回空串即可。
class Solution {
public:
string longestCommonPrefix ( vector < string >& strs ) {
int n = strs . size ();
if ( n == 0 ) {
return "" ;
}
string longestPrefix = strs [ 0 ];
for ( int i = 1 ; i < n ; i ++ ) {
string commonPrefix = commonPrefixBetweenPair ( longestPrefix , strs [ i ]);
longestPrefix = commonPrefix ;
if ( longestPrefix == "" ) {
break ;
}
}
return longestPrefix ;
}
string commonPrefixBetweenPair ( string & s1 , string & s2 ) {
int n = min ( s1 . size (), s2 . size ());
int index = 0 ;
while ( index <= n && s1 [ index ] == s2 [ index ]) {
index ++ ;
}
return s1 . substr ( 0 , index );
}
};
151. 反转字符串中的单词 反转字符串中的单词
给你一个字符串 s ,请你反转字符串中 单词 的顺序。
单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。
注意:输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中,单词间应当仅用单个空格分隔,且不包含任何额外的空格。
示例 1:
输入:s = "the sky is blue"
输出:"blue is sky the"
示例 2:
输入:s = " hello world "
输出:"world hello"
解释:反转后的字符串中不能存在前导空格和尾随空格。
示例 3:
输入:s = "a good example"
输出:"example good a"
解释:如果两个单词间有多余的空格,反转后的字符串需要将单词间的空格减少到仅有一个。
提示:
1 <= s.length <= 104
s 包含英文大小写字母、数字和空格 ' '
s 中 至少存在一个 单词
进阶:如果字符串在你使用的编程语言中是一种可变数据类型,请尝试使用 O(1) 额外空间复杂度的 原地 解法。
kotlin 速通 先分割倒序,再插入空格拼接。
class Solution {
fun reverseWords ( s : String )= s . split ( " " ). filter { it . isNotEmpty ()}. reversed (). joinToString ( " " );
}
joinToString 用于将集合中的元素连接成一个字符串,返回一个新的字符串。可以指定连接符、前缀、后缀等。
思路1 拆出每一个单词填入一个新的数组,最后倒序遍历拼接 首先去除字符串首尾的空格,然后从前往后遍历字符串,找到每个单词的起始位置和结束位置,将每个单词填入一个新的数组,最后倒序遍历数组拼接单词即可。
class Solution {
public:
string reverseWords ( string s ) {
int n = s . size ();
vector < string > validateWords ( n );
int left = 0 ;
int right = n - 1 ;
string result = "" ;
// 去掉字符串开头的空白字符
while ( left <= right && s [ left ] == ' ' )
++ left ;
// 去掉字符串末尾的空白字符
while ( left <= right && s [ right ] == ' ' )
-- right ;
string word = "" ;
int count = 0 ;
// left指向第一个有效单次起始位置,right指向最后一个单词末尾位置
while ( left <= right ) {
char c = s [ left ];
if ( c != ' ' ) {
word += c ;
} else if ( word . size () > 0 && c == ' ' ) {
validateWords [ count ] = word ;
word = "" ;
count ++ ;
}
left ++ ;
}
validateWords [ count ] = word ;
count ++ ;
for ( int i = count - 1 ; i >= 0 ; i -- ) {
result += validateWords [ i ];
if ( i != 0 ) {
result += " " ;
}
}
return result ;
}
};
将存放单词的 vector 换成 stack 实现,可以不用维护 count 这个标记:
class Solution {
public:
string reverseWords ( string s ) {
int n = s . size ();
stack < string > validateWords ;
int left = 0 ;
int right = n - 1 ;
string result = "" ;
// 去掉字符串开头的空白字符
while ( left <= right && s [ left ] == ' ' )
++ left ;
// 去掉字符串末尾的空白字符
while ( left <= right && s [ right ] == ' ' )
-- right ;
string word = "" ;
// left指向第一个有效单次起始位置,right指向最后一个单词末尾位置
while ( left <= right ) {
char c = s [ left ];
if ( c != ' ' ) {
word += c ;
} else if ( word . size () > 0 && c == ' ' ) {
validateWords . push ( word );
word = "" ;
}
left ++ ;
}
validateWords . push ( word );
while ( ! validateWords . empty ()) {
result += validateWords . top ();
validateWords . pop ();
if ( ! validateWords . empty ()) {
result += " " ;
}
}
return result ;
}
};
思路2 直接操作原字符串 操作原字符串,先将整个字符串反转,然后在遍历的过程中,消减空格,将遇到的每个单词反转,最后去除末尾多余的空格。
class Solution {
public:
string reverseWords ( string s ) {
// 反转整个字符串
reverse ( s . begin (), s . end ());
int n = s . size ();
int idx = 0 ;
for ( int start = 0 ; start < n ; ++ start ) {
if ( s [ start ] != ' ' ) {
// 填一个空白字符然后将idx移动到下一个单词的开头位置
if ( idx != 0 ) s [ idx ++ ] = ' ' ;
// 循环遍历至单词的末尾
int end = start ;
while ( end < n && s [ end ] != ' ' ) s [ idx ++ ] = s [ end ++ ];
// 反转整个单词
reverse ( s . begin () + idx - ( end - start ), s . begin () + idx );
// 更新start,去找下一个单词
start = end ;
}
}
s . erase ( s . begin () + idx , s . end ());
return s ;
}
};
Z 字形变换 Z 字形变换
将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 "PAYPALISHIRING" 行数为 3 时,排列如下:
P A H N
A P L S I I G
Y I R
之后,你的输出需要从左往右逐行读取,产生出一个新的字符串,比如:"PAHNAPLSIIGYIR"。
请你实现这个将字符串进行指定行数变换的函数:
string convert(string s, int numRows);
示例 1:
输入:s = "PAYPALISHIRING", numRows = 3
输出:"PAHNAPLSIIGYIR"
示例 2:
输入:s = "PAYPALISHIRING", numRows = 4
输出:"PINALSIGYAHRPI"
解释:
P I N
A L S I G
Y A H R
P I
示例 3:
输入:s = "A", numRows = 1
输出:"A"
提示:
1 <= s.length <= 1000
s 由英文字母(小写和大写)、',' 和 '.' 组成
1 <= numRows <= 1000
官方题解 二维矩阵模拟
class Solution {
public:
string convert ( string s , int numRows ) {
int n = s . length (), r = numRows ;
if ( r == 1 || r >= n ) {
return s ;
}
int t = r * 2 - 2 ;
int c = ( n + t - 1 ) / t * ( r - 1 );
vector < string > mat ( r , string ( c , 0 ));
for ( int i = 0 , x = 0 , y = 0 ; i < n ; ++ i ) {
mat [ x ][ y ] = s [ i ];
if ( i % t < r - 1 ) {
++ x ; // 向下移动
} else {
-- x ;
++ y ; // 向右上移动
}
}
string ans ;
for ( auto & row : mat ) {
for ( char ch : row ) {
if ( ch ) {
ans += ch ;
}
}
}
return ans ;
}
};
思路1 顺序填入,控制转向 不用在意元素的处于转换矩阵中的哪一列,只需要关注元素的处于转换矩阵中的哪一行。 将字符串元素按照Z形填入,就是从上往下填到最后一行 (numRows - 1) 的元素就转向,从下往上填,等填到最上面一行 (0) 了,接下来就再往下。
class Solution {
public:
string convert ( string s , int numRows ) {
int n = s . size ();
if ( numRows == 1 || n < numRows ) {
return s ;
}
// 预存矩阵,存放每一行的结果
vector < string > rows ( numRows );
// 转向标志位,触底和触顶反弹
int trunFlag = 1 ;
int index = 0 ;
for ( int i = 0 ; i < n ; i ++ ) {
rows [ index ]. push_back ( s [ i ]);
// 更新下一个元素下标
index += trunFlag ;
// 达到转向条件,变向
if ( index == numRows - 1 || index == 0 ) {
trunFlag = - trunFlag ;
}
}
string result ;
for ( auto row : rows ) {
result += row ;
}
return result ;
}
};
找出字符串的第一个匹配项下标 找出字符串的第一个匹配项下标
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
示例 1:
输入:haystack = "sadbutsad", needle = "sad"
输出:0
解释:"sad" 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ,所以返回 0 。
示例 2:
输入:haystack = "leetcode", needle = "leeto"
输出:-1
解释:"leeto" 没有在 "leetcode" 中出现,所以返回 -1 。
提示:
1 <= haystack.length, needle.length <= 104
haystack 和 needle 仅由小写英文字符组成
思路1 借用找前缀那一题的思想 对 haystack 字符串进行遍历,找到第一个匹配的字符,判断以这个字符下标 i 为起始位置的子字符串是否和 needle 字符串为前缀重合的字符串。
将原问题简化为判断子字符串是否和 needle 字符串为前缀重合。
class Solution {
public:
int strStr ( string haystack , string needle ) {
int longLenth = haystack . size ();
int shortLenth = needle . size ();
// 长度判断,子串更长,直接判错
if ( longLenth < shortLenth ) {
return - 1 ;
}
for ( int i = 0 ; i < longLenth ; i ++ ) {
if ( haystack [ i ] == needle [ 0 ]) {
string cmp = haystack . substr ( i , longLenth - i );
// 找到公共前缀,返回下标
if ( findCommonPrefix ( cmp , needle )) {
return i ;
}
}
}
// 遍历完都没有找到公共前缀,返回-1
return - 1 ;
}
// 找公共前缀
bool findCommonPrefix ( string & s1 , string & s2 ) {
int n = s2 . size ();
for ( int i = 0 ; i < n ; i ++ ) {
if ( s1 [ i ] != s2 [ i ]) {
return false ;
}
}
return true ;
}
};
直接使用find函数 做完基础校验后,直接使用库函数 find 查找子字符串 needle 是否存在于 haystack 中。
class Solution {
public:
int strStr ( string haystack , string needle ) {
int longLenth = haystack . size ();
int shortLenth = needle . size ();
// 长度判断,子串更长,直接判错
if ( longLenth < shortLenth ) {
return - 1 ;
}
// 直接使用库函数
size_t pos = haystack . find ( needle );
if ( pos != string :: npos ) {
return pos ;
} else {
return - 1 ;
}
}
};
文本左右对齐 文本左右对齐
给定一个单词数组 words 和一个长度 maxWidth ,重新排版单词,使其成为每行恰好有 maxWidth 个字符,且左右两端对齐的文本。
你应该使用 “贪心算法” 来放置给定的单词;也就是说,尽可能多地往每行中放置单词。必要时可用空格 ' ' 填充,使得每行恰好有 maxWidth 个字符。
要求尽可能均匀分配单词间的空格数量。如果某一行单词间的空格不能均匀分配,则左侧放置的空格数要多于右侧的空格数。
文本的最后一行应为左对齐,且单词之间不插入额外的空格。
注意:
单词是指由非空格字符组成的字符序列。
每个单词的长度大于 0,小于等于 maxWidth。
输入单词数组 words 至少包含一个单词。
示例 1:
输入: words = ["This", "is", "an", "example", "of", "text", "justification."], maxWidth = 16
输出:
[
"This is an",
"example of text",
"justification. "
]
示例 2:
输入:words = ["What","must","be","acknowledgment","shall","be"], maxWidth = 16
输出:
[
"What must be",
"acknowledgment ",
"shall be "
]
解释: 注意最后一行的格式应为 "shall be " 而不是 "shall be",
因为最后一行应为左对齐,而不是左右两端对齐。
第二行同样为左对齐,这是因为这行只包含一个单词。
示例 3:
输入:words = ["Science","is","what","we","understand","well","enough","to","explain","to","a","computer.","Art","is","everything","else","we","do"],maxWidth = 20
输出:
[
"Science is what we",
"understand well",
"enough to explain to",
"a computer. Art is",
"everything else we",
"do "
]
提示:
1 <= words.length <= 300
1 <= words[i].length <= 20
words[i] 由小写英文字母和符号组成
1 <= maxWidth <= 100
words[i].length <= maxWidth
思路1 模拟
class Solution {
// blank 返回长度为 n 的由空格组成的字符串
string blank ( int n ) {
return string ( n , ' ' );
}
// join 返回用 sep 拼接 [left, right) 范围内的 words 组成的字符串
string join ( vector < string > & words , int left , int right , string sep ) {
string s = words [ left ];
for ( int i = left + 1 ; i < right ; ++ i ) {
s += sep + words [ i ];
}
return s ;
}
public:
vector < string > fullJustify ( vector < string > & words , int maxWidth ) {
vector < string > ans ;
int right = 0 , n = words . size ();
while ( true ) {
int left = right ; // 当前行的第一个单词在 words 的位置
int sumLen = 0 ; // 统计这一行单词长度之和
// 循环确定当前行可以放多少单词,注意单词之间应至少有一个空格
while ( right < n && sumLen + words [ right ]. length () + right - left <= maxWidth ) {
sumLen += words [ right ++ ]. length ();
}
// 当前行是最后一行:单词左对齐,且单词之间应只有一个空格,在行末填充剩余空格
if ( right == n ) {
string s = join ( words , left , n , " " );
ans . emplace_back ( s + blank ( maxWidth - s . length ()));
return ans ;
}
int numWords = right - left ;
int numSpaces = maxWidth - sumLen ;
// 当前行只有一个单词:该单词左对齐,在行末填充剩余空格
if ( numWords == 1 ) {
ans . emplace_back ( words [ left ] + blank ( numSpaces ));
continue ;
}
// 当前行不只一个单词
int avgSpaces = numSpaces / ( numWords - 1 );
int extraSpaces = numSpaces % ( numWords - 1 );
string s1 = join ( words , left , left + extraSpaces + 1 , blank ( avgSpaces + 1 )); // 拼接额外加一个空格的单词
string s2 = join ( words , left + extraSpaces + 1 , right , blank ( avgSpaces )); // 拼接其余单词
ans . emplace_back ( s1 + blank ( avgSpaces ) + s2 );
}
}
};
字符串表示的数字相加 415.字符串相加
给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和并同样以字符串形式返回。
你不能使用任何內建的用于处理大整数的库(比如 BigInteger), 也不能直接将输入的字符串转换为整数形式。
示例 1:
输入:num1 = "11", num2 = "123"
输出:"134"
示例 2:
输入:num1 = "456", num2 = "77"
输出:"533"
示例 3:
输入:num1 = "0", num2 = "0"
输出:"0"
提示:
1 <= num1.length, num2.length <= 104
num1 和num2 都只包含数字 0-9
num1 和num2 都不包含任何前导零
思路1 库函数 std::stoi() 函数可以将字符串转换为整数。 std::to_string() 函数可以将整数转换为字符串。
class Solution {
public:
string addStrings ( string num1 , string num2 ) {
return to_string ( stoi ( num1 ) + stoi ( num2 ));
}
};
在超出int范围会溢出。
模拟手工加法 从最低位到高位倒序遍历,对两个字符串数字的每一位进行加法运算,结果存储在一个新的字符串中。注意处理进位,超出10的进位在下一次遍历中加进去。
class Solution {
public:
string addStrings ( string num1 , string num2 ) {
int i = num1 . size () - 1 ;
int j = num2 . size () - 1 ;
int carry = 0 ;
string result = "" ;
// 从右往左逐位相加
while ( i >= 0 || j >= 0 || carry > 0 ) {
// 和字符0的ASCII值相减,得到当前位的数字int值
int digit1 = ( i >= 0 ) ? num1 [ i ] - '0' : 0 ;
int digit2 = ( j >= 0 ) ? num2 [ j ] - '0' : 0 ;
// 计算当前位的和,注意要加上上一次的进位
int sum = digit1 + digit2 + carry ;
carry = sum / 10 ; // 和大于10再进位
int current_digit = sum % 10 ; // 当前位取余数加到结果中
result . push_back ( current_digit + '0' );
i -- ;
j -- ;
}
// 反转结果字符串
reverse ( result . begin (), result . end ());
return result ;
}
};
最大子数组和 最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
提示:
1 <= nums.length <= 105
-104 <= nums[i] <= 104
进阶:如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的 分治法 求解。
思路1 动态规划 这题乍一看需要像是滑动窗口求解,但是数组无序,且不能改变元素顺序。所以无法判断滑动窗口的移动条件。
应该使用动态规划求解。
假设 nums 数组的长度是 n,下标从 0 到 n−1。
我们用 f(i) 代表以第 i 个数结尾的「连续子数组的最大和」,那么很显然我们要求的答案就是: \(\max_{0 \leq i \leq n-1} f(i)\)
因此我们只需要求出每个位置的 f(i),然后返回 f 数组中的最大值即可。 那么我们如何求 f(i) 呢? 我们可以考虑 nums[i] 单独成为一段还是加入 f(i−1) 对应的那一段,这取决于 nums[i] 和 f(i−1)+nums[i] 的大小,我们希望获得一个比较大的,于是可以写出这样的动态规划转移方程:
f(i)=max{f(i−1)+nums[i],nums[i]}
不难给出一个时间复杂度 O(n)、空间复杂度 O(n) 的实现,即用一个 f 数组来保存 f(i) 的值,用一个循环求出所有 f(i)。考虑到 f(i) 只和 f(i−1) 相关,于是我们可以只用一个变量 pre 来维护对于当前 f(i) 的 f(i−1) 的值是多少,从而让空间复杂度降低到 O(1),这有点类似 「滚动数组」 的思想。
class Solution {
public:
int maxSubArray ( vector < int >& nums ) {
int maxSum = nums [ 0 ];
int currentSum = nums [ 0 ];
for ( int i = 1 ; i < nums . size (); i ++ ) {
currentSum = max ( nums [ i ], currentSum + nums [ i ]);
maxSum = max ( maxSum , currentSum );
}
return maxSum ;
}
};
字母异位词分组 字母异位词分组
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
示例 1:
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
解释:
在 strs 中没有字符串可以通过重新排列来形成 "bat"。
字符串 "nat" 和 "tan" 是字母异位词,因为它们可以重新排列以形成彼此。
字符串 "ate" ,"eat" 和 "tea" 是字母异位词,因为它们可以重新排列以形成彼此。
示例 2:
输入: strs = [""]
输出: [[""]]
示例 3:
输入: strs = ["a"]
输出: [["a"]]
提示:
1 <= strs.length <= 104
0 <= strs[i].length <= 100
strs[i] 仅包含小写字母
思路1 hash表对比 每个元素都是一个字符串,如果两个元素是互为异位词,这两个字符串排序之后的结果一定相同,可以将排序后的结果设为 key ,value就为一个string的动态数组,有相同的直接推送到value里面。最后取出来加入到结果数组里。
class Solution {
public:
vector < vector < string >> groupAnagrams ( vector < string >& strs ) {
int n = strs . size ();
// 最终结果
vector < vector < string >> ans ;
// 用来对比的hash表
unordered_map < string , vector < string >> mp ;
for ( string & str : strs ) {
string key = str ;
sort ( key . begin (), key . end ());
// 排序后的字符串作为key,互为异位词的元素全部加进去
mp [ key ]. emplace_back ( str );
}
// 遍历hash表,填到结果数组里
for ( auto it = mp . begin (); it != mp . end (); it ++ ) {
ans . emplace_back ( it -> second );
}
return ans ;
}
};
数组和字符串算法题总结 无论是数组还是字符串,在算法题中,它们本质上都是线性的数据结构 。字符串可以看作是一个字符数组,因此很多数组的技巧同样适用于字符串。解题的核心在于高效地遍历和操作这些线性序列 。
一、数组常见题型与解法 1. 双指针技巧 这是解决数组问题最常用、最核心的技巧之一,变化多端。
对撞指针 :两个指针从两端向中间移动。适用场景 :有序数组的二分查找。 两数之和、三数之和问题(当数组有序时)。 反转数组、判断回文。 示例 :在一个有序数组中找出两个数,使它们的和为 target。快慢指针 :两个指针以不同速度移动。适用场景 :判断链表是否有环(同样适用于数组的循环查找)。 原地删除有序数组中的重复项(LeetCode 26)。 移动零(LeetCode 283),将0移到数组末尾而不改变非零元素的相对顺序。 示例 :slow 指针指向下一个非零元素该放的位置,fast 指针遍历数组。滑动窗口 :双指针的一种特殊形式,维护一个窗口(子数组),通过移动左右指针来动态调整窗口大小。适用场景 :寻找满足条件的最长/最短子数组 或子字符串 。 求和/乘积大于/小于某值的子数组个数。 关键 :思考窗口何时扩大(右指针右移),何时收缩(左指针右移),以及如何更新结果。示例 :无重复字符的最长子串(LeetCode 3)、长度最小的子数组(LeetCode 209)。2. 前缀和 用于快速、频繁地计算子数组的区间和 。
核心思想 :预处理一个 prefix 数组,其中 prefix[i] 表示 nums[0] 到 nums[i-1] 的和(或 nums[0] 到 nums[i],看定义)。适用场景 :求任意区间 [i, j] 的和,公式为 prefix[j+1] - prefix[i]。 统计满足“子数组和为k”的子数组个数(常配合哈希表使用,记录前缀和出现的次数)。 示例 :和为 K 的子数组(LeetCode 560)。3. 模拟与数学 这类问题更考验对题意的理解和代码实现能力。
适用场景 :矩阵/二维数组的螺旋遍历(LeetCode 54)。 数组的旋转(LeetCode 189),常用多次反转的技巧。 下一个排列(LeetCode 31)。 寻找主元素(出现次数超过一半的元素,摩尔投票法)。 4. 哈希表 利用 std::unordered_map 或 std::unordered_set 实现 O(1) 时间复杂度的查找,是“空间换时间”的典范。
适用场景 :两数之和(LeetCode 1)的经典解法。 判断数组中是否存在重复元素。 与前缀和结合,解决“子数组和为k”的问题。 统计元素频率。 二、字符串常见题型与解法 字符串的很多技巧与数组相通,但也有其特殊性(如反转、子串匹配等)。
1. 双指针 适用场景 :判断回文串。 反转字符串(LeetCode 344)。 字符串压缩。 2. 滑动窗口 适用场景 :字符串的经典问题 :无重复字符的最长子串(LeetCode 3)。找到字符串中所有字母异位词(LeetCode 438)。 最小覆盖子串(LeetCode 76)。 3. 字符串匹配 - KMP 算法 用于解决子串查找 问题。
核心思想 :当匹配失败时,利用已匹配的信息(next数组/前缀表)跳过不必要的比较,将指针回退到合理的位置。适用场景 :判断一个字符串是否是另一个字符串的子串。 重复的子字符串问题(LeetCode 459)。 4. 字符串操作与模拟 适用场景 :字符串转换整数 (atoi)(LeetCode 8)。 验证IP地址(LeetCode 468)。 字符串解码(LeetCode 394),常用栈来解决。 翻转字符串里的单词(LeetCode 151),综合运用反转和双指针。 5. 哈希表与计数 适用场景 :有效的字母异位词(LeetCode 242)。 找到所有字母异位词的起始索引(可与滑动窗口结合)。 第一个只出现一次的字符。 三、通用解题思路与技巧 排序是利器 :很多复杂问题在排序后会变得简单(例如,双指针解决多数和问题)。但要注意排序是否会改变原始索引。空间换时间 :毫不犹豫地使用哈希表、辅助数组等来存储中间结果,这是优化时间复杂度的常用手段。边界条件 :数组/字符串为空、只有一个元素、所有元素相同等特殊情况一定要考虑。STL 的熟练运用 :vector: 动态数组,最常用。string: 提供了 find, substr 等方法,但要注意效率。unordered_map / unordered_set: 高效的哈希容器。stack / queue: 用于特定场景,如单调栈解决“下一个更大元素”问题。复杂度分析 :养成分析时间、空间复杂度的习惯,这有助于你选择最优解法。总结表格 类别 常见题型 核心解决方式 数组 两数/三数之和、子数组和 排序+双指针、哈希表、前缀和 子数组问题(最大和、满足条件) 滑动窗口、前缀和、动态规划(如最大子数组和) 去重、移动元素 快慢指针 旋转、螺旋矩阵 模拟、数学技巧(多次反转) 字符串 回文、反转 双指针 无重复最长子串、字母异位词 滑动窗口 子串查找/匹配 KMP算法 字符串解析、解码 模拟、栈 异位词判断、字符计数 哈希表
最后建议 :理论学习后,一定要去 LeetCode 或类似平台进行专题练习,将这些技巧内化为自己的解题能力。可以从“Top 100 Liked”问题列表开始,里面包含了大量数组和字符串的经典题目。
合并两个有序链表 合并两个有序链表
将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例 1:
输入:l1 = [1,2,4], l2 = [1,3,4]
输出:[1,1,2,3,4,4]
示例 2:
输入:l1 = [], l2 = []
输出:[]
示例 3:
输入:l1 = [], l2 = [0]
输出:[0]
提示:
• 两个链表的节点数目范围是 [0, 50]
• -100 <= Node.val <= 100
• l1 和 l2 均按 非递减顺序 排列
思路 将其当作模拟题,新建一个头,将两个链表挨个遍历,比较大小,将较小的一个添加进新链表,再往后移动。
class Solution {
public:
ListNode * mergeTwoLists ( ListNode * list1 , ListNode * list2 ) {
ListNode * p = list1 ;
ListNode * q = list2 ;
if ( p == nullptr ){
return q ;
}
if ( q == nullptr ){
return p ;
}
// 选定p为基准
ListNode * newHead = new ListNode ( 0 , nullptr );
ListNode * x = newHead ;
while ( p != nullptr || q != nullptr ){
if ( p != nullptr ){
if ( q == nullptr || p -> val <= q -> val ){
x -> next = p ;
p = p -> next ;
x = x -> next ;
}
}
if ( q != nullptr ){
if ( p == nullptr || q -> val < p -> val ){
x -> next = q ;
q = q -> next ;
x = x -> next ;
}
}
}
return newHead -> next ;
}
};
官方题解 使用递归算法,设置一个比较函数,同时判断两个链表的头,每次都将更小的节点的next保留,再次调用比较函数,最后一层一层返回这个结果。也就是说,两个链表头部值较小的一个节点与剩下元素的 merge 操作结果合并。
我们直接将以上递归过程建模,同时需要考虑边界情况。 如果 l1 或者 l2 一开始就是空链表 ,那么没有任何操作需要合并,所以我们只需要返回非空链表。否则,我们要判断 l1 和 l2 哪一个链表的头节点的值更小,然后递归地决定下一个添加到结果里的节点。如果两个链表有一个为空,递归结束。
ListNode * mergeTwoLists ( ListNode * list1 , ListNode * list2 ) {
// list1已经遍历完,剩下的list2为更大的数字,直接加在尾部
if ( list1 == nullptr ) {
return list2 ;
} else if ( list2 == nullptr ) {
return list1 ;
} else if ( list1 -> val < list2 -> val ) {
// list1的值更小,保留list1这个元素的next指针,指向后面的更大的元素
list1 -> next = mergeTwoLists ( list1 -> next , list2 );
return list1 ;
} else {
list2 -> next = mergeTwoLists ( list1 , list2 -> next );
return list2 ;
}
}
找到两个相交链表的交点节点 找到两个相交链表的交点节点
给定两个单链表的头节点 headA 和 headB ,请找出并返回两个单链表相交的起始节点。如果两个链表没有交点,返回 null 。
图示两个链表在节点 c1 开始相交:
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须保持其原始结构 。
示例 1:
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出:Intersected at '8'
解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,0,1,8,4,5]。
在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。
示例 2:
输入:intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出:Intersected at '2'
解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。
从各自的表头开始算起,链表 A 为 [0,9,1,2,4],链表 B 为 [3,2,4]。
在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。
示例 3:
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出:null
解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。
由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。
这两个链表不相交,因此返回 null 。
思路1 判断共尾节点计算差值 先判断二者中有无空链表;两个链表相交必是同一个尾节点;计算是否共尾节点,同时计算出各自的长度,比较出长度差,将较长的那个先移动这个差值的距离,然后两个链表再一起移动,两个指针就会慢慢指向同节点,判断相等了返回即可。
class Solution {
public:
ListNode * getIntersectionNode ( ListNode * headA , ListNode * headB ) {
if ( headA == nullptr || headB == nullptr ){
return nullptr ;
}
ListNode * p = headA ;
ListNode * q = headB ;
int lenthA = 0 ;
int lenthB = 0 ;
while ( p -> next != nullptr ) {
p = p -> next ;
lenthA ++ ;
}
while ( q -> next != nullptr ) {
q = q -> next ;
lenthB ++ ;
}
if ( p != q ){
return nullptr ;
}
p = headA ;
q = headB ;
if ( lenthA > lenthB ){
int diff = lenthA - lenthB ;
while ( diff > 0 ){
p = p -> next ;
diff -- ;
}
}
if ( lenthA < lenthB ){
int diff = lenthB - lenthA ;
while ( diff > 0 ){
q = q -> next ;
diff -- ;
}
}
while ( p != q ){
p = p -> next ;
q = q -> next ;
}
return p ;
}
};
思路2 hash集合 unordered_set 判断两个链表是否相交,可以使用哈希集合存储链表节点。
首先遍历链表 headA,并将链表 headA 中的每个节点加入哈希集合中。然后遍历链表 headB,对于遍历到的每个节点,判断该节点是否在哈希集合中:
如果当前节点不在哈希集合中,则继续遍历下一个节点;
如果当前节点在哈希集合中,则后面的节点都在哈希集合中,即从当前节点开始的所有节点都在两个链表的相交部分,因此 在链表 headB 中遍历到的第一个在哈希集合中的节点就是两个链表相交的节点,返回该节点 。
如果链表 headB 中的所有节点都不在哈希集合中,则两个链表不相交,返回 null。
class Solution {
public:
ListNode * getIntersectionNode ( ListNode * headA , ListNode * headB ) {
unordered_set < ListNode *> visited ;
ListNode * temp = headA ;
while ( temp != nullptr ) {
visited . insert ( temp );
temp = temp -> next ;
}
temp = headB ;
while ( temp != nullptr ) {
if ( visited . count ( temp )) {
return temp ;
}
temp = temp -> next ;
}
return nullptr ;
}
};
翻转链表 翻转链表
给定单链表的头节点 head ,请反转链表,并返回反转后的链表的头节点。
示例 1:
输入:head = [1,2,3,4,5]
输出:[5,4,3,2,1]
示例 2:
输入:head = [1,2]
输出:[2,1]
示例 3:
输入:head = []
输出:[]
提示:
• 链表中节点的数目范围是 [0, 5000]
• -5000 <= Node.val <= 5000
进阶:链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题?
思路 使用栈来暂存所有数据,出栈的时候新建一个头节点,来创建逆序链表。
使用 stack 容器处理,空间复杂度O(n)
ListNode * reverseList ( ListNode * head ) {
stack < int > temp ;
ListNode * p = head ;
while ( p != nullptr ){
cout << "value: " << p -> val << endl ;
temp . push ( p -> val );
p = p -> next ;
}
ListNode * newHead = new ListNode ();
ListNode * q = newHead ;
while ( ! temp . empty ()){
cout << "stack value: " << temp . top () << endl ;
ListNode * tempNode = new ListNode ( temp . top ());
q -> next = tempNode ;
q = q -> next ;
temp . pop ();
}
return newHead -> next ;
}
思路2 官方题解,遍历链表,使用两个指针来保存当前值和上一个的值,同时在循环中需要暂时存储下一个节点地址,防止断链。 循环时,将当前节点的next节点的next指针指向当前节点,当前节点的next指针指向上一个节点,然后当前节点和上一个节点都往后走。
// 只用了两个变量,空间复杂度 O(1)
ListNode * reverseList2 ( ListNode * head ) {
ListNode * current = head ;
ListNode * prev = nullptr ;
while ( current != nullptr ) {
ListNode * next = current -> next ;
current -> next = prev ;
prev = current ;
current = next ;
}
return prev ;
}
思路3 官方的递归解法 递归版本稍微复杂一些,其关键在于反向工作。假设链表的其余部分已经被反转,现在应该如何反转它前面的部分?
假设链表为: n1 →…→ nk−1 → nk → nk+1 →…→ nm →∅
若从节点 nk+1 到 nm 已经被反转,而我们正处于 nk 。
n1 →…→ nk−1 → nk →nk+1 ←…← nm
我们希望 nk+1 的下一个节点指向 nk。
所以,nk.next.next=nk 。需要注意的是 n1 的下一个节点必须指向 ∅。如果忽略了这一点,链表中可能会产生环.
class Solution {
public:
ListNode * reverseList ( ListNode * head ) {
if ( ! head || ! head -> next ) {
return head ;
}
ListNode * newHead = reverseList ( head -> next );
head -> next -> next = head ;
head -> next = nullptr ;
return newHead ;
}
};
翻转链表2 翻转链表2
给你单链表的头指针 head 和两个整数 left 和 right ,其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点,返回 反转后的链表 。
示例 1:
输入:head = [1,2,3,4,5], left = 2, right = 4
输出:[1,4,3,2,5]
示例 2:
输入:head = [5], left = 1, right = 1
输出:[5]
提示:
• 链表中节点数目为 n
• 1 <= n <= 500
• -500 <= Node.val <= 500
• 1 <= left <= right <= n
进阶: 你可以使用一趟扫描完成反转吗?
思路1 掐断 翻转 拼接 将要反转的区间掐断,采用上一题的方法来翻转,关键 提前存储好区间左侧和右侧的第一个节点 ,方便再拼接回去,但是注意这里可能并没有前一个节点,所以加一个虚拟头节点,来承接翻转后的区间,免去多余判断。区间右侧的第一个节点为nullptr没有关系。
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode * reverseList ( ListNode * head ) {
ListNode * current = head ;
ListNode * priv = nullptr ;
while ( current != nullptr ) {
ListNode * next = current -> next ;
current -> next = priv ;
priv = current ;
current = next ;
}
return priv ;
}
ListNode * reverseBetween ( ListNode * head , int left , int right ) {
if ( left == right ) {
return head ;
}
ListNode * dummyHead = new ListNode ( - 1 );
dummyHead -> next = head ;
ListNode * p = dummyHead ;
ListNode * q = dummyHead ;
ListNode * first ;
ListNode * last ;
for ( int i = 0 ; i < left - 1 ; i ++ ) {
p = p -> next ;
}
first = p -> next ;
for ( int j = 0 ; j < right ; j ++ ) {
q = q -> next ;
}
last = q ;
// 将q移到区间外第一个元素位置
q = q -> next ;
p -> next = last ;
last -> next = nullptr ;
ListNode * corridor = reverseList ( first );
while ( corridor -> next != nullptr ) {
corridor = corridor -> next ;
}
corridor -> next = q ;
return dummyHead -> next ;
}
};
思路2 穿针引线 方法一的缺点是:如果 left 和 right 的区域很大,恰好是链表的头节点和尾节点时,找到 left 和 right 需要遍历一次,反转它们之间的链表还需要遍历一次,虽然总的时间复杂度为 O(N),但 遍历了链表 2 次 ,可不可以只遍历一次呢?答案是可以的。
在需要反转的区间里,每遍历到一个节点,让这个新节点来到反转部分的起始位置。下面的图展示了整个流程。
初始链表:9->7->2->5->4->3->6 第一步将5插到2的前面,第二步将4插到2的前面。。。
使用三个指针变量 pre、curr、next 来记录反转的过程中需要的变量,它们的意义如下:
curr:指向待反转区域的第一个节点 left; next:永远指向 curr 的下一个节点,循环过程中,curr 变化以后 next 会变化; pre:永远指向待反转区域的第一个节点 left 的前一个节点,在循环过程中不变。 class Solution {
public:
ListNode * reverseBetween ( ListNode * head , int left , int right ) {
// 设置虚拟头节点,用于处理头节点可能被翻转的情况
// 这是处理链表问题的常用技巧,可以避免对头节点的特殊处理
ListNode * dummyNode = new ListNode ( - 1 );
dummyNode -> next = head ;
// pre指针指向要翻转区间的前一个节点
// 通过循环将pre移动到left位置的前一个节点
ListNode * pre = dummyNode ;
for ( int i = 0 ; i < left - 1 ; i ++ ) {
pre = pre -> next ;
}
// cur指针指向当前要处理的节点(翻转区间的第一个节点)
ListNode * cur = pre -> next ;
ListNode * next ; // 用于临时存储下一个要处理的节点
// 进行区间内的节点翻转
// 循环次数为区间长度减1(right - left)
for ( int i = 0 ; i < right - left ; i ++ ) {
// next指向cur的下一个节点(即要移动到前面的节点)
next = cur -> next ;
// 将cur指向next的下一个节点,跳过next节点
cur -> next = next -> next ;
// 将next节点插入到pre节点的后面
next -> next = pre -> next ;
// 更新pre的next指针,指向新插入到前面的next节点
pre -> next = next ;
}
// 返回虚拟头节点的下一个节点(即新的头节点)
return dummyNode -> next ;
}
};
翻转链表3(k个一组) K 个一组翻转链表
给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。
k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
示例 1:
输入:head = [1,2,3,4,5], k = 2
输出:[2,1,4,3,5]
示例 2:
输入:head = [1,2,3,4,5], k = 3
输出:[3,2,1,4,5]
提示:
• 链表中的节点数目为 n
• 1 <= k <= n <= 5000
• 0 <= Node.val <= 1000
进阶:你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗?
思路 基于 1 & 2 版本,更需要控制好每一组之间的链接,尤其是循环后的翻转和善后工作。
记录了区间的头尾,区间的上一个,还有区间的下一个,用于断链后重新链接翻转后的区间。有别于官方题解,本地编译器用不了pair等C++11以后的库,所以区间翻转后,是通过移动区间头指针来找到翻转后的区间尾节点,来链接下一个点的。
class Solution {
public:
ListNode * reverseList ( ListNode * head )
{
ListNode * current = head ;
ListNode * priv = nullptr ;
while ( current != nullptr )
{
ListNode * next = current -> next ;
current -> next = priv ;
priv = current ;
current = next ;
}
return priv ;
}
ListNode * reverseKGroup ( ListNode * head , int k )
{
ListNode * dummyHead = new ListNode ( - 1 );
dummyHead -> next = head ;
ListNode * priv ;
ListNode * p = dummyHead ;
while ( p != nullptr )
{
priv = p ;
ListNode * reverseHead = priv -> next ;
for ( int i = 0 ; i < k ; i ++ )
{
p = p -> next ;
if ( p == nullptr )
{
return dummyHead -> next ;
}
}
ListNode * reverseTail = p ;
ListNode * nextNode = p -> next ;
reverseTail -> next = nullptr ;
ListNode * reversed = reverseList ( reverseHead );
priv -> next = reversed ;
while ( reversed -> next != nullptr )
{
reversed = reversed -> next ;
}
p = reversed ;
reversed -> next = nextNode ;
}
return dummyHead -> next ;
}
};
复制带随机指针的链表 复制带随机指针的链表
给你一个长度为 n 的链表,每个节点包含一个额外增加的随机指针 random ,该指针可以指向链表中的任何节点或空节点。
构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成,其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点,并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。
例如,如果原链表中有 X 和 Y 两个节点,其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ,同样有 x.random --> y 。
返回复制链表的头节点。
用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示:
val:一个表示 Node.val 的整数。
random_index:随机指针指向的节点索引(范围从 0 到 n-1);如果不指向任何节点,则为 null 。
你的代码 只 接受原链表的头节点 head 作为传入参数。
示例 1:
输入:head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出:[[7,null],[13,0],[11,4],[10,2],[1,0]]
示例 2:
输入:head = [[1,1],[2,1]]
输出:[[1,1],[2,1]]
示例 3:
输入:head = [[3,null],[3,0],[3,null]]
输出:[[3,null],[3,0],[3,null]]
提示:
• 0 <= n <= 1000
• -104 <= Node.val <= 104
• Node.random 为 null 或指向链表中的节点。
思路1 使用一个map,键为原始链表节点 A ,值为新建的节点 A’ ,在遍历原始链表的时候,看看原始节点的指针指向了哪里,通过map寻找对应节点key的value,就可以完全复制。
class Solution {
public:
Node * copyRandomList ( Node * head ) {
unordered_map < Node * , Node *> nodeMap ;
Node * p = head ;
while ( p != nullptr ){
nodeMap [ p ] = new Node ( p -> val );
p = p -> next ;
}
p = head ;
while ( p != nullptr ){
// 映射的next等于next的映射
nodeMap [ p ] -> next = nodeMap [ p -> next ];
nodeMap [ p ] -> random = nodeMap [ p -> random ];
p = p -> next ;
}
return nodeMap [ head ];
}
};
缺点:
使用了多一个的map空间,需要遍历两次,先添加一次,再根据映射关系来设置指向关系。
官方优化 一样使用了哈希表,但是使用了回溯算法,在第一个节点检查时就去创建指向的两个节点,如果为未创建过就新建一个填进map,如果已创建就不能再刷新value来了,而是直接复用这个值。少遍历了一遍执行时间从11ms,优化到了8ms。
class Solution {
public:
unordered_map < Node * , Node *> cachedNode ;
Node * copyRandomList ( Node * head ) {
if ( head == nullptr ) {
return nullptr ;
}
if ( ! cachedNode . count ( head )) {
Node * headNew = new Node ( head -> val );
cachedNode [ head ] = headNew ;
headNew -> next = copyRandomList ( head -> next );
headNew -> random = copyRandomList ( head -> random );
}
return cachedNode [ head ];
}
};
思路2 以上空间复杂度O(n),需要额外使用一个大map来存储节点,我们可以将新节点挨个插到每一个原始节点中间,然后遍历的时候,使用该节点指向原始节点的next指针来寻找刚刚新建的新节点,最后将新节点剥离出来,同时保证原链表正确还原(题目没有提这一点,但是检查的时候应该是需要用到原链表)
Node * copyRandomList ( Node * head )
{
// 长度为0
if ( head == nullptr )
{
return nullptr ;
}
Node * p = head ;
// 添加复制节点
while ( p )
{
Node * next = p -> next ;
Node * copyNode = new Node ( p -> val );
p -> next = copyNode ;
copyNode -> next = next ;
p = p -> next -> next ;
}
// 复制各个节点random指针
p = head ;
while ( p )
{
Node * copyNode = p -> next ;
if ( p -> random == nullptr )
{
copyNode -> random = nullptr ;
}
else
{
copyNode -> random = p -> random -> next ;
}
p = p -> next -> next ;
}
// 链表分离出来之后,next指针自动正确了
p = head ;
Node * ans = head -> next ;
Node * q = head -> next ;
// 当q已经触底,遍历到了最后一个
while ( q -> next != nullptr )
{
Node * copyNode = q -> next -> next ;
Node * originNode = p -> next -> next ;
q -> next = copyNode ;
p -> next = originNode ;
q = copyNode ;
p = originNode ;
}
// 目前两个链表是共尾节点的状态
// 掐断原始链表的指向复制链表的最后一个节点
p -> next = nullptr ;
return ans ;
}
判断环形链表 判断环形链表
给你一个链表的头节点 head ,判断链表中是否有环。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。
如果链表中存在环 ,则返回 true 。 否则,返回 false 。
示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:true
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
输入:head = [1,2], pos = 0
输出:true
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1
输出:false
解释:链表中没有环。
提示:
• 链表中节点的数目范围是 [0, 104]
• -105 <= Node.val <= 105
• pos 为 -1 或者链表中的一个 有效索引 。
进阶:你能用 O(1)(即,常量)内存解决此问题吗?
思路1 使用不可存在相同元素的set数据结构来存储每个节点的next地址,如果有相同的节点地址已经出现过,则说明有环,否则无环;
class Solution {
public:
bool hasCycle ( ListNode * head ) {
set < ListNode *> tempset ;
ListNode * p = head ;
tempset . insert ( head );
while ( p != nullptr ) {
if ( tempset . count ( p -> next ) > 0 ) {
return true ;
}
tempset . insert ( p -> next );
p = p -> next ;
}
return false ;
}
};
这种方法空间复杂度为O(n),执行时长也排到了末尾;
思路2 使用快慢指针,快指针一次走两个,慢指针一次走一个,如果能碰到一起,说明肯定有环存在;
bool hasCycle2 ( ListNode * head )
{
ListNode * fast = head ;
ListNode * slow = head ;
while ( slow != nullptr && fast != nullptr && fast -> next != nullptr )
{
slow = slow -> next ;
fast = fast -> next -> next ;
if ( slow == fast )
{
return true ;
}
}
return false ;
}
优化 while中使用三个判断条件,发现耗时有点长,将快指针的next空判断移到循环内部,可以进一步减少耗时。
class Solution {
public:
bool hasCycle ( ListNode * head ) {
ListNode * fast = head ;
ListNode * slow = head ;
while ( slow != nullptr && fast != nullptr ) {
if ( fast -> next != nullptr ) {
slow = slow -> next ;
fast = fast -> next -> next ;
if ( slow == fast ) {
return true ;
}
} else {
return false ;
}
}
return false ;
}
};
找到环形链表的入环节点 找到环形链表的入环节点
给定一个链表,返回链表开始入环的第一个节点。 从链表的头节点开始沿着 next 指针进入环的第一个节点为环的入口节点。如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。注意,pos 仅仅是用于标识环的情况,并不会作为参数传递到函数中。
说明:不允许修改给定的链表。
示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
输入:head = [1,2], pos = 0
输出:返回索引为 0 的链表节点
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1
输出:返回 null
解释:链表中没有环。
提示:
• 链表中节点的数目范围在范围 [0, 104] 内
• -105 <= Node.val <= 105
• pos 的值为 -1 或者链表中的一个有效索引
进阶:是否可以使用 O(1) 空间解决此题?
思路 还是使用set,当判断存在相同的地址时,直接返回这个节点地址即可。
class Solution {
public:
ListNode * detectCycle ( ListNode * head ) {
set < ListNode *> tempset ;
ListNode * p = head ;
tempset . insert ( head );
while ( p != nullptr ) {
if ( tempset . count ( p -> next ) > 0 ) {
return p -> next ;
}
tempset . insert ( p -> next );
p = p -> next ;
}
return nullptr ;
}
};
同样多创建了一个空间来存储地址
思路2 这个只需完整记忆,证明过程太复杂。使用快慢指针,当他们相遇时,将快指针还原到头节点。而后,快指针也变成一次跳一步,继续循环,当快慢指针第二次相遇时,就是在入环的节点位置。
class Solution {
public:
ListNode * detectCycle2 ( ListNode * head ) {
ListNode * fast = head ;
ListNode * slow = head ;
int meet_count = 0 ;
while ( fast != nullptr && slow != nullptr ) {
if ( fast -> next != nullptr ) {
slow = slow -> next ;
if ( meet_count == 0 ) {
fast = fast -> next -> next ;
if ( slow == fast ) {
fast = head ;
meet_count ++ ;
}
} else {
fast = fast -> next ;
if ( slow == fast ) {
return fast ;
}
}
} else {
return nullptr ;
}
}
return nullptr ;
}
};
在两个节点互相循环时有问题,可以说是互为入口,index是0,算出来是1.
链表排序 链表排序
给定链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。
示例 1:
输入:head = [4,2,1,3]
输出:[1,2,3,4]
示例 2:
输入:head = [-1,5,3,4,0]
输出:[-1,0,3,4,5]
示例 3:
输入:head = []
输出:[]
提示:
• 链表中节点的数目在范围 [0, 5 * 104] 内
• -105 <= Node.val <= 105
进阶:你可以在 O(nlogn) 时间复杂度和常数级空间复杂度下,对链表进行排序吗?
思路1 使用multiset,可以添加重复元素,可以自动排序。
class Solution
{
public:
ListNode * sortList ( ListNode * head )
{
if ( head == nullptr )
{
return head ;
}
multiset < int > sort_set ;
ListNode * p = head ;
while ( p != nullptr )
{
sort_set . insert ( p -> val );
p = p -> next ;
}
auto iterator = sort_set . begin ();
ListNode * newHead = new ListNode ( * iterator );
p = newHead ;
iterator ++ ;
while ( iterator != sort_set . end ())
{
ListNode * node = new ListNode ( * iterator );
p -> next = node ;
p = p -> next ;
iterator ++ ;
}
return newHead ;
}
};
性能较差
思路2 自上而下归并排序,不断二分,等颗粒度为1时,使用merge合并两个有序链表(长度为1一定有序),将所有的小链表 merge() 连接起来,最后合成一个大的。
class Solution {
public:
ListNode * sortList ( ListNode * head ) {
return sortList ( head , nullptr );
}
ListNode * sortList ( ListNode * head , ListNode * tail ) {
if ( head == nullptr ) {
return head ;
}
if ( head -> next == tail ) {
head -> next = nullptr ;
return head ;
}
ListNode * slow = head , * fast = head ;
while ( fast != tail ) {
slow = slow -> next ;
fast = fast -> next ;
if ( fast != tail ) {
fast = fast -> next ;
}
}
ListNode * mid = slow ;
return merge ( sortList ( head , mid ), sortList ( mid , tail ));
}
ListNode * merge ( ListNode * head1 , ListNode * head2 ) {
ListNode * dummyHead = new ListNode ( 0 );
ListNode * temp = dummyHead , * temp1 = head1 , * temp2 = head2 ;
while ( temp1 != nullptr && temp2 != nullptr ) {
if ( temp1 -> val <= temp2 -> val ) {
temp -> next = temp1 ;
temp1 = temp1 -> next ;
} else {
temp -> next = temp2 ;
temp2 = temp2 -> next ;
}
temp = temp -> next ;
}
if ( temp1 != nullptr ) {
temp -> next = temp1 ;
} else if ( temp2 != nullptr ) {
temp -> next = temp2 ;
}
return dummyHead -> next ;
}
};
时间复杂度:O(nlogn),其中 n 是链表的长度。 空间复杂度:O(logn),其中 n 是链表的长度。空间复杂度主要取决于递归调用的栈空间。
思路3 自下而上归并排序,步长为1,遍历排序,步长为2,再次排序。
class Solution {
public:
ListNode * sortList ( ListNode * head ) {
if ( head == nullptr ) {
return head ;
}
int length = 0 ;
ListNode * node = head ;
while ( node != nullptr ) {
length ++ ;
node = node -> next ;
}
ListNode * dummyHead = new ListNode ( 0 , head );
for ( int subLength = 1 ; subLength < length ; subLength <<= 1 ) {
ListNode * prev = dummyHead , * curr = dummyHead -> next ;
while ( curr != nullptr ) {
ListNode * head1 = curr ;
for ( int i = 1 ; i < subLength && curr -> next != nullptr ; i ++ ) {
curr = curr -> next ;
}
ListNode * head2 = curr -> next ;
curr -> next = nullptr ;
curr = head2 ;
for ( int i = 1 ; i < subLength && curr != nullptr && curr -> next != nullptr ; i ++ ) {
curr = curr -> next ;
}
ListNode * next = nullptr ;
if ( curr != nullptr ) {
next = curr -> next ;
curr -> next = nullptr ;
}
ListNode * merged = merge ( head1 , head2 );
prev -> next = merged ;
while ( prev -> next != nullptr ) {
prev = prev -> next ;
}
curr = next ;
}
}
return dummyHead -> next ;
}
ListNode * merge ( ListNode * head1 , ListNode * head2 ) {
ListNode * dummyHead = new ListNode ( 0 );
ListNode * temp = dummyHead , * temp1 = head1 , * temp2 = head2 ;
while ( temp1 != nullptr && temp2 != nullptr ) {
if ( temp1 -> val <= temp2 -> val ) {
temp -> next = temp1 ;
temp1 = temp1 -> next ;
} else {
temp -> next = temp2 ;
temp2 = temp2 -> next ;
}
temp = temp -> next ;
}
if ( temp1 != nullptr ) {
temp -> next = temp1 ;
} else if ( temp2 != nullptr ) {
temp -> next = temp2 ;
}
return dummyHead -> next ;
}
};
时间复杂度:O(nlogn),其中 n 是链表的长度。 空间复杂度:O(1)。
回文链表判断 回文链表判断
给定一个链表的 头节点 head ,请判断其是否为回文链表。
如果一个链表是回文,那么链表节点序列从前往后看和从后往前看是相同的。
示例 1:
输入: head = [1,2,3,3,2,1]
输出: true
示例 2:
输入: head = [1,2]
输出: false
提示:
• 链表 L 的长度范围为 [1, 105]
• 0 <= node.val <= 9
进阶:能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题?
思路1 使用stack来辅助 回文即正反看起来相同,第一种解法使用栈来压入所有元素,然后弹出栈元素同时遍历链表,看看二者每一个值是否一样。耗时224ms。
class Solution {
public:
bool isPalindrome ( ListNode * head ) {
ListNode * p = head ;
stack < int > temp_stack ;
while ( p != nullptr ) {
temp_stack . push ( p -> val );
p = p -> next ;
}
p = head ;
while ( ! temp_stack . empty ()) {
if ( p -> val != temp_stack . top ()) {
return false ;
}
p = p -> next ;
temp_stack . pop ();
}
return true ;
}
};
思路2 快慢指针找中点,翻转右侧链表,比较 快慢指针找中点,将慢指针置于中点或中点以左,快指针到末尾。翻转慢指针右侧节点,左侧子链表和右侧翻转过的两个链表进行比较,两链表的长度差值必须为1或0,相同位置元素必须相等。
class Solution {
public:
ListNode * reverseList ( ListNode * head ) {
ListNode * priv = nullptr ;
ListNode * p = head ;
while ( p != nullptr ) {
ListNode * nextTemp = p -> next ;
p -> next = priv ;
priv = p ;
p = nextTemp ;
}
return priv ;
}
bool isPalindrome ( ListNode * head ) {
if ( head -> next == nullptr ) {
return true ;
}
ListNode * slow = head ;
ListNode * fast = head ;
while ( fast != nullptr ) {
if ( fast -> next != nullptr && fast -> next -> next != nullptr ) {
fast = fast -> next -> next ;
} else {
break ;
}
slow = slow -> next ;
}
// slow为中点,slow下一个为头,fast做尾,翻转链表
ListNode * reverseHead = slow -> next ;
slow -> next = nullptr ;
ListNode * newSubList = reverseList ( reverseHead );
ListNode * p = head ;
ListNode * q = newSubList ;
while ( p != nullptr && q != nullptr ) {
if ( p -> val != q -> val ) {
return false ;
}
p = p -> next ;
q = q -> next ;
if ( p == nullptr && q != nullptr && q -> next != nullptr ) {
return false ;
}
if ( q == nullptr && p != nullptr && p -> next != nullptr ) {
return false ;
}
}
return true ;
}
};
思路3 将链表值复制到数组,双指针比较 class Solution {
public:
bool isPalindrome ( ListNode * head ) {
vector < int > vals ;
while ( head != nullptr ) {
vals . emplace_back ( head -> val );
head = head -> next ;
}
for ( int i = 0 , j = ( int ) vals . size () - 1 ; i < j ; ++ i , -- j ) {
if ( vals [ i ] != vals [ j ]) {
return false ;
}
}
return true ;
}
};
删除链表的倒数第 N 个结点 删除链表的倒数第 N 个结点
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。
示例 1:
输入:head = [1,2,3,4,5], n = 2
输出:[1,2,3,5]
示例 2
输入:head = [1], n = 1
输出:[]
示例 3:
输入:head = [1,2], n = 1
输出:[1]
提示:
链表中结点的数目为 sz
1 <= sz <= 30
0 <= Node.val <= 100
1 <= n <= sz
进阶:你能尝试使用一趟扫描实现吗?
思路1 首先特判长度为1的,直接返回空。如果长度大于1,使用map记录下下标和每个节点的地址,遍历一遍后,通过 count 长度,和 n 值,算出需要删除节点index的上一个节点的地址,注意如果删除的是第一个,直接返回 head->next .
class Solution {
public:
ListNode * removeNthFromEnd ( ListNode * head , int n ) {
if ( head -> next == nullptr )
return nullptr ;
ListNode * p = head ;
unordered_map < int , ListNode *> indexMap ;
int count = 0 ;
while ( p ) {
indexMap [ count ++ ] = p ;
p = p -> next ;
}
int index = count - n - 1 ;
if ( index < 0 ) {
return head -> next ;
}
indexMap [ index ] -> next = indexMap [ index ] -> next -> next ;
return head ;
}
};
官方题解 使用栈存储,弹出第n个就是需要删除的节点,此时再多弹出一个,就可以修改 next 指针来删除这个点。注意可以使用dummyHead哑节点,就不用对头节点特判了。
class Solution {
public:
ListNode * removeNthFromEnd ( ListNode * head , int n ) {
ListNode * dummy = new ListNode ( 0 , head );
stack < ListNode *> stk ;
ListNode * cur = dummy ;
while ( cur ) {
stk . push ( cur );
cur = cur -> next ;
}
// 弹出第n个,再弹出一个,就是需要删除的节点的上一个
for ( int i = 0 ; i < n ; ++ i ) {
stk . pop ();
}
// 将prev节点指向倒数第n个节点的下一个节点,即可实现删除
ListNode * prev = stk . top ();
prev -> next = prev -> next -> next ;
ListNode * ans = dummy -> next ;
delete dummy ;
return ans ;
}
};
链表表示的两数相加 链表表示的两数相加
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
即数字 `435` ,表示为链表: `5->3->4`
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:
输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
示例 2:
输入:l1 = [0], l2 = [0]
输出:[0]
示例 3:
输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出:[8,9,9,9,0,0,0,1]
提示:
每个链表中的节点数在范围 [1, 100] 内
0 <= Node.val <= 9
题目数据保证列表表示的数字不含前导零
思路1 从头到尾遍历,两个链表相同位置的数是处于同等位上的数据,使用小学数学加法计算进位即可。使用 / 取商,使用 % 取余。控制好进位,最后如果最高位相加的结果除10不为0,即仍然需要进位,则需要加一个节点。
class Solution {
public:
ListNode * addTwoNumbers ( ListNode * l1 , ListNode * l2 ) {
ListNode * newHead = new ListNode ( - 1 );
ListNode * q = newHead ;
int carry = 0 ;
while ( l1 || l2 ) {
int l1Value = l1 ? l1 -> val : 0 ;
int l2Value = l2 ? l2 -> val : 0 ;
int result = l1Value + l2Value + carry ;
int thisNodeValue = result % 10 ;
ListNode * thisNode = new ListNode ( thisNodeValue );
newHead -> next = thisNode ;
newHead = thisNode ;
carry = result / 10 ;
if ( l1 )
l1 = l1 -> next ;
if ( l2 )
l2 = l2 -> next ;
}
if ( carry > 0 ) {
newHead -> next = new ListNode ( carry );
}
return q -> next ;
}
};
这里刚刚编写的时候,在外面和循环里面都定义了一个int carry,二者命名相同没有报错,Java是会有报错的。后面需要注意这个特性。
删除排序链表中的重复元素 删除排序链表中的重复元素
给定一个已排序的链表的头 head , 删除所有重复的元素,使每个元素只出现一次 。返回 已排序的链表 。
示例 1:
输入:head = [1,1,2]
输出:[1,2]
示例 2:
输入:head = [1,1,2,3,3]
输出:[1,2,3]
提示:
链表中节点数目在范围 [0, 300] 内
-100 <= Node.val <= 100
题目数据保证链表已经按升序 排列
思路 使用快慢指针,快指针一直往前检索重复值的节点,慢指针从头节点开始做比较,二者相同时,删除快指针所指的节点,不同时,慢指针移到快指针所在位置,快指针继续往前一步。
class Solution {
public:
ListNode * deleteDuplicates ( ListNode * head ) {
if ( head == nullptr || head -> next == nullptr ) {
return head ;
}
ListNode * fast = head -> next ;
ListNode * slow = head ;
while ( fast ) {
while ( fast != nullptr && ( fast -> val == slow -> val )) {
ListNode * next = fast -> next ;
slow -> next = slow -> next -> next ;
fast = next ;
}
slow = fast ;
if ( fast )
fast = fast -> next ;
}
return head ;
}
};
官方题解优化复刻 不同于数组,刚刚编写时,总有一种感觉快慢指针咬的很紧,其实用不到快慢指针,本节点的next和本节点相同时,直接删除跳过即可。注意要防止遍历到最后一个节点时,调用current->next->val 报错的问题。
class Solution {
public:
ListNode * deleteDuplicates ( ListNode * head ) {
if ( head == nullptr || head -> next == nullptr ) {
return head ;
}
ListNode * current = head ;
while ( current -> next ) {
if ( current -> val == current -> next -> val ) {
current -> next = current -> next -> next ;
} else {
current = current -> next ;
}
}
return head ;
}
};
删除排序链表中的重复元素 II 删除排序链表中的重复元素 II
给定一个已排序的链表的头 head , 删除原始链表中所有重复数字的节点,只留下不同的数字 。返回 已排序的链表 。
示例 1:
输入:head = [1,2,3,3,4,4,5]
输出:[1,2,5]
示例 2:
输入:head = [1,1,1,2,3]
输出:[2,3]
提示:
链表中节点数目在范围 [0, 300] 内
-100 <= Node.val <= 100
题目数据保证链表已经按升序 排列
思路 这个变化的题和上一题在流程上类似,就是对比的值变成了这个节点的 next 和 next->next 。故也可以使用一个指针来判断,但是要注意元素从头开始就重复的情况,所以最好加虚拟头节点来辅助。
class Solution {
public:
ListNode * deleteDuplicates ( ListNode * head ) {
if ( ! head ) {
return head ;
}
ListNode * dummy = new ListNode ( 0 , head );
ListNode * cur = dummy ;
while ( cur -> next && cur -> next -> next ) {
if ( cur -> next -> val == cur -> next -> next -> val ) {
int x = cur -> next -> val ;
while ( cur -> next && cur -> next -> val == x ) {
cur -> next = cur -> next -> next ;
}
} else {
cur = cur -> next ;
}
}
return dummy -> next ;
}
};
旋转链表 旋转链表
给你一个链表的头节点 head ,旋转链表,将链表每个节点向右移动 k 个位置。
示例 1:
输入:head = [1,2,3,4,5], k = 2
输出:[4,5,1,2,3]
示例 2:
输入:head = [0,1,2], k = 4
输出:[2,0,1]
提示:
链表中节点的数目在范围 [0, 500] 内
-100 <= Node.val <= 100
0 <= k <= 2 * 10^ 9
思路1 成环再掐断 先连成环,再从指定的位置断开。
例如长度为4,k为2,就需要从第二个节点往后断开,第二个节点作为尾节点,第三个节点为头。
class Solution {
public:
ListNode * rotateRight ( ListNode * head , int k ) {
if ( head == nullptr || head -> next == nullptr ) {
return head ;
}
int count = 0 ;
ListNode * tail = head ;
while ( tail -> next != nullptr ) {
count ++ ;
tail = tail -> next ;
}
count ++ ;
// 需要掐断的第几个节点,从这里之后掐断
int breakPos = count > k ? count - k : count - ( k % count );
// 二者相等,直接原地返回
if ( breakPos == count ) {
return head ;
}
// 先成环再掐断
ListNode * p = head ;
tail -> next = head ;
ListNode * newHead = p -> next ;
// p在头节点,移动到要断的这个节点
for ( int i = 0 ; i < breakPos - 1 ; i ++ ) {
p = p -> next ;
newHead = p -> next ;
}
p -> next = nullptr ;
return newHead ;
}
};
官方代码 class Solution {
public:
ListNode * rotateRight ( ListNode * head , int k ) {
if ( k == 0 || head == nullptr || head -> next == nullptr ) {
return head ;
}
int n = 1 ;
ListNode * iter = head ;
while ( iter -> next != nullptr ) {
iter = iter -> next ;
n ++ ;
}
int add = n - k % n ;
if ( add == n ) {
return head ;
}
iter -> next = head ;
while ( add -- ) {
iter = iter -> next ;
}
ListNode * ret = iter -> next ;
iter -> next = nullptr ;
return ret ;
}
};
流程上一致,写法上更简洁精炼。
分隔链表 分隔链表
给你一个链表的头节点 head 和一个特定值 x ,请你对链表进行分隔,使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。
你应当 保留 两个分区中每个节点的初始相对位置。
示例 1:
输入:head = [1,4,3,2,5,2], x = 3
输出:[1,2,2,4,3,5]
示例 2:
输入:head = [2,1], x = 2
输出:[1,2]
提示:
链表中节点的数目在范围 [0, 200] 内
-100 <= Node.val <= 100
-200 <= x <= 200
思路1 使用快慢指针,快指针一直往前,负责需要前移的节点的拆除,慢指针永远指向小于这个值的最新节点,负责小节点的承接。最好加一个虚拟头节点,来防止第一个节点即属于大节点的情况。
class Solution {
public:
ListNode * partition ( ListNode * head , int x ) {
if ( ! head || ! head -> next )
return head ;
// 使用头结点方便操作
ListNode * pre_node = new ListNode ( - 1 ), * pre = pre_node , * curr = pre ;
pre_node -> next = head ;
// curr指向小于x的结点的前一个结点,pre指向小于值结点链的最后一个结点
while ( curr && curr -> next ) {
// 将后链的小于值的结点摘下尾插前链中
if ( curr -> next -> val < x ) {
ListNode * tem = curr -> next ;
curr -> next = tem -> next ;
tem -> next = pre -> next ;
pre -> next = tem ;
// 当pre == curr时同时向后移动两个指针
if ( curr == pre )
curr = curr -> next ;
pre = tem ;
} else
curr = curr -> next ;
}
return pre_node -> next ;
}
};
官方题解 直观来说我们只需维护两个链表 small 和 large 即可,small 链表按顺序存储所有小于 x 的节点,large 链表按顺序存储所有大于等于 x 的节点。遍历完原链表后,我们只要将 small 链表尾节点指向 large 链表的头节点即能完成对链表的分隔。
为了实现上述思路,我们设 smallHead 和 largeHead 分别为两个链表的哑节点,即它们的 next 指针指向链表的头节点,这样做的目的是为了更方便地处理头节点为空的边界条件。同时设 small 和 large 节点指向当前链表的末尾节点。开始时 smallHead=small,largeHead=large。随后,从前往后遍历链表,判断当前链表的节点值是否小于 x,如果小于就将 small 的 next 指针指向该节点,否则将 large 的 next 指针指向该节点。
遍历结束后,我们将 large 的 next 指针置空,这是因为当前节点复用的是原链表的节点,而其 next 指针可能指向一个小于 x 的节点,我们需要切断这个引用。同时将 small 的 next 指针指向 largeHead 的 next 指针指向的节点,即真正意义上的 large 链表的头节点。最后返回 smallHead 的 next 指针即为我们要求的答案。
class Solution {
public:
ListNode * partition ( ListNode * head , int x ) {
ListNode * small = new ListNode ( 0 );
ListNode * smallHead = small ;
ListNode * large = new ListNode ( 0 );
ListNode * largeHead = large ;
while ( head != nullptr ) {
if ( head -> val < x ) {
small -> next = head ;
small = small -> next ;
} else {
large -> next = head ;
large = large -> next ;
}
head = head -> next ;
}
large -> next = nullptr ;
small -> next = largeHead -> next ;
return smallHead -> next ;
}
};
LRU缓存 LRU缓存
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在,则变更其数据值 value ;如果不存在,则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
示例:
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
提示:
1 <= capacity <= 3000
0 <= key <= 10000
0 <= value <= 105
最多调用 2 * 105 次 get 和 put
思路1 刚拿到有点懵,对于更新、插入、容量判断感觉还可以摸索实现,就是长期未用还不知如何实现。看到这张图,感觉就比较清晰了。触发过的往上移,那第一个节点就是最久未使用的。
LRU 缓存机制可以通过哈希表辅以双向链表实现,我们用一个哈希表和一个双向链表维护所有在缓存中的键值对。
双向链表按照被使用的顺序存储了这些键值对,靠近头部的键值对是最近使用的,而靠近尾部的键值对是最久未使用的。
哈希表即为普通的哈希映射(HashMap),通过缓存数据的键映射到其在双向链表中的位置。
这样以来,我们首先使用哈希表进行定位,找出缓存项在双向链表中的位置,随后将其移动到双向链表的头部,即可在 O(1) 的时间内完成 get 或者 put 操作。具体的方法如下:
对于 get 操作,首先判断 key 是否存在:
如果 key 不存在,则返回 −1;
如果 key 存在,则 key 对应的节点是最近被使用的节点。通过哈希表定位到该节点在双向链表中的位置,并将其移动到双向链表的头部,最后返回该节点的值。
对于 put 操作,首先判断 key 是否存在:
如果 key 不存在,使用 key 和 value 创建一个新的节点,在双向链表的头部添加该节点,并将 key 和该节点添加进哈希表中。然后判断双向链表的节点数是否超出容量,如果超出容量,则删除双向链表的尾部节点,并删除哈希表中对应的项;
如果 key 存在,则与 get 操作类似,先通过哈希表定位,再将对应的节点的值更新为 value,并将该节点移到双向链表的头部。
上述各项操作中,访问哈希表的时间复杂度为 O(1),在双向链表的头部添加节点、在双向链表的尾部删除节点的复杂度也为 O(1)。而将一个节点移到双向链表的头部,可以分成「删除该节点」和「在双向链表的头部添加节点」两步操作,都可以在 O(1) 时间内完成。
小贴士
在双向链表的实现中,使用一个伪头部(dummy head)和伪尾部(dummy tail)标记界限,这样在添加节点和删除节点的时候就不需要检查相邻的节点是否存在。
根据官方思想复刻 struct DoubleLinkedNode
{
int key ;
int value ;
DoubleLinkedNode * next ;
DoubleLinkedNode * prev ;
DoubleLinkedNode ( int key , int value ) : key ( key ), value ( value ), next ( nullptr ), prev ( nullptr ) {}
DoubleLinkedNode () : key ( 0 ), value ( 0 ), next ( nullptr ), prev ( nullptr ) {}
};
class LRUCache
{
private:
// map 的key存储的是节点的key, value存放指向节点地址的指针
unordered_map < int , DoubleLinkedNode *> dataMap ;
DoubleLinkedNode * dummyHead = new DoubleLinkedNode ( 0 , 0 );
DoubleLinkedNode * dummytail = new DoubleLinkedNode ( 0 , 0 );
int tempSize = 0 ;
int capacity = 0 ;
public:
LRUCache ( int _capacity )
{
capacity = _capacity ;
dummyHead -> next = dummytail ;
dummytail -> prev = dummytail ;
}
int get ( int key )
{
if ( dataMap . count ( key ) > 0 )
{
// 将查询过的节点移动到头部
moveToHead ( dataMap [ key ]);
return dataMap [ key ] -> value ;
}
else
{
return - 1 ;
}
}
void put ( int key , int value )
{
// 判断存在性
if ( dataMap . count ( key ) > 0 )
{
// 修改节点的value值,移到最前
dataMap [ key ] -> value = value ;
moveToHead ( dataMap [ key ]);
}
else
{
// 新建节点
DoubleLinkedNode * newNode = new DoubleLinkedNode ( key , value );
// 添加进头部
addToHead ( newNode );
// 添加进数据集
dataMap [ newNode -> key ] = newNode ;
tempSize ++ ;
// 检查容量
if ( tempSize > capacity )
{
removeTailNode ();
tempSize -- ;
}
}
}
void moveToHead ( DoubleLinkedNode * node )
{
removeNode ( node );
addToHead ( node );
}
void addToHead ( DoubleLinkedNode * node )
{
node -> next = dummyHead -> next ;
node -> prev = dummyHead ;
dummyHead -> next -> prev = node ;
dummyHead -> next = node ;
}
void removeNode ( DoubleLinkedNode * node )
{
node -> next -> prev = node -> prev ;
node -> prev -> next = node -> next ;
node -> next = nullptr ;
node -> prev = nullptr ;
}
void removeTailNode ()
{
DoubleLinkedNode * tail = dummytail -> prev ;
// 删除数据集中的内容
dataMap . erase ( tail -> key );
removeNode ( tail );
delete tail ;
}
};
官方版本如下,在超出容量移除的时候,写法略有不同。
struct DLinkedNode {
int key , value ;
DLinkedNode * prev ;
DLinkedNode * next ;
DLinkedNode () : key ( 0 ), value ( 0 ), prev ( nullptr ), next ( nullptr ) {}
DLinkedNode ( int _key , int _value ) : key ( _key ), value ( _value ), prev ( nullptr ), next ( nullptr ) {}
};
class LRUCache {
private:
unordered_map < int , DLinkedNode *> cache ;
DLinkedNode * head ;
DLinkedNode * tail ;
int size ;
int capacity ;
public:
LRUCache ( int _capacity ) : capacity ( _capacity ), size ( 0 ) {
// 使用伪头部和伪尾部节点
head = new DLinkedNode ();
tail = new DLinkedNode ();
head -> next = tail ;
tail -> prev = head ;
}
int get ( int key ) {
if ( ! cache . count ( key )) {
return - 1 ;
}
// 如果 key 存在,先通过哈希表定位,再移到头部
DLinkedNode * node = cache [ key ];
moveToHead ( node );
return node -> value ;
}
void put ( int key , int value ) {
if ( ! cache . count ( key )) {
// 如果 key 不存在,创建一个新的节点
DLinkedNode * node = new DLinkedNode ( key , value );
// 添加进哈希表
cache [ key ] = node ;
// 添加至双向链表的头部
addToHead ( node );
++ size ;
if ( size > capacity ) {
// 如果超出容量,删除双向链表的尾部节点
DLinkedNode * removed = removeTail ();
// 删除哈希表中对应的项
cache . erase ( removed -> key );
// 防止内存泄漏
delete removed ;
-- size ;
}
}
else {
// 如果 key 存在,先通过哈希表定位,再修改 value,并移到头部
DLinkedNode * node = cache [ key ];
node -> value = value ;
moveToHead ( node );
}
}
void addToHead ( DLinkedNode * node ) {
node -> prev = head ;
node -> next = head -> next ;
head -> next -> prev = node ;
head -> next = node ;
}
void removeNode ( DLinkedNode * node ) {
node -> prev -> next = node -> next ;
node -> next -> prev = node -> prev ;
}
void moveToHead ( DLinkedNode * node ) {
removeNode ( node );
addToHead ( node );
}
DLinkedNode * removeTail () {
DLinkedNode * node = tail -> prev ;
removeNode ( node );
return node ;
}
};
双链表对比单链表更不容易写断,可以先拆出来,再添加进去。将两边的同时要注意两个指针需要更新,next和prev两个都需要仔细操作;
拆分时将此节点的左右两个节点二指针互相连接即可。
添加时,需要将待添加位置的左右两个节点都指向这个节点,这个节点的next和prev也要指向插入位置左右的两个节点。
思路上很简单,更加考验代码细节设计编写。
C++ 提供了多种数据结构,每种都有其特定的用途和优势。以下是常见的 C++ 数据结构及其简单示例:
数组 (Array) 最基本的线性数据结构,元素在内存中连续存储。
#include <iostream>
using namespace std ;
int main () {
int arr [ 5 ] = { 1 , 2 , 3 , 4 , 5 };
for ( int i = 0 ; i < 5 ; i ++ ) {
cout << arr [ i ] << " " ;
}
return 0 ;
}
向量 (Vector) 动态数组,可以自动调整大小。
#include <iostream>
#include <vector>
using namespace std ;
int main () {
vector < int > vec = { 1 , 2 , 3 };
vec . push_back ( 4 ); // 添加元素
vec . pop_back (); // 移除最后一个元素
for ( int num : vec ) {
cout << num << " " ;
}
return 0 ;
}
链表 (Linked List) 包括单向链表、双向链表和循环链表。
#include <iostream>
using namespace std ;
struct Node {
int data ;
Node * next ;
};
int main () {
Node * head = new Node { 1 , nullptr };
head -> next = new Node { 2 , nullptr };
head -> next -> next = new Node { 3 , nullptr };
Node * current = head ;
while ( current != nullptr ) {
cout << current -> data << " " ;
current = current -> next ;
}
return 0 ;
}
栈 (Stack) 后进先出(LIFO)的数据结构。
#include <iostream>
#include <stack>
using namespace std ;
int main () {
stack < int > s ;
s . push ( 1 );
s . push ( 2 );
s . push ( 3 );
while ( ! s . empty ()) {
cout << s . top () << " " ;
s . pop ();
}
return 0 ;
}
除了pop,push,empty,top之外,还有size()用于查看元素个数,swap用于置换两个栈道内容。
swap() • 功能:交换两个栈的内容。 • 示例代码:
#include <vector>
#include <iostream>
#include <stack>
using namespace std ;
int main () {
stack < int > stack1 ;
stack1 . push ( 10 );
stack1 . push ( 20 );
stack < int > stack2 ;
stack2 . push ( 30 );
stack2 . push ( 40 );
stack1 . swap ( stack2 );
// 输出交换后 stack1 的栈顶元素
cout << "交换后 stack1 的栈顶元素: " << stack1 . top () << endl ;
return 0 ;
}
队列 (Queue) 先进先出(FIFO)的数据结构。
#include <iostream>
#include <queue>
using namespace std ;
int main () {
queue < int > q ;
q . push ( 1 );
q . push ( 2 );
q . push ( 3 );
while ( ! q . empty ()) {
cout << q . front () << " " ;
q . pop ();
}
return 0 ;
}
优先队列 (Priority Queue) 元素按优先级出队。
#include <iostream>
#include <queue>
using namespace std ;
int main () {
priority_queue < int > pq ;
pq . push ( 3 );
pq . push ( 1 );
pq . push ( 4 );
pq . push ( 2 );
while ( ! pq . empty ()) {
cout << pq . top () << " " ;
pq . pop ();
}
return 0 ;
}
队列有front,back,empty,push,pop,size等常用函数。
集合 (Set) 存储唯一元素的有序集合,基于红黑树,可以自动排序,且元素唯一。重复添加相同元素,只有第一个可以成功添加。 常用方法有:insert,erase, clear, find寻找元素;count返回集合元素数量(0或1),
find() • 功能:查找指定元素,若找到则返回指向该元素的迭代器,未找到则返回 end() 迭代器。 • 实例代码:
#include <set>
#include <iostream>
int main () {
std :: set < int > intSet = { 3 , 7 , 10 , 15 };
auto it = intSet . find ( 7 );
if ( it != intSet . end ()) {
std :: cout << "找到元素: " << * it << std :: endl ;
} else {
std :: cout << "未找到元素" << std :: endl ;
}
return 0 ;
}
#include <iostream>
#include <set>
using namespace std ;
int main () {
set < int > s = { 3 , 1 , 4 , 1 , 5 , 9 };
for ( int num : s ) {
cout << num << " " ;
}
return 0 ;
}
映射 (Map) 键值对集合。
#include <iostream>
#include <map>
using namespace std ;
int main () {
map < string , int > ages ;
ages [ "Alice" ] = 25 ;
ages [ "Bob" ] = 30 ;
for ( const auto & pair : ages ) {
cout << pair . first << ": " << pair . second << endl ;
}
return 0 ;
}
哈希表 (Unordered Map) 基于哈希表的键值对集合。
#include <iostream>
#include <unordered_map>
using namespace std ;
int main () {
unordered_map < string , int > ages ;
ages [ "Alice" ] = 25 ;
ages [ "Bob" ] = 30 ;
for ( const auto & pair : ages ) {
cout << pair . first << ": " << pair . second << endl ;
}
return 0 ;
}
树 (Tree) 包括二叉树、二叉搜索树、AVL树等。
#include <iostream>
using namespace std ;
struct TreeNode {
int val ;
TreeNode * left ;
TreeNode * right ;
TreeNode ( int x ) : val ( x ), left ( nullptr ), right ( nullptr ) {}
};
void inorder ( TreeNode * root ) {
if ( root == nullptr ) return ;
inorder ( root -> left );
cout << root -> val << " " ;
inorder ( root -> right );
}
int main () {
TreeNode * root = new TreeNode ( 1 );
root -> left = new TreeNode ( 2 );
root -> right = new TreeNode ( 3 );
inorder ( root );
return 0 ;
}
图 (Graph) 可以使用邻接表或邻接矩阵表示。
#include <iostream>
#include <vector>
using namespace std ;
class Graph {
int V ;
vector < vector < int >> adj ;
public:
Graph ( int V ) : V ( V ), adj ( V ) {}
void addEdge ( int u , int v ) {
adj [ u ]. push_back ( v );
adj [ v ]. push_back ( u ); // 无向图
}
void print () {
for ( int i = 0 ; i < V ; i ++ ) {
cout << "顶点 " << i << " 的邻居: " ;
for ( int neighbor : adj [ i ]) {
cout << neighbor << " " ;
}
cout << endl ;
}
}
};
int main () {
Graph g ( 4 );
g . addEdge ( 0 , 1 );
g . addEdge ( 0 , 2 );
g . addEdge ( 1 , 3 );
g . print ();
return 0 ;
}
堆 (Heap) 用于实现优先队列的完全二叉树。
#include <iostream>
#include <queue>
using namespace std ;
int main () {
// 最大堆
priority_queue < int > max_heap ;
// 最小堆
priority_queue < int , vector < int > , greater < int >> min_heap ;
max_heap . push ( 3 );
max_heap . push ( 1 );
max_heap . push ( 4 );
cout << "最大堆: " ;
while ( ! max_heap . empty ()) {
cout << max_heap . top () << " " ;
max_heap . pop ();
}
min_heap . push ( 3 );
min_heap . push ( 1 );
min_heap . push ( 4 );
cout << " \n 最小堆: " ;
while ( ! min_heap . empty ()) {
cout << min_heap . top () << " " ;
min_heap . pop ();
}
return 0 ;
}
另外还有unordere*系列的容器,摈弃了自动排序,在时间复杂度上有了提升,像 unordered_map 等。
还有multi系列,让一些不可重复存储的容器,比如map和set,支持重复存储相同元素,就可以顺带使用其排序功能,快速实现一些功能。
这些数据结构是C++编程中常用的基础,STL(标准模板库)为许多数据结构提供了现成的实现,但在某些情况下,了解如何手动实现这些数据结构也是非常重要的。
八大数据结构 数组 数组是一种线性表数据结构,它使用一组连续的内存空间,来存储一组具有相同类型的数据。
C++举例:
#include <iostream>
int main () {
// 定义一个整型数组,大小为5
int arr [ 5 ] = { 1 , 2 , 3 , 4 , 5 };
// 访问数组元素
std :: cout << "第一个元素: " << arr [ 0 ] << std :: endl ;
std :: cout << "第二个元素: " << arr [ 1 ] << std :: endl ;
// 修改数组元素
arr [ 2 ] = 10 ;
std :: cout << "修改后的第三个元素: " << arr [ 2 ] << std :: endl ;
return 0 ;
}
数组的优点
随机访问:由于数组在内存中是连续存储的,因此可以通过索引快速访问任何元素,时间复杂度为O(1)。 缓存友好:连续的内存空间使得数组在缓存中更容易被加载和访问,提高了访问效率。 简单易用:数组的定义和使用非常简单,易于理解和实现。 数组的缺点
大小固定:数组的大小在定义时就确定了,无法动态扩展或缩小。如果需要存储更多的元素,就需要重新定义一个更大的数组,并将原数组的元素复制到新数组中。 插入和删除效率低:在数组中插入或删除元素时,需要移动大量的元素,时间复杂度为O(n)。 内存浪费:如果数组的大小定义得过大,可能会导致内存浪费;如果定义得过小,可能会导致数据溢出。 数组是一种简单而高效的数据结构,适用于需要快速随机访问元素的场景。然而,由于其 大小固定和插入删除效率低 的缺点,在需要动态调整大小或频繁插入删除元素的场景中,可能需要使用其他数据结构,如 链表 、 动态数组 (如C++中的std::vector)等。
动态数组原理 在C++中,动态数组的实现是基于其 内存管理机制 的,刚刚写到的静态数组由于其大小固定,使用上有诸多不便。
动态数组的实现原理是通过 内存分配 和 内存释放 来实现的。当需要添加元素时,如果当前数组已满,就需要重新分配一块更大的内存空间,并 将原数组的元素复制到新数组 中。当需要删除元素时,如果当前数组的元素较少,就需要释放内存空间,并将原数组的元素复制到新数组中。
动态数组的实现方式有很多种,其中最常见的是使用 指针 和 内存分配函数 来实现。在C++中,可以使用 new 运算符来分配内存,使用 delete 运算符来释放内存。
#include <iostream>
int main () {
// 定义一个动态数组,初始大小为5
int * arr = new int [ 5 ];
// 向数组中添加元素
arr [ 0 ] = 1 ;
arr [ 1 ] = 2 ;
arr [ 2 ] = 3 ;
arr [ 3 ] = 4 ;
arr [ 4 ] = 5 ;
// 输出数组元素
for ( int i = 0 ; i < 5 ; i ++ ) {
std :: cout << arr [ i ] << " " ;
}
std :: cout << std :: endl ;
// 重新分配内存,大小为10
int * newArr = new int [ 10 ];
// 将原数组的元素复制到新数组中
for ( int i = 0 ; i < 5 ; i ++ ) {
newArr [ i ] = arr [ i ];
}
// 释放原数组的内存
delete [] arr ;
// 将旧的数组指针指向新申请的大数组
arr = newArr ;
// 向数组中添加元素
arr [ 5 ] = 6 ;
arr [ 6 ] = 7 ;
arr [ 7 ] = 8 ;
arr [ 8 ] = 9 ;
arr [ 9 ] = 10 ;
// 输出数组元素
for ( int i = 0 ; i < 10 ; i ++ ) {
std :: cout << arr [ i ] << " " ;
}
std :: cout << std :: endl ;
// 释放新数组的内存
delete [] newArr ;
return 0 ;
}
链表 链表是一种非连续存储的线性结构,每个元素包含 数据 和指向下一个元素的指针 。链表的优点是插入和删除操作高效 ,但访问速度较慢 。
单向链表每个节点包含数据和指向下一个节点的指针。双向链表每个节点包含数据和 指向前一个节点和后一个节点 的指针。
#include <iostream>
// 定义链表节点
struct ListNode {
int val ;
ListNode * next ;
ListNode ( int x ) : val ( x ), next ( NULL ) {}
};
int main () {
// 创建链表
ListNode * head = new ListNode ( 1 );
ListNode * second = new ListNode ( 2 );
ListNode * third = new ListNode ( 3 );
head -> next = second ;
second -> next = third ;
// 访问链表元素
ListNode * current = head ;
while ( current != NULL ) {
std :: cout << current -> val << " " ;
current = current -> next ;
}
return 0 ;
}
链表的优点
动态大小:链表的大小可以动态增长或缩小,不需要预先分配固定大小的内存。 插入和删除高效:在链表中插入或删除元素时,只需要修改指针,不需要移动大量的元素,时间复杂度为O(1)。 链表的缺点
随机访问效率低:由于链表的元素不是连续存储的,因此无法通过索引快速访问元素,需要从头开始遍历链表,时间复杂度为O(n)。 额外的内存开销:链表的每个节点需要额外的指针来指向下一个节点,增加了内存开销。 链表是一种灵活的数据结构,适用于需要 频繁插入和删除元素 的场景。然而,由于其随机访问效率低的缺点,在需要快速随机访问元素的场景中,可能需要使用其他数据结构,如数组、动态数组(如C++中的std::vector)等。
栈 栈(Stack)是一种后进先出(LIFO, Last In First Out)的数据结构,它只允许在一端进行插入和删除操作。这一端通常被称为栈顶。栈的操作主要有两种:压入(push)和弹出(pop)。压入操作将元素添加到栈顶,弹出操作则从栈顶移除元素。
#include <iostream>
#include <stack>
int main () {
// 创建一个栈
std :: stack < int > myStack ;
// 压入元素
myStack . push ( 1 );
myStack . push ( 2 );
myStack . push ( 3 );
// 访问栈顶元素
std :: cout << "栈顶元素: " << myStack . top () << std :: endl ;
// 弹出栈顶元素
myStack . pop ();
// 再次访问栈顶元素
std :: cout << "弹出一个元素后,栈顶元素: " << myStack . top () << std :: endl ;
return 0 ;
}
栈的优点
简单高效:栈的操作非常简单,只需要在栈顶进行插入和删除操作,时间复杂度为O(1)。 内存管理方便:栈的内存管理由系统自动完成,不需要手动分配和释放内存。 支持递归:栈在递归算法中非常有用,因为递归调用的返回地址和局部变量都存储在栈中。 栈的缺点
大小固定:栈的大小通常是固定的,如果栈满了,再进行压入操作就会导致栈溢出。 不支持随机访问:栈不支持随机访问,只能访问栈顶元素。 栈是一种简单而高效的数据结构,适用于需要 后进先出 操作的场景,如函数调用、表达式求值等。然而,由于其 大小固定和不支持随机访问 ,在需要动态调整大小或随机访问元素的场景中,可能需要如动态数组(如C++中的std::vector)等的数据结构。
队列 队列(Queue)是一种先进先出(FIFO, First In First Out)的数据结构,它只允许在一端进行插入操作(队尾),在另一端进行删除操作(队头)。队列常用于广度优先搜索和任务调度等场景。
#include <iostream>
#include <queue>
int main () {
// 创建一个队列
std :: queue < int > myQueue ;
// 入队操作
myQueue . push ( 1 );
myQueue . push ( 2 );
myQueue . push ( 3 );
// 访问队头元素
std :: cout << "队头元素: " << myQueue . front () << std :: endl ;
// 出队操作
myQueue . pop ();
// 再次访问队头元素
std :: cout << "出队一个元素后,队头元素: " << myQueue . front () << std :: endl ;
return 0 ;
}
队列的优点
简单高效:队列的操作非常简单,只需要在队尾进行插入操作,在队头进行删除操作,时间复杂度为O(1)。 顺序性:队列能够保持元素的顺序,先进入队列的元素先被处理,这对于需要按照顺序处理数据的场景非常有用。 支持并发:在多线程环境中,队列可以用于实现线程安全的数据共享,例如生产者-消费者模型。 队列的缺点
大小固定:队列的大小通常是固定的,如果队列满了,再进行插入操作就会导致队列溢出。 不支持随机访问:队列不支持随机访问,只能访问队头和队尾的元素。 树 树(Tree)是一种非线性的数据结构,它由 节点(Node)和边(Edge) 组成。每个节点可以有 零个或多个 子节点,而每个子节点又可以有零个或多个子节点,以此类推。树的顶部节点称为根节点(Root),没有子节点的节点称为叶子节点(Leaf)。树结构常用于表示 层次关系 的数据,如文件系统。
二叉树(Binary Tree) 是一种特殊的树结构,它的每个节点 最多有两个 子节点,通常称为左子节点和右子节点。
二叉树的特点
每个节点最多有两个子节点:这是二叉树的定义,也是它与其他树结构的主要区别。 子节点的顺序:左子节点和右子节点是有顺序的,不能随意交换。即二叉树是有序树 递归定义:二叉树可以递归地定义为一个节点,该节点有一个数据元素和两个指向子二叉树的指针。 二叉树的类型
满二叉树:除了叶子节点外, 每个节点都有两个子节点 ,并且所有叶子节点都在同一层。 完全二叉树:除了最后一层外,其他层的节点数都是满的,并且最后一层的节点都靠左排列。 平衡二叉树:树上的每个节点,其左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
二叉树的遍历
前序遍历:先访问根节点,然后递归遍历左子树,最后递归遍历右子树。 中序遍历:先递归遍历左子树,然后访问根节点,最后递归遍历右子树。 后序遍历:先递归遍历左子树,然后递归遍历右子树,最后访问根节点。 层序遍历:从根节点开始,按照从上到下、从左到右的顺序依次访问每个节点。 前三种称为深度优先遍历(DFS),层序遍历为广度优先遍历(BFS)。
#include <iostream>
// 定义二叉树节点
struct TreeNode {
int val ;
TreeNode * left ;
TreeNode * right ;
TreeNode ( int x ) : val ( x ), left ( NULL ), right ( NULL ) {}
};
// 前序遍历
void preorderTraversal ( TreeNode * root ) {
if ( root == NULL ) return ;
std :: cout << root -> val << " " ;
preorderTraversal ( root -> left );
preorderTraversal ( root -> right );
}
// 中序遍历
void inorderTraversal ( TreeNode * root ) {
if ( root == NULL ) return ;
inorderTraversal ( root -> left );
std :: cout << root -> val << " " ;
inorderTraversal ( root -> right );
}
// 后序遍历
void postorderTraversal ( TreeNode * root ) {
if ( root == NULL ) return ;
postorderTraversal ( root -> left );
postorderTraversal ( root -> right );
std :: cout << root -> val << " " ;
}
// 层序遍历
void levelOrderTraversal ( TreeNode * root ) {
if ( root == NULL ) return ;
std :: queue < TreeNode *> q ;
q . push ( root );
while ( ! q . empty ()) {
TreeNode * node = q . front ();
q . pop ();
std :: cout << node -> val << " " ;
if ( node -> left != NULL ) q . push ( node -> left );
if ( node -> right != NULL ) q . push ( node -> right );
}
}
int main () {
// 创建二叉树
TreeNode * root = new TreeNode ( 1 );
root -> left = new TreeNode ( 2 );
root -> right = new TreeNode ( 3 );
root -> left -> left = new TreeNode ( 4 );
root -> left -> right = new TreeNode ( 5 );
// 前序遍历二叉树
std :: cout << "前序遍历结果: " ;
preorderTraversal ( root );
std :: cout << std :: endl ;
// 中序遍历二叉树
std :: cout << "中序遍历结果: " ;
inorderTraversal ( root );
std :: cout << std :: endl ;
// 后序遍历二叉树
std :: cout << "后序遍历结果: " ;
postorderTraversal ( root );
std :: cout << std :: endl ;
// 层序遍历二叉树
std :: cout << "层序遍历结果: " ;
levelOrderTraversal ( root );
std :: cout << std :: endl ;
return 0 ;
}
树的优点
层次结构清晰:树结构能够清晰地表示数据之间的层次关系,例如文件系统、组织结构等。 高效的搜索和插入操作:对于平衡树(如二叉搜索树),搜索、插入和删除操作的平均时间复杂度为O(log n),其中n是树中节点的数量。 动态数据结构:树的大小可以动态增长或缩小,不需要预先分配固定大小的内存。 树的缺点
实现复杂:相比于线性数据结构(如数组、链表),树的实现通常更加复杂,需要更多的代码和逻辑。 空间开销较大:树的每个节点需要额外的指针来指向其子节点,这增加了内存开销。 不支持随机访问:树不支持像数组那样的随机访问,访问特定节点需要从根节点开始遍历。 树是一种非常有用的数据结构,适用于表示 层次关系和需要高效搜索、插入操作 的场景。然而,由于其 实现复杂和空间开销较大 的缺点,在简单的线性数据结构能够满足需求的情况下,可能不需要使用树。
哈希表 哈希表(Hash Table)是一种根据关键码值(Key value)而直接进行访问的数据结构。它通过哈希函数 将键映射到数组 中的位置,从而实现快速查找。。这个映射函数叫做哈希函数,存放记录的数组叫做哈希表。哈希表的优点是查找速度快,但需要处理哈希冲突。
#include <iostream>
#include <unordered_map>
#include <string>
int main () {
// 创建一个哈希表
std :: unordered_map < std :: string , int > hashTable ;
// 插入键值对
hashTable [ "apple" ] = 1 ;
hashTable [ "banana" ] = 2 ;
hashTable [ "cherry" ] = 3 ;
// 查找键值对
std :: cout << "The value of 'apple' is: " << hashTable [ "apple" ] << std :: endl ;
// 删除键值对
hashTable . erase ( "banana" );
// 遍历哈希表
for ( const auto & pair : hashTable ) {
std :: cout << pair . first << ": " << pair . second << std :: endl ;
}
return 0 ;
}
哈希表的优点
快速查找:哈希表的查找、插入和删除操作的平均时间复杂度为O(1),这使得它在处理大量数据时非常高效。 灵活性:哈希表可以存储不同类型的数据,并且可以动态调整大小以适应数据的增长或减少。 高效的内存使用:哈希表通常比其他数据结构(如树)更节省内存,因为它们不需要维护复杂的指针结构。 哈希表的缺点
哈希冲突:不同的关键码值可能映射到相同的哈希表位置,这称为哈希冲突。解决哈希冲突需要额外的处理,这可能会增加时间和空间复杂度。 不支持顺序访问:哈希表不支持像数组或链表那样的顺序访问,因此在需要按顺序遍历数据的场景中可能不太适用。 哈希函数的选择:哈希表的性能很大程度上取决于哈希函数的选择。一个好的哈希函数应该能够均匀地分布关键码值,以减少哈希冲突的可能性。 哈希表是一种非常有用的数据结构,适用于需要快速查找和插入操作的场景。然而,由于其 哈希冲突和灵活性,不保证顺序 的缺点,在需要 顺序访问 或需要 维护复杂指针结构 的场景中,可能需要使用其他数据结构,如树或数组等。
堆 堆(Heap)是一种特殊的树结构,通常是一个 完全二叉树 。堆分为最大堆和最小堆,其中最大堆的每个节点的值都大于或等于其子节点的值,最小堆的每个节点的值都小于或等于其子节点的值。堆常用于实现优先队列,其中最大堆用于实现最大优先队列,最小堆用于实现最小优先队列。
#include <iostream>
#include <queue>
int main () {
// 创建一个最大堆
std :: priority_queue < int > maxHeap ;
// 插入元素
maxHeap . push ( 3 );
maxHeap . push ( 1 );
maxHeap . push ( 4 );
maxHeap . push ( 1 );
maxHeap . push ( 5 );
// 访问最大元素
std :: cout << "最大元素: " << maxHeap . top () << std :: endl ;
// 删除最大元素
maxHeap . pop ();
// 再次访问最大元素
std :: cout << "删除最大元素后,最大元素: " << maxHeap . top () << std :: endl ;
return 0 ;
}
堆的优点
高效的插入和删除操作:在堆中插入和删除元素的时间复杂度为O(log n),其中n是堆中元素的数量。这使得堆在处理大量数据时非常高效。 快速访问最大或最小元素:在最大堆中,根节点始终是最大元素;在最小堆中,根节点始终是最小元素。因此,可以在O(1)时间内访问最大或最小元素。 动态调整大小:堆可以动态调整大小,以适应数据的增长或减少。 堆的缺点
不支持随机访问:堆不支持像数组那样的随机访问,因此在需要按顺序遍历数据的场景中可能不太适用。 不保证元素的顺序:堆只保证根节点是最大或最小元素,而不保证其他元素的顺序。 空间开销:堆的每个节点需要额外的空间来存储其子节点的指针,这增加了内存开销。 堆是一种非常有用的数据结构,适用于需要快速访问最大或最小元素的场景,如优先队列。然而,由于其不支持随机访问和不保证元素顺序的特点,在某些特定场景下可能需要考虑其他数据结构。
图 图(Graph)是一种非线性的数据结构,由顶点(Vertex)和边(Edge)组成。顶点表示对象,边表示对象之间的关系。图分为有向图和无向图。图可以用来表示各种复杂的关系,如社交网络、交通网络、计算机网络等。
#include <iostream>
#include <vector>
#include <list>
class Graph {
private:
int numVertices ;
std :: vector < std :: list < int >> adjLists ;
public:
Graph ( int vertices ) : numVertices ( vertices ) {
adjLists . resize ( numVertices );
}
void addEdge ( int src , int dest ) {
adjLists [ src ]. push_back ( dest );
// 如果是无向图,需要添加反向边
// adjLists[dest].push_back(src);
}
void printGraph () {
for ( int i = 0 ; i < numVertices ; ++ i ) {
std :: cout << "Vertex " << i << ": " ;
for ( int neighbor : adjLists [ i ]) {
std :: cout << neighbor << " " ;
}
std :: cout << std :: endl ;
}
}
};
int main () {
Graph g ( 5 );
g . addEdge ( 0 , 1 );
g . addEdge ( 0 , 4 );
g . addEdge ( 1 , 2 );
g . addEdge ( 1 , 3 );
g . addEdge ( 1 , 4 );
g . addEdge ( 2 , 3 );
g . addEdge ( 3 , 4 );
g . printGraph ();
return 0 ;
}
图的优点
强大的表示能力:图可以表示各种复杂的关系,如社交网络中的朋友关系、交通网络中的道路连接等。 灵活性:图可以是有向的(边有方向)或无向的(边无方向),可以是加权的(边有权重)或无权的(边无权重)。 广泛的应用领域:图在许多领域都有广泛的应用,如计算机科学、数学、物理学、生物学、社会学等。 图的缺点
实现复杂:图的实现通常比其他数据结构更复杂,需要更多的代码和逻辑。 空间开销大:图的存储通常需要更多的空间,尤其是在处理大规模图时。 算法复杂度高:许多图算法的时间复杂度较高,如最短路径算法、最小生成树算法等。 图是一种非常强大的数据结构,适用于表示各种复杂的关系。然而,由于其实现复杂和空间开销大的缺点,在处理小规模数据或简单关系时,可能不需要使用图。
算法 算法思想 递归 递归是一种解决问题的方法,它将问题分解为更小的子问题,直到问题足够简单可以直接解决。递归的基本思想是将一个大问题分解为一个或多个相似的子问题,然后通过解决这些子问题来解决原始问题。
递归的基本步骤如下:
定义基本情况:确定递归的终止条件,即当问题足够简单时,不需要再分解为子问题,直接解决。 分解问题:将原始问题分解为一个或多个相似的子问题。 解决子问题:递归地解决子问题,得到子问题的解。 合并子问题:将子问题的解合并为原始问题的解。 #include <iostream>
int factorial ( int n ) {
if ( n == 0 ) {
return 1 ;
} else {
return n * factorial ( n - 1 );
}
}
int main () {
int n = 5 ;
int result = factorial ( n );
std :: cout << "Factorial of " << n << " is " << result << std :: endl ;
return 0 ;
}
递归的优点
简洁性:递归可以使代码更加简洁,因为它可以将复杂的问题分解为简单的子问题。 可扩展性:递归可以使算法更易于扩展,因为它可以将问题分解为更小的子问题,从而更容易地解决更大的问题。 递归的缺点
效率较低:递归的实现通常比迭代的实现效率较低,因为递归需要保存函数调用的状态,并且可能会导致栈溢出。 可读性较差:递归的实现可能会使代码变得难以理解,特别是当递归深度较大时。 递归是一种强大的算法思想,适用于解决许多问题。然而,递归的实现可能会导致效率较低,并且代码变得难以理解。在选择使用递归时,需要权衡其优点和缺点,并根据具体情况进行选择。
回溯 回溯是一种通过尝试不同的可能来解决问题的算法思想。它通常用于解决组合优化问题,如旅行商问题、子集和问题等。回溯的基本思想是从一个初始状态开始,尝试所有可能的选择,直到找到一个解或确定问题无解。
回溯的基本步骤如下:
定义初始状态:确定问题的初始状态,即问题的初始状态。 定义选择列表:确定在当前状态下可以进行的选择列表。 尝试选择:对于每个选择,尝试将其应用于当前状态,得到一个新的状态。 检查是否满足条件:检查新状态是否满足问题的条件,如果满足条件,则找到了一个解。 回溯:如果新状态不满足条件,则需要回溯到上一个状态,并尝试其他选择。 #include <iostream>
#include <vector>
void backtrack ( std :: vector < int >& nums , std :: vector < int >& path , std :: vector < std :: vector < int >>& result ) {
if ( path . size () == nums . size ()) {
result . push_back ( path );
return ;
}
for ( int num : nums ) {
if ( std :: find ( path . begin (), path . end (), num ) == path . end ()) {
path . push_back ( num );
backtrack ( nums , path , result );
path . pop_back ();
}
}
}
int main () {
std :: vector < int > nums = { 1 , 2 , 3 };
std :: vector < int > path ;
std :: vector < std :: vector < int >> result ;
backtrack ( nums , path , result );
for ( const auto & permutation : result ) {
for ( int num : permutation ) {
std :: cout << num << " " ;
}
std :: cout << std :: endl ;
}
return 0 ;
}
回溯的优点
灵活性:回溯可以使算法更灵活,因为它可以处理各种不同的问题。 易于理解:回溯的实现通常比其他算法更易于理解,因为它可以将问题分解为更小的子问题。 回溯的缺点
效率较低:回溯的实现通常比其他算法效率较低,因为它需要尝试所有可能的选择。 可读性较差:回溯的实现可能会使代码变得难以理解,特别是当递归深度较大时。 回溯是一种强大的算法思想,适用于解决组合优化问题。然而,回溯的实现可能会导致效率较低,并且代码变得难以理解。在选择使用回溯时,需要权衡其优点和缺点,并根据具体情况进行选择。
深度广度优先 深度优先搜索(DFS)和广度优先搜索(BFS)是两种常见的图遍历算法,用于在图中搜索特定的节点或路径。 深度优先搜索(DFS)是一种沿着树的深度遍历树的节点,尽可能深的搜索树的分支。它从根节点开始,沿着一条路径尽可能深入地搜索,直到无法继续为止,然后回溯到上一个节点,继续搜索其他路径。 广度优先搜索(BFS)是一种沿着树的宽度遍历树的节点。它从根节点开始,沿着树的宽度遍历节点,直到所有节点都被访问为止。
深度优先搜索(DFS)的基本步骤如下:
从起始节点开始,将其标记为已访问。 访问起始节点的所有未访问邻居节点,并将它们标记为已访问。 对于每个已访问的邻居节点,重复步骤2和3,直到所有节点都被访问。 广度优先搜索(BFS)的基本步骤如下:
从起始节点开始,将其标记为已访问,并将其加入队列。 从队列中取出一个节点,并访问它的所有未访问邻居节点,并将它们标记为已访问,并将它们加入队列。 重复步骤2和3,直到队列为空。 #include <iostream>
#include <vector>
#include <queue>
// 定义图的邻接表表示
std :: vector < std :: vector < int >> graph = {
{ 1 , 2 }, // 节点0的邻居节点为1和2
{ 0 , 2 , 3 }, // 节点1的邻居节点为0、2和3
{ 0 , 1 , 3 }, // 节点2的邻居节点为0、1和3
{ 1 , 2 } // 节点3的邻居节点为1和2
};
// 深度优先搜索
void dfs ( int start , std :: vector < bool >& visited ) {
visited [ start ] = true ;
std :: cout << start << " " ;
for ( int neighbor : graph [ start ]) {
if ( ! visited [ neighbor ]) {
dfs ( neighbor , visited );
}
}
}
// 广度优先搜索
void bfs ( int start , std :: vector < bool >& visited ) {
std :: queue < int > q ;
q . push ( start );
visited [ start ] = true ;
while ( ! q . empty ()) {
int current = q . front ();
q . pop ();
std :: cout << current << " " ;
for ( int neighbor : graph [ current ]) {
if ( ! visited [ neighbor ]) {
q . push ( neighbor );
visited [ neighbor ] = true ;
}
}
}
}
int main () {
int startNode = 0 ;
std :: vector < bool > visited ( graph . size (), false );
std :: cout << "深度优先搜索结果: " ;
dfs ( startNode , visited );
std :: cout << std :: endl ;
visited . assign ( graph . size (), false );
std :: cout << "广度优先搜索结果: " ;
bfs ( startNode , visited );
std :: cout << std :: endl ;
return 0 ;
}
深度优先搜索(DFS)的优点
内存效率高:深度优先搜索(DFS)不需要额外的空间来存储节点,因此在内存使用上比广度优先搜索(BFS)更高效。 易于实现:深度优先搜索(DFS)的实现相对简单,因为它只需要递归地遍历图即可。 深度优先搜索(DFS)的缺点
可能陷入无限循环:深度优先搜索(DFS)可能会陷入无限循环,特别是在图中存在环的情况下。 可能无法找到最短路径:深度优先搜索(DFS)可能无法找到最短路径,特别 是在图中存在环的情况下。 广度优先搜索(BFS)的优点
找到最短路径:广度优先搜索(BFS)可以找到最短路径,因为它是一种按层次遍历的算法。 内存效率低:广度优先搜索(BFS)需要额外的空间来存储节点,因此在内存使用上比深度优先搜索(DFS)更差。 广度优先搜索(BFS)的缺点
可能无法找到最优解:广度优先搜索(BFS)可能无法找到最优解,特别是在图中存在环的情况下。 深度优先搜索(DFS)和广度优先搜索(BFS)都是图遍历算法,它们在不同的场景下有不同的应用。在选择使用深度优先搜索(DFS)还是广度优先搜索(BFS)时,需要根据具体情况进行选择。
动态规划 动态规划(Dynamic Programming)是一种解决复杂问题的算法思想,它通过将问题分解为子问题,并将子问题的解存储起来,以避免重复计算,从而提高算法的效率。动态规划通常用于优化问题,如最长公共子序列、最短路径等。
动态规划的基本步骤如下:
定义子问题:将原始问题分解为若干个子问题。 确定状态:确定子问题的状态,即子问题的输入和输出。 确定状态转移方程:确定子问题之间的状态转移关系。 确定初始状态:确定子问题的初始状态。 #include <iostream>
#include <vector>
int fibonacci ( int n ) {
if ( n <= 1 ) {
return n ;
}
std :: vector < int > dp ( n + 1 , 0 );
dp [ 0 ] = 0 ;
dp [ 1 ] = 1 ;
for ( int i = 2 ; i <= n ; ++ i ) {
dp [ i ] = dp [ i - 1 ] + dp [ i - 2 ];
}
return dp [ n ];
}
int main () {
int n = 10 ;
int result = fibonacci ( n );
std :: cout << "Fibonacci(" << n << ") = " << result << std :: endl ;
return 0 ;
}
动态规划的优点
高效性:动态规划可以避免重复计算,从而提高算法的效率。 可扩展性:动态规划可以方便地扩展到其他问题。 动态规划的缺点
空间复杂度高:动态规划需要存储子问题的解,因此在空间使用上可能较高。 可读性较差:动态规划的实现可能会使代码变得难以理解,特别是在状态转移方程比较复杂的情况下。 动态规划是一种强大的算法思想,适用于解决复杂问题。然而,动态规划的实现可能会导致效率较低,并且代码变得难以理解。在选择使用动态规划时,需要根据具体情况进行选择。
贪婪算法 贪婪算法(Greedy Algorithm)是一种近似解决问题的算法思想,它在每一步选择中都采取当前最优的选择,从而希望最终能够得到全局最优解。贪婪算法通常用于优化问题,如最短路径、背包问题等。
贪婪算法的基本步骤如下:
定义问题:确定要解决的问题。 确定贪心策略:确定每一步选择的贪心策略。 确定初始状态:确定子问题的初始状态。 #include <iostream>
#include <vector>
// 定义商品结构体
struct Item {
int weight ; // 商品重量
int value ; // 商品价值
};
// 贪婪算法求解背包问题
void knapsackGreedy ( std :: vector < Item >& items , int capacity ) {
int n = items . size ();
std :: vector < bool > selected ( n , false ); // 记录每个商品是否被选中
int totalWeight = 0 ; // 记录当前背包的总重量
for ( int i = 0 ; i < n ; ++ i ) {
if ( totalWeight + items [ i ]. weight <= capacity ) {
selected [ i ] = true ;
totalWeight += items [ i ]. weight ;
} else {
break ; // 背包已满,停止选择
}
}
// 输出结果
std :: cout << "Selected items: " ;
for ( int i = 0 ; i < n ; ++ i ) {
if ( selected [ i ]) {
std :: cout << "(" << items [ i ]. weight << ", " << items [ i ]. value << ") " ;
}
}
std :: cout << std :: endl ;
}
int main () {
std :: vector < Item > items = { { 10 , 60 }, { 20 , 100 }, { 30 , 120 } };
int capacity = 50 ;
knapsackGreedy ( items , capacity );
return 0 ;
}
贪婪算法的优点
高效性:贪婪算法可以在多项式时间内找到近似最优解。 贪婪算法的缺点
不保证最优解:贪婪算法可能无法找到全局最优解,只能找到近似最优解。 不适用范围广:贪婪算法通常只适用于特定类型的问题,不适用于所有问题。 贪婪算法是一种简单但高效的算法思想,适用于解决优化问题。然而,贪婪算法可能无法找到全局最优解,只能找到近似最优解。在选择使用贪婪算法时,需要根据具体情况进行选择。
排序算法 冒泡排序 冒泡排序(Bubble Sort)是一种简单的排序算法,它重复地遍历要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。
每一轮,从原乱序的数组头部开始,每两个元素比较大小并进行交换,直到这一轮当中最大或最小的元素被放置在数组的尾部,然后不断地重复这个过程,直到所有元素都排好位置。
冒泡排序(Bubble Sort)是一种简单的排序算法,它重复地遍历要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。
#include <iostream>
#include <vector>
void bubbleSort ( std :: vector < int >& arr ) {
int n = arr . size ();
for ( int i = 0 ; i < n - 1 ; ++ i ) {
for ( int j = 0 ; j < n - i - 1 ; ++ j ) {
if ( arr [ j ] > arr [ j + 1 ]) {
// 交换 arr[j] 和 arr[j + 1]
// 将比较大的元素往后移动
std :: swap ( arr [ j ], arr [ j + 1 ]);
}
}
}
}
int main () {
std :: vector < int > arr = { 64 , 34 , 25 , 12 , 22 , 11 , 90 };
bubbleSort ( arr );
std :: cout << "排序后的数组: " ;
for ( int num : arr ) {
std :: cout << num << " " ;
}
std :: cout << std :: endl ;
return 0 ;
}
冒泡排序的优点
简单易懂:冒泡排序的实现非常简单,易于理解和实现,适合初学者学习排序算法的基本概念。 稳定性:冒泡排序是一种稳定的排序算法,即相等元素的相对顺序在排序后不会改变。 冒泡排序的缺点
效率较低:冒泡排序的时间复杂度为O(n^2),其中n是要排序的元素数量。这意味着当处理大量数据时,冒泡排序的效率会非常低。 不适合大规模数据:由于其时间复杂度较高,冒泡排序不适合用于大规模数据的排序。 冒泡排序是一种简单但效率较低的排序算法,适用于小规模数据的排序或作为学习排序算法的入门示例。在实际应用中,对于大规模数据的排序,通常会使用更高效的排序算法,如快速排序、归并排序等。
插入排序 插入排序(Insertion Sort)是一种简单直观的排序算法,它的工作原理是通过从前往后构建有序序列,对于当前检查的未排序数据,在前面已排序序列中从后向前扫描,找到相应位置并插入。
#include <iostream>
#include <vector>
void insertionSort ( std :: vector < int >& arr ) {
int n = arr . size ();
for ( int i = 1 ; i < n ; ++ i ) {
int key = arr [ i ];
int j = i - 1 ;
// 将大于key的元素向后移动
while ( j >= 0 && arr [ j ] > key ) {
arr [ j + 1 ] = arr [ j ];
-- j ;
}
arr [ j + 1 ] = key ;
}
}
int main () {
std :: vector < int > arr = { 64 , 34 , 25 , 12 , 22 , 11 , 90 };
insertionSort ( arr );
std :: cout << "排序后的数组: " ;
for ( int num : arr ) {
std :: cout << num << " " ;
}
std :: cout << std :: endl ;
return 0 ;
}
前两次循环的过程图:
插入排序的优点
简单易懂:插入排序的实现非常简单,易于理解和实现,适合初学者学习排序算法的基本概念。 稳定性:插入排序是一种稳定的排序算法,即相等元素的相对顺序在排序后不会改变。 插入排序的缺点
效率较低:插入排序的时间复杂度为O(n^2),其中n是要排序的元素数量。这意味着当处理大量数据时,插入排序的效率会非常低。 不适合大规模数据:由于其时间复杂度较高,插入排序不适合用于大规模数据的排序。 插入排序是一种简单但效率较低的排序算法,适用于 小规模数据的排序 或作为学习排序算法的入门示例。在实际应用中,对于大规模数据的排序,通常会使用更高效的排序算法,如快速排序、归并排序等。
快速排序 快速排序(Quick Sort)是一种高效的排序算法,它基于分治的策略来对数组进行排序。快速排序的基本思想是选择一个基准元素,将数组分为两部分,一部分的所有元素都比基准元素小,另一部分的所有元素都比基准元素大,然后对这两部分分别进行排序。
#include <iostream>
#include <vector>
// 划分函数,选取一个基准元素,将数组分为两部分,走完之后,基准元素插入到其该在的位置,其右侧所有元素都比基准元素大,左侧所有元素都比基准元素小
int partition ( std :: vector < int >& arr , int low , int high ){
int base = arr [ high ];
int baseIndex = low ;
// 遍历数组,将所有小于基准元素的元素都移动到基准元素的左侧
for ( int i = low ; i <= high ; i ++ ){
if ( arr [ i ] < base ){
std :: swap ( arr [ i ], arr [ baseIndex ]);
baseIndex ++ ;
}
}
// 将基准元素插入到其该在的位置
std :: swap ( arr [ high ], arr [ baseIndex ]);
return baseIndex ;
}
// 递归快速排序,只要目标区域包含两个及以上的元素,就继续排序
void quickSort ( std :: vector < int >& arr , int low , int high ){
if ( low < high ){
int baseIndex = partition ( arr , low , high );
quickSort ( arr , low , baseIndex - 1 );
quickSort ( arr , baseIndex + 1 , high );
}
}
int main () {
std :: vector < int > arr = { 90 , 34 , 25 , 12 , 22 , 11 , 64 };
int n = arr . size ();
quickSort ( arr , 0 , n - 1 );
std :: cout << "排序后的数组: " ;
for ( int num : arr ) {
std :: cout << num << " " ;
}
std :: cout << std :: endl ;
return 0 ;
}
partition函数:选择一个基准元素(通常是数组的最后一个元素),将数组分为两部分,左边的元素都小于基准元素,右边的元素都大于基准元素。 quickSort函数:递归地对划分后的子数组进行排序。 main函数:在main函数中,我们创建了一个包含一些整数的向量,并调用quickSort函数对其进行排序。最后,我们输出排序后的数组。
首次调用的结果:
快速排序的优点
高效性:快速排序的平均时间复杂度为O(n log n),在大多数情况下比其他排序算法(如冒泡排序、插入排序等)更快。 原地排序:快速排序是一种原地排序算法,它不需要额外的存储空间来存储临时数据。 适应性:快速排序可以根据数据的分布情况进行自适应调整,对于已经部分有序的数据也能表现出较好的性能。 快速排序的缺点
不稳定性:快速排序是一种不稳定的排序算法,即相等元素的相对顺序在排序后可能会改变。 最坏情况性能:在最坏情况下 ,快速排序的时间复杂度为O(n^2),这种情况发生在数组已经有序或接近有序时。 递归深度:快速排序是一种递归算法,在处理大规模数据时,可能会导致栈溢出的问题。 快速排序是一种高效的排序算法,适用于大规模数据的排序。然而,在最坏情况下,快速排序的性能可能会受到影响,因此在实际应用中,通常会使用更稳定的排序算法,如归并排序。
归并排序 归并排序(Merge Sort)是一种分治算法,它将一个数组分成两个子数组,分别对这两个子数组进行排序,然后将它们合并成一个有序的数组。归并排序的基本思想是将数组分成两半,对每一半进行排序,然后将排序好的两半合并起来。
#include <iostream>
#include <vector>
// 归并函数,将两个有序的子数组合并成一个有序的数组
void merge ( std :: vector < int >& arr , int left , int mid , int right ){
int leftSize = mid - left + 1 ;
int rightSize = right - mid ;
std :: vector < int > leftArr ( leftSize );
std :: vector < int > rightArr ( rightSize );
// 将左右两个子数组分别复制到临时数组中
for ( int i = 0 ; i < leftSize ; i ++ ){
leftArr [ i ] = arr [ left + i ];
}
for ( int j = 0 ; j < rightSize ; j ++ ){
rightArr [ j ] = arr [ mid + 1 + j ];
}
// 合并两个有序的子数组
int i = 0 ;
int j = 0 ;
int k = left ;
while ( i < leftSize && j < rightSize ){
if ( leftArr [ i ] <= rightArr [ j ]){
arr [ k ] = leftArr [ i ];
i ++ ;
} else {
arr [ k ] = rightArr [ j ];
j ++ ;
}
k ++ ;
}
// 将剩余的元素复制到数组中
while ( i < leftSize ){
arr [ k ] = leftArr [ i ];
i ++ ;
k ++ ;
}
while ( j < rightSize ){
arr [ k ] = rightArr [ j ];
j ++ ;
k ++ ;
}
}
// 递归归并排序,只要目标区域包含两个及以上的元素,就继续排序
void mergeSort ( std :: vector < int >& arr , int left , int right ){
if ( left < right ){
int mid = left + ( right - left ) / 2 ;
mergeSort ( arr , left , mid );
mergeSort ( arr , mid + 1 , right );
merge ( arr , left , mid , right );
}
}
int main () {
std :: vector < int > arr = { 90 , 34 , 25 , 12 , 22 , 11 , 64 };
int n = arr . size ();
mergeSort ( arr , 0 , n - 1 );
std :: cout << "排序后的数组: " ;
for ( int num : arr ) {
std :: cout << num << " " ;
}
std :: cout << std :: endl ;
return 0 ;
}
归并排序的优点
稳定性:归并排序是一种稳定的排序算法,即相等元素的相对顺序在排序后不会改变。 高效性:归并排序的平均时间复杂度为O(n log n),在大多数情况下比其他排序算法(如冒泡排序、插入排序等)更快。 适应性:归并排序可以根据数据的分布情况进行自适应调整,对于已经部分有序的数据也能表现出较好的性能。 归并排序的缺点
空间开销:归并排序需要额外的空间来存储临时数据,这可能会导致空间开销较大。 递归深度:归并排序是一种递归算法,在处理大规模数据时,可能会导致栈溢出的问题。 归并排序是一种高效的排序算法,适用于小规模数据的排序。然而,在空间开销和递归深度方面,归并排序可能会受到限制。
选择排序 选择排序是一种简单直观的排序算法,它的工作原理是每次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置(末尾),然后再从剩余未排序元素中继续寻找,换位。以此类推,直到全部待排序的数据元素排完。
#include <iostream>
#include <vector>
void selectionSort ( std :: vector < int >& arr ) {
int n = arr . size ();
for ( int i = 0 ; i < n - 1 ; ++ i ) {
int minIndex = i ;
for ( int j = i + 1 ; j < n ; ++ j ) {
if ( arr [ j ] < arr [ minIndex ]) {
minIndex = j ;
}
}
std :: swap ( arr [ i ], arr [ minIndex ]);
}
}
int main () {
std :: vector < int > arr = { 64 , 25 , 12 , 22 , 11 , 90 };
selectionSort ( arr );
std :: cout << "排序后的数组: " ;
for ( int num : arr ) {
std :: cout << num << " " ;
}
std :: cout << std :: endl ;
return 0 ;
}
选择排序的优点
简单易懂:选择排序的实现非常简单,易于理解和实现,适合初学者学习排序算法的基本概念。 选择排序的缺点
效率较低:选择排序的时间复杂度为O(n^2),其中n是要排序的元素数量。这意味着当处理大量数据时,选择排序的效率会非常低。 选择排序是一种简单但效率较低的排序算法,适用于小规模数据的排序或作为学习排序算法的入门示例。
堆排序 堆排序是一种高效的排序算法,它基于堆数据结构来实现。堆排序的基本思想是将待排序的数组构建成一个最大堆(或最小堆),然后将堆顶元素(最大或最小)与堆的最后一个元素交换,然后将堆的大小减1,再调整堆,重复上述过程,直到堆的大小为1。
#include <iostream>
#include <vector>
// 调整堆,将以index为根节点的子树调整为最大堆
void heapify ( std :: vector < int >& arr , int n , int index ) {
int largest = index ;
int left = 2 * index + 1 ;
int right = 2 * index + 2 ;
if ( left < n && arr [ left ] > arr [ largest ]) {
largest = left ;
}
if ( right < n && arr [ right ] > arr [ largest ]) {
largest = right ;
}
if ( largest != index ) {
std :: swap ( arr [ index ], arr [ largest ]);
heapify ( arr , n , largest );
}
}
void heapSort ( std :: vector < int >& arr ) {
int n = arr . size ();
// 构建最大堆
for ( int i = n / 2 - 1 ; i >= 0 ; -- i ) {
heapify ( arr , n , i );
}
// 依次取出堆顶元素,并调整堆
for ( int i = n - 1 ; i >= 0 ; -- i ) {
std :: swap ( arr [ 0 ], arr [ i ]);
heapify ( arr , i , 0 );
}
}
int main () {
std :: vector < int > arr = { 64 , 25 , 12 , 22 , 11 , 90 };
heapSort ( arr );
std :: cout << "排序后的数组: " ;
for ( int num : arr ) {
std :: cout << num << " " ;
}
std :: cout << std :: endl ;
return 0 ;
}
堆排序的优点
高效性:堆排序的平均时间复杂度为O(n log n),在大多数情况下比其他排序算法(如冒泡排序、插入排序等)更快。 堆排序的缺点
不稳定性:堆排序是一种不稳定的排序算法,即相等元素的相对顺序在排序后可能会改变。 堆排序是一种高效的排序算法,适用于大规模数据的排序。然而,在最坏情况下,堆排序的性能可能会受到影响。
希尔排序 希尔排序是一种高效的排序算法,它基于插入排序的思想来实现。希尔排序的基本思想是将待排序的数组分成若干个子序列,对每个子序列进行插入排序,然后逐渐缩小子序列的间隔,直到间隔为1时,对整个数组进行一次插入排序。
#include <iostream>
#include <vector>
void shellSort ( std :: vector < int >& arr ) {
int n = arr . size ();
// 初始间隔为数组长度的一半
for ( int gap = n / 2 ; gap > 0 ; gap /= 2 ) {
// 对每个子序列进行插入排序
for ( int i = gap ; i < n ; ++ i ) {
int temp = arr [ i ];
int j ;
for ( j = i ; j >= gap && arr [ j - gap ] > temp ; j -= gap ) {
arr [ j ] = arr [ j - gap ];
}
arr [ j ] = temp ;
}
}
}
int main () {
std :: vector < int > arr = { 64 , 25 , 12 , 22 , 11 , 90 };
shellSort ( arr );
std :: cout << "排序后的数组: " ;
for ( int num : arr ) {
std :: cout << num << " " ;
}
std :: cout << std :: endl ;
return 0 ;
}
希尔排序的优点
效率较高:希尔排序的时间复杂度优于普通的插入排序(O(n²)),尤其是在中等规模的数据集上表现较好。其时间复杂度通常在O(n log² n)到O(n²)之间,具体取决于步长序列的选择。 原地排序:希尔排序不需要额外的存储空间,是一种原地排序算法。 简单易实现:希尔排序的实现相对简单,尤其是对于已经熟悉插入排序的开发者来说。 适用于中等规模数据:对于中等规模的数据集,希尔排序的性能通常优于冒泡排序和选择排序等简单排序算法。 希尔排序的缺点
时间复杂度不稳定:希尔排序的时间复杂度依赖于步长序列的选择,最坏情况下可能退化为O(n²),无法保证在所有情况下都表现良好。 不适合大规模数据:对于大规模数据集,希尔排序的效率不如快速排序、归并排序或堆排序等更高效的算法。 步长序列选择复杂:步长序列的选择对希尔排序的性能影响很大,但如何选择最优的步长序列仍然是一个研究课题,没有统一的标准。 适用场景:
中等规模的数据集。 对内存使用有严格限制的场景(因为它是原地排序)。 作为其他更复杂排序算法的初步优化步骤。 希尔排序是一种简单且有效的排序算法,尤其适用于中等规模的数据集。虽然它在最坏情况下的时间复杂度较高,但通过选择合适的步长序列,可以在实际应用中取得较好的性能。对于大规模数据集,更高效的排序算法(如快速排序或归并排序)通常是更好的选择。
计数排序 计数排序是一种非比较排序算法,它的基本思想是利用数组的下标来确定元素的正确位置。计数排序的步骤如下:
找出待排序数组中的最大值和最小值。 创建一个计数数组,数组的大小为最大值减去最小值加1。 遍历待排序数组,将每个元素出现的次数记录在计数数组中。 对计数数组进行累加,得到每个元素在排序后的数组中的正确位置。 遍历待排序数组,根据计数数组将元素放置到正确的位置上。 #include <iostream>
#include <vector>
void countingSort ( std :: vector < int >& arr ) {
int n = arr . size ();
if ( n <= 1 ) {
return ;
}
// 找出最大值和最小值
int maxVal = arr [ 0 ];
int minVal = arr [ 0 ];
for ( int i = 1 ; i < n ; ++ i ) {
if ( arr [ i ] > maxVal ) {
maxVal = arr [ i ];
}
if ( arr [ i ] < minVal ) {
minVal = arr [ i ];
}
}
// 创建计数数组
int range = maxVal - minVal + 1 ;
std :: vector < int > count ( range , 0 );
// 统计每个元素出现的次数
for ( int i = 0 ; i < n ; ++ i ) {
count [ arr [ i ] - minVal ] ++ ;
}
// 对计数数组进行累加,得到每个元素在排序后的数组中的正确位置
for ( int i = 1 ; i < range ; ++ i ) {
count [ i ] += count [ i - 1 ];
}
// 遍历待排序数组,将元素放置到正确的位置上
std :: vector < int > sortedArr ( n );
for ( int i = n - 1 ; i >= 0 ; -- i ) {
sortedArr [ count [ arr [ i ] - minVal ] - 1 ] = arr [ i ];
count [ arr [ i ] - minVal ] -- ;
}
// 将排序后的数组复制回原数组
for ( int i = 0 ; i < n ; ++ i ) {
arr [ i ] = sortedArr [ i ];
}
}
int main () {
std :: vector < int > arr = { 64 , 25 , 12 , 22 , 11 , 90 };
countingSort ( arr );
std :: cout << "排序后的数组: " ;
for ( int num : arr ) {
std :: cout << num << " " ;
}
std :: cout << std :: endl ;
return 0 ;
}
计数排序的优点
高效性:计数排序的时间复杂度为O(n + k),其中n是待排序数组的长度,k是待排序数组中元素的范围。当k不是很大时,计数排序的性能非常好。 稳定性:计数排序是一种稳定的排序算法,即相等元素的相对顺序在排序后不会改变。 计数排序的缺点
空间开销:计数排序需要额外的空间来存储计数数组,其空间复杂度为O(k),其中k是待排序数组中元素的范围。当k很大时,计数排序的空间开销可能会很大。 计数排序是一种简单且高效的排序算法,尤其适用于待排序数组中元素的范围较小的情况。它的时间复杂度为O(n + k),其中n是待排序数组的长度,k是待排序数组中元素的范围。当k不是很大时,计数排序的性能非常好。然而,计数排序的空间开销可能会很大,特别是当k很大时。
横向比较 下面是这八种排序算法时间复杂度和空间复杂度的横向比较:
查找算法 基本查找 基本查找(Linear Search)是一种简单的查找算法,它的基本思想是遍历数组,逐个比较数组元素与目标元素是否相等。如果找到相等的元素,则返回其索引;如果遍历完整个数组都没有找到相等的元素,则返回-1。
#include <iostream>
#include <vector>
// 基本查找函数
int linearSearch ( const std :: vector < int >& arr , int target ) {
int n = arr . size ();
for ( int i = 0 ; i < n ; ++ i ) {
if ( arr [ i ] == target ) {
return i ; // 找到目标元素,返回索引
}
}
return - 1 ; // 目标元素不存在
}
int main () {
std :: vector < int > arr = { 2 , 4 , 6 , 8 , 10 , 12 , 14 , 16 , 18 , 20 };
int target = 12 ;
int result = linearSearch ( arr , target );
if ( result != - 1 ) {
std :: cout << "目标元素 " << target << " 在数组中的索引为 " << result << std :: endl ;
} else {
std :: cout << "目标元素 " << target << " 不在数组中" << std :: endl ;
}
return 0 ;
}
基本查找的优点
简单易懂:基本查找的实现非常简单,易于理解和实现,适合初学者学习查找算法的基本概念。 基本查找的缺点
效率较低:基本查找的时间复杂度为O(n),其中n是数组的长度。这意味着当数组的长度较大时,基本查找的效率会非常低。 基本查找是一种简单的查找算法,适用于小规模数据的查找或作为学习查找算法的入门示例。在实际应用中,对于大规模数据的查找,通常会使用更高效的查找算法,如二分查找、哈希查找等。
二分查找 二分查找(Binary Search)是一种在有序数组中查找特定元素的搜索算法。它的基本思想是将数组分成两部分,然后比较目标元素与中间元素的大小,如果目标元素小于中间元素,则在左半部分继续查找,否则在右半部分继续查找。重复这个过程,直到找到目标元素或者确定目标元素不存在。
#include <iostream>
#include <vector>
// 二分查找函数
int binarySearch ( const std :: vector < int >& arr , int target ) {
int left = 0 ;
int right = arr . size () - 1 ;
while ( left <= right ) {
int mid = left + ( right - left ) / 2 ;
if ( arr [ mid ] == target ) {
return mid ; // 找到目标元素,返回索引
} else if ( arr [ mid ] < target ) {
left = mid + 1 ; // 目标元素在右半部分
} else {
right = mid - 1 ; // 目标元素在左半部分
}
}
return - 1 ; // 目标元素不存在
}
int main () {
std :: vector < int > arr = { 2 , 4 , 6 , 8 , 10 , 12 , 14 , 16 , 18 , 20 };
int target = 12 ;
int result = binarySearch ( arr , target );
if ( result != - 1 ) {
std :: cout << "目标元素 " << target << " 在数组中的索引为 " << result << std :: endl ;
} else {
std :: cout << "目标元素 " << target << " 不在数组中" << std :: endl ;
}
return 0 ;
}
binarySearch函数:实现了二分查找算法。它接受一个有序数组和一个目标元素作为参数,并返回目标元素在数组中的索引,如果目标元素不存在,则返回-1。 main函数:在main函数中,我们创建了一个有序数组,并调用binarySearch函数查找目标元素。最后,根据返回结果输出相应的信息。
二分查找的优点
高效性:二分查找的时间复杂度为O(log n),其中n是数组的长度。这使得它在处理大规模数据时非常高效。 简单易懂:二分查找的实现相对简单,易于理解和实现。 二分查找的缺点
要求有序:二分查找要求数组必须是有序的,如果数组无序,则需要先进行排序,这会增加时间复杂度。 不适合动态数据:如果数组中的元素经常发生变化,那么每次查找前都需要重新排序,这会导致效率低下。 二分查找是一种高效的查找算法,适用于有序数组。它的时间复杂度为O(log n),在处理大规模数据时非常高效。然而,它要求数组必须是有序的,并且不适合动态数据。
插值查找 插值查找(Interpolation Search)是一种在有序数组中查找特定元素的搜索算法。它的基本思想是根据目标元素与数组中元素的大小关系,通过 插值公式 来确定目标元素可能存在的位置,然后在该位置附近进行查找。
#include <iostream>
#include <vector>
// 插值查找函数
int interpolationSearch ( const std :: vector < int >& arr , int target ) {
int left = 0 ;
int right = arr . size () - 1 ;
while ( left <= right && target >= arr [ left ] && target <= arr [ right ]) {
if ( left == right ) {
if ( arr [ left ] == target ) {
return left ; // 找到目标元素,返回索引
}
return - 1 ; // 目标元素不存在
}
// 计算目标元素可能存在的位置
int pos = left + (( target - arr [ left ]) * ( right - left )) / ( arr [ right ] - arr [ left ]);
if ( arr [ pos ] == target ) {
return pos ; // 找到目标元素,返回索引
} else if ( arr [ pos ] < target ) {
left = pos + 1 ; // 目标元素在右半部分
} else {
right = pos - 1 ; // 目标元素在左半部分
}
}
return - 1 ; // 目标元素不存在
}
int main () {
std :: vector < int > arr = { 2 , 4 , 6 , 8 , 10 , 12 , 14 , 16 , 18 , 20 };
int target = 12 ;
int result = interpolationSearch ( arr , target );
if ( result != - 1 ) {
std :: cout << "目标元素 " << target << " 在数组中的索引为 " << result << std :: endl ;
} else {
std :: cout << "目标元素 " << target << " 不在数组中" << std :: endl ;
}
return 0 ;
}
插值查找的优点
高效性:插值查找的时间复杂度为O(log log n),其中n是数组的长度。这使得它在处理大规模数据时非常高效。 适用于均匀分布的数据:插值查找适用于均匀分布的数据,因为它根据目标元素与数组中元素的大小关系来确定目标元素可能存在的位置,从而提高了查找效率。 插值查找的缺点
要求有序:插值查找要求数组必须是有序的,如果数组无序,则需要先进行排序,这会增加时间复杂度。 插值查找是一种高效的查找算法,适用于有序数组。它的时间复杂度为O(log log n),在处理大规模数据时非常高效。然而,它要求数组必须是有序的,并且不适合动态数据。
斐波那契查找 斐波那契查找(Fibonacci Search)是一种在有序数组中查找特定元素的搜索算法。它的基本思想是利用斐波那契数列来确定目标元素可能存在的位置,然后在该位置附近进行查找。
#include <iostream>
#include <vector>
// 斐波那契查找函数
int fibonacciSearch ( const std :: vector < int >& arr , int target ) {
int n = arr . size ();
int fib2 = 0 ; // (Fibonacci(n)-1)
int fib1 = 1 ; // Fibonacci(n)
int fib = fib2 + fib1 ;
// 找到大于等于数组长度的最小斐波那契数
while ( fib < n ) {
fib2 = fib1 ;
fib1 = fib ;
fib = fib2 + fib1 ;
}
int offset = - 1 ;
while ( fib > 1 ) {
int i = std :: min ( offset + fib2 , n - 1 );
if ( arr [ i ] < target ) {
fib = fib1 ;
fib1 = fib2 ;
fib2 = fib - fib1 ;
offset = i ;
} else if ( arr [ i ] > target ) {
fib = fib2 ;
fib1 = fib1 - fib2 ;
fib2 = fib - fib1 ;
} else {
return i ; // 找到目标元素,返回索引
}
}
if ( fib1 && arr [ offset + 1 ] == target ) {
return offset + 1 ; // 找到目标元素,返回索引
}
return - 1 ; // 目标元素不存在
}
int main () {
std :: vector < int > arr = { 2 , 4 , 6 , 8 , 10 , 12 , 14 , 16 , 18 , 20 };
int target = 12 ;
int result = fibonacciSearch ( arr , target );
if ( result != - 1 ) {
std :: cout << "目标元素 " << target << " 在数组中的索引为 " << result << std :: endl ;
} else {
std :: cout << "目标元素 " << target << " 不在数组中" << std :: endl ;
}
return 0 ;
}
斐波那契查找的优点
高效性:斐波那契查找的时间复杂度为O(log n),其中n是数组的长度。这使得它在处理大规模数据时非常高效。 斐波那契查找的缺点
要求有序:斐波那契查找要求数组必须是有序的,如果数组无序,则需要先进行排序,这会增加时间复杂度。 斐波那契查找是一种高效的查找算法,适用于有序数组。它的时间复杂度为O(log n),在处理大规模数据时非常高效。然而,它要求数组必须是有序的,并且不适合动态数据。
分块查找 分块查找(Block Search)是一种在有序数组中查找特定元素的搜索算法。它的基本思想是将数组分成若干个块,每个块内部有序,但块之间无序。然后根据目标元素与块的边界值进行比较,确定目标元素可能存在的块,然后在该块内进行查找。
#include <iostream>
#include <vector>
// 分块查找函数
int blockSearch ( const std :: vector < int >& arr , int target ) {
int n = arr . size ();
int blockSize = std :: sqrt ( n ); // 块的大小
int numBlocks = ( n + blockSize - 1 ) / blockSize ; // 块的数量
std :: vector < int > blockMax ( numBlocks ); // 存储每个块的最大值
// 找到每个块的最大值
for ( int i = 0 ; i < numBlocks ; ++ i ) {
int blockStart = i * blockSize ;
int blockEnd = std :: min (( i + 1 ) * blockSize , n );
blockMax [ i ] = arr [ blockStart ];
for ( int j = blockStart + 1 ; j < blockEnd ; ++ j ) {
if ( arr [ j ] > blockMax [ i ]) {
blockMax [ i ] = arr [ j ];
}
}
}
// 确定目标元素可能存在的块
int blockIndex = 0 ;
while ( blockIndex < numBlocks && target > blockMax [ blockIndex ]) {
++ blockIndex ;
}
// 在目标块内进行查找
int blockStart = blockIndex * blockSize ;
int blockEnd = std :: min (( blockIndex + 1 ) * blockSize , n );
for ( int i = blockStart ; i < blockEnd ; ++ i ) {
if ( arr [ i ] == target ) {
return i ; // 找到目标元素,返回索引
}
}
return - 1 ; // 目标元素不存在
}
int main () {
std :: vector < int > arr = { 2 , 4 , 6 , 8 , 10 , 12 , 14 , 16 , 18 , 20 };
int target = 12 ;
int result = blockSearch ( arr , target );
if ( result != - 1 ) {
std :: cout << "目标元素 " << target << " 在数组中的索引为 " << result << std :: endl ;
} else {
std :: cout << "目标元素 " << target << " 不在数组中" << std :: endl ;
}
return 0 ;
}
分块查找的优点
高效性:分块查找的时间复杂度为O(sqrt(n)),其中n是数组的长度。这使得它在处理大规模数据时非常高效。 分块查找的缺点
要求有序:分块查找要求数组必须是有序的,如果数组无序,则需要先进行排序,这会增加时间复杂度。 分块查找是一种高效的查找算法,适用于有序数组。它的时间复杂度为O(sqrt(n)),在处理大规模数据时非常高效。然而,它要求数组必须是有序的,并且不适合动态数据。
哈希查找 哈希查找(Hash Search)是一种在无序数组中查找特定元素的搜索算法。它的基本思想是利用哈希函数将数组中的元素映射到一个哈希表中,然后根据目标元素的哈希值在哈希表中查找。
#include <iostream>
#include <vector>
// 哈希查找函数
int hashSearch ( const std :: vector < int >& arr , int target ) {
int n = arr . size ();
std :: vector < int > hashTable ( n , - 1 ); // 哈希表,初始化为-1
// 将数组中的元素映射到哈希表中
for ( int i = 0 ; i < n ; ++ i ) {
int hashValue = arr [ i ] % n ;
while ( hashTable [ hashValue ] != - 1 ) {
++ hashValue ;
hashValue %= n ;
}
hashTable [ hashValue ] = arr [ i ];
}
// 根据目标元素的哈希值在哈希表中查找
int hashValue = target % n ;
while ( hashTable [ hashValue ] != - 1 && hashTable [ hashValue ] != target ) {
++ hashValue ;
hashValue %= n ;
}
if ( hashTable [ hashValue ] == target ) {
return hashValue ; // 找到目标元素,返回索引
}
return - 1 ; // 目标元素不存在
}
int main () {
std :: vector < int > arr = { 2 , 4 , 6 , 8 , 10 , 12 , 14 , 16 , 18 , 20 };
int target = 12 ;
int result = hashSearch ( arr , target );
if ( result != - 1 ) {
std :: cout << "目标元素 " << target << " 在数组中的索引为 " << result << std :: endl ;
} else {
std :: cout << "目标元素 " << target << " 不在数组中" << std :: endl ;
}
return 0 ;
}
哈希查找的优点
高效性:平均时间复杂度为O(1):在理想情况下,哈希查找的时间复杂度接近常数时间,适合处理大规模数据。 快速插入和删除:哈希表不仅查找快,插入和删除操作也非常高效。 灵活性:支持多种数据类型:哈希函数可以处理不同类型的数据,如字符串、整数等。 动态扩展:哈希表可以根据需求动态调整大小,保持高效性能。 广泛应用:数据库索引:常用于数据库中的索引结构,加速数据检索。缓存系统:如Redis、Memcached等缓存系统依赖哈希表实现快速数据访问。编译器符号表:用于管理变量和函数名。 哈希查找的缺点
哈希冲突:冲突不可避免:不同键可能映射到同一位置,需通过链地址法或开放地址法解决,增加了复杂度。 性能下降:冲突过多时,查找时间可能退化为O(n)。 空间消耗:空间利用率低:为避免冲突,哈希表通常需要较大的空间,导致空间浪费。负载因子影响:负载因子过高时,冲突增加;过低时,空间浪费。 哈希函数设计复杂:设计难度:好的哈希函数需均匀分布键,减少冲突,设计较为复杂。依赖哈希函数:性能高度依赖哈希函数的质量。 不支持有序操作:无法直接排序:哈希表中的数据无序,无法直接进行范围查询或排序操作。 哈希查找在平均情况下非常高效,适合需要快速查找、插入和删除的场景。然而,哈希冲突、空间消耗和哈希函数设计的复杂性是其主要缺点。在有序操作或内存有限的情况下,可能需要考虑其他数据结构。
二叉树查找 二叉树查找(Binary Tree Search)是一种在二叉搜索树中查找特定元素的搜索算法。又指二叉搜索树(BST, Binary Search Tree)。它的核心特点是每个节点的左子树包含小于该节点的值,右子树包含大于该节点的值。
#include <iostream>
using namespace std ;
// 定义二叉树节点结构
struct TreeNode {
int val ;
TreeNode * left ;
TreeNode * right ;
TreeNode ( int x ) : val ( x ), left ( nullptr ), right ( nullptr ) {}
};
// 插入节点
TreeNode * insert ( TreeNode * root , int key ) {
if ( root == nullptr ) {
return new TreeNode ( key ); // 如果树为空,创建新节点
}
if ( key < root -> val ) {
root -> left = insert ( root -> left , key ); // 递归插入左子树
} else if ( key > root -> val ) {
root -> right = insert ( root -> right , key ); // 递归插入右子树
}
return root ;
}
// 查找节点
TreeNode * search ( TreeNode * root , int key ) {
if ( root == nullptr || root -> val == key ) {
return root ; // 找到节点或树为空
}
if ( key < root -> val ) {
return search ( root -> left , key ); // 递归查找左子树
} else {
return search ( root -> right , key ); // 递归查找右子树
}
}
// 中序遍历(用于验证树的结构)
void inorderTraversal ( TreeNode * root ) {
if ( root == nullptr ) return ;
inorderTraversal ( root -> left );
cout << root -> val << " " ;
inorderTraversal ( root -> right );
}
int main () {
TreeNode * root = nullptr ;
// 插入节点
root = insert ( root , 50 );
insert ( root , 30 );
insert ( root , 20 );
insert ( root , 40 );
insert ( root , 70 );
insert ( root , 60 );
insert ( root , 80 );
// 中序遍历输出
cout << "Inorder Traversal: " ;
inorderTraversal ( root );
cout << endl ;
// 查找节点
int key = 60 ;
TreeNode * result = search ( root , key );
if ( result != nullptr ) {
cout << "Node " << key << " found in the tree." << endl ;
} else {
cout << "Node " << key << " not found in the tree." << endl ;
}
// 查找不存在的节点
key = 90 ;
result = search ( root , key );
if ( result != nullptr ) {
cout << "Node " << key << " found in the tree." << endl ;
} else {
cout << "Node " << key << " not found in the tree." << endl ;
}
return 0 ;
}
二叉树查找的优点
查找效率较高:平均时间复杂度为O(log n):在平衡的二叉搜索树中,查找、插入和删除操作的时间复杂度为O(log n),适合中等规模的数据。 支持动态操作:插入和删除操作相对高效,适合需要频繁更新的数据集。 有序性:支持范围查询:由于二叉搜索树的中序遍历是有序的,因此可以高效地支持范围查询(如查找某个区间内的所有值)。支持排序操作:通过中序遍历可以直接得到有序数据。 结构简单:易于实现:二叉搜索树的基本操作(查找、插入、删除)实现相对简单,适合教学和基础应用。 扩展性强:可扩展为高级数据结构:二叉搜索树可以扩展为更高效的数据结构,如AVL树、红黑树、B树等,以解决平衡性问题。 缺点:
平衡性问题:最坏时间复杂度为O(n):如果树不平衡(例如退化为链表),查找、插入和删除的时间复杂度会退化为O(n)。 需要额外维护平衡:为了保持高效性,需要使用平衡二叉树(如AVL树或红黑树),增加了实现复杂度。 空间开销:每个节点需要额外存储指针:二叉树需要存储左右子节点的指针,空间开销较大,尤其是在存储大量小数据时。 不适合大规模数据:性能受限:对于大规模数据,二叉树的深度会增加,导致查找效率下降。相比之下,哈希表或B树更适合大规模数据。 动态操作可能导致性能波动:频繁插入和删除可能破坏平衡:在普通二叉搜索树中,频繁的插入和删除操作可能导致树结构失衡,影响性能。 二叉树查找在数据有序性和动态操作方面表现良好,适合中等规模且需要频繁更新和范围查询的场景。然而,其性能高度依赖于树的平衡性,普通二叉搜索树在极端情况下可能退化为链表,导致性能下降。因此,在实际应用中,通常使用平衡二叉树(如AVL树或红黑树)来保证性能稳定性。对于大规模数据或需要更高性能的场景,可能需要考虑其他数据结构(如B树或哈希表)。
本文是C++基础学习完成的进阶记录,一些高阶技法和基础补齐
前面的相关文章:
C++基础记录
C++基础记录(二)
C++基础记录(三)
【算法刷题】C++常见容器使用集合
处理器 时钟频率(Clock Speed)和内核数量(Core Count)是衡量处理器性能的两个关键指标,它们对 C++ 程序的性能影响很大,但方式各不相同。理解这两者如何协同工作,能帮助你更好地优化程序。
时钟频率对C++程序性能的影响 时钟频率通常以千兆赫兹(GHz)为单位,它 决定了处理器每个内核每秒能执行多少个操作 。一个 3.0 GHz 的处理器,意味着处理器每秒有 3.0×10 9 个时钟周期(或脉冲)。
一个时钟周期并不总是对应一条指令。现代处理器为了提高效率,通常会在一个时钟周期内执行多条指令,或者一条复杂的指令会占用多个时钟周期。
IPC (Instructions Per Cycle) 也是衡量处理器效率的关键指标。IPC 表示每个时钟周期可以执行的指令数量。一个 IPC 大于 1 的处理器比 IPC 小于 1 的处理器更高效。不同的处理器架构(如 x86, ARM)、不同的指令集和不同的程序代码,IPC 值都会有很大差异。
单线程性能: 对于单线程 的 C++ 程序,时钟频率是决定性能的最主要因素。因为程序的所有计算都集中在一个内核上,更高的时钟频率意味着每个指令的执行时间更短,程序的运行速度就越快。不适合的场景: 尽管时钟频率很重要,但它并不是万能的。如果你的程序瓶颈在于 I/O 操作(比如读写文件或网络通信),或者内存访问速度,单纯提高时钟频率的效果就不那么明显了。总结: 时钟频率直接影响 C++ 程序中串行执行部分 的性能。如果你的代码大部分是顺序执行的,没有很好地利用并行化,那么提高时钟频率会带来显著的性能提升。
内核数量对C++程序性能的影响 内核数量指的是一个处理器中独立处理单元的数量。每个内核都可以独立执行任务。
多线程性能: 内核数量主要影响多线程 C++ 程序的性能。如果你使用如 std::thread、OpenMP 或 TBB 这样的技术,将任务分解成多个可以并行执行的部分,那么更多的内核就能同时处理更多的任务,从而大幅缩短总运行时间。并行化是关键: 要利用多核的优势,你的程序必须是可并行化 的。如果你的算法本身就是串行的(比如一个简单的循环没有依赖性),那么增加再多的内核也无济于事,因为它只能在一个内核上运行。并非越多越好: 尽管多核能提升性能,但多线程编程也引入了新的挑战,比如同步(Synchronization) 、锁竞争(Lock Contention) 和数据共享 等问题。如果处理不好,这些开销反而可能导致性能下降。例如,两个线程频繁地争抢同一个锁,它们可能会大部分时间都处于等待状态,而不是真正地执行计算。总结: 内核数量决定了你的 C++ 程序能够并行处理任务的能力 。要充分利用多核优势,你需要设计并实现能有效并行化的算法。
多线程 应用程序代码总是运行在线程中。线程是一个同步执行实体,其中的语句依次执行。可将 main( )的代码视为在应用程序的主线程中执行。在这个主线程中,可以创建并行运行的线程。如果应用程序除主线程外,还包含一个或多个并行运行的线程,则被称为多线程应用程序。
线程的创建方式由操作系统决定,您可直接调用操作系统提供的 API 来创建线程。
从 C++11 起,C++规定由线程函数负责为您调用操作系统 API,这提高了多线程应用程序的可移植性。如果您编写的应用程序将在特定操作系统上运行,请了解该操作系统提供的用于编写多线程应用程序的 API。
创建线程的方式随操作系统而异,C++在头文件<thread>中提供了 std::thread,它隐藏了与平台相关的细节。如果您针对特定平台编写应用程序,最好只使用针对该操作系统的线程函数。编写 C++应用程序时,如果您希望其中的线程是可移植的,请务必了解Boost 线程库
多线程注意事项
多线程应用程序常常要求线程彼此通信,这样应用程序才能成为一个整体,而不是一系列互不关心、各自为政的线程。 另外,顺序也很重要,您不希望用户界面线程在负责整理碎片的工作线程之前结束。在有些情况下,一个线程需要等待另一个线程。例如,读取数据库的线程应等待写入数据库的线程结束。 让一个线程等待另一个线程被称为线程同步。 线程的创建 C++ 11 之后添加了新的标准线程库 std::thread, std::thread 在 <thread> 头文件中声明,因此使用 std::thread 时需要包含 在 <thread> 头文件。
#include <thread>
std :: thread thread_object ( callable , args ...);
callable:可调用对象,可以是函数指针、函数对象、Lambda 表达式等。 args…:传递给 callable 的参数列表。 使用函数指针创建线程 通过函数指针创建线程,这是最基本的方式:
实例
#include <iostream>
#include <thread>
void printMessage ( int count ) {
for ( int i = 0 ; i < count ; ++ i ) {
std :: cout << "Hello from thread (function pointer)! \n " ;
}
}
int main () {
std :: thread t1 ( printMessage , 5 ); // 创建线程,传递函数指针和参数
t1 . join (); // 等待线程完成
return 0 ;
}
输出结果:
Hello from thread (function pointer)!
Hello from thread (function pointer)!
Hello from thread (function pointer)!
Hello from thread (function pointer)!
Hello from thread (function pointer)!
使用函数对象创建线程 通过类中的 operator() 方法定义函数对象来创建线程:
#include <iostream>
#include <thread>
class PrintTask {
public:
void operator ()( int count ) const {
for ( int i = 0 ; i < count ; ++ i ) {
std :: cout << "Hello from thread (function object)! \n " ;
}
}
};
int main () {
std :: thread t2 ( PrintTask (), 5 ); // 创建线程,传递函数对象和参数
t2 . join (); // 等待线程完成
return 0 ;
}
输出结果:
Hello from thread (function object)!
Hello from thread (function object)!
Hello from thread (function object)!
Hello from thread (function object)!
Hello from thread (function object)!
使用 Lambda 表达式创建线程 Lambda 表达式可以直接内联定义线程执行的代码:
#include <iostream>
#include <thread>
int main () {
std :: thread t3 ([]( int count ) {
for ( int i = 0 ; i < count ; ++ i ) {
std :: cout << "Hello from thread (lambda)! \n " ;
}
}, 5 ); // 创建线程,传递 Lambda 表达式和参数
t3 . join (); // 等待线程完成
return 0 ;
}
线程管理 join() join() 用于等待线程完成执行。如果不调用 join() 或 detach() 而直接销毁线程对象,会导致程序崩溃。
detach() detach() 将线程与主线程分离,线程在后台独立运行,主线程不再等待它。
线程的传参 值传递 参数可以通过值传递给线程:
std :: thread t ( func , arg1 , arg2 );
引用传递 如果需要传递引用参数,需要使用 std::ref :
#include <iostream>
#include <thread>
void increment ( int & x ) {
++ x ;
}
int main () {
int num = 0 ;
std :: thread t ( increment , std :: ref ( num )); // 使用 std::ref 传递引用
t . join ();
std :: cout << "Value after increment: " << num << std :: endl ;
return 0 ;
}
综合实例,以下是一个完整的示例,展示了如何使用上述三种方式创建线程,并进行线程管理。
#include <iostream>
#include <thread>
using namespace std ;
// 一个简单的函数,作为线程的入口函数
void foo ( int Z ) {
for ( int i = 0 ; i < Z ; i ++ ) {
cout << "线程使用函数指针作为可调用参数 \n " ;
}
}
// 可调用对象的类定义
class ThreadObj {
public:
void operator ()( int x ) const {
for ( int i = 0 ; i < x ; i ++ ) {
cout << "线程使用函数对象作为可调用参数 \n " ;
}
}
};
int main () {
cout << "线程 1 、2 、3 独立运行" << endl ;
// 使用函数指针创建线程
thread th1 ( foo , 3 );
// 使用函数对象创建线程
thread th2 ( ThreadObj (), 3 );
// 使用 Lambda 表达式创建线程
thread th3 ([]( int x ) {
for ( int i = 0 ; i < x ; i ++ ) {
cout << "线程使用 lambda 表达式作为可调用参数 \n " ;
}
}, 3 );
// 等待所有线程完成
th1 . join (); // 等待线程 th1 完成
th2 . join (); // 等待线程 th2 完成
th3 . join (); // 等待线程 th3 完成
return 0 ;
}
以上代码的输出结果在不同平台或每次运行时可能不同,因为线程的执行顺序由操作系统的调度算法决定,多个线程会并发运行,输出可能交错,例如:
线程 1 、 2 、 3 独立运行
线程使用函数指针作为可调用参数
线程使用函数对象作为可调用参数
线程使用 lambda 表达式作为可调用参数
线程使用函数指针作为可调用参数
按照自己对于Java线程的理解,写出了下面这段代码,期望看到两个线程交替打印。
#include <iostream>
#include <thread>
void PrintStrings () {
for ( int i = 0 ; i < 5 ; i ++ ) {
std :: cout << "Hello, World! from thread " << std :: endl ;
}
}
int main () {
std :: thread t ( PrintStrings );
t . join ();
for ( int i = 0 ; i < 5 ; i ++ ) {
std :: cout << "Hello, World! from main()" << std :: endl ;
}
return 0 ;
}
问题 :子线程内部打印完了才往下执行main内的打印。
原因 : t.join() 的作用是阻塞(block)主线程 main(),让它停下来,等待子线程 t 执行完毕。只有当子线程 t 中的 PrintStrings() 函数完全执行完成、线程终止后,main() 函数才会继续执行 t.join() 后面的代码,也就是你看到的第二个 for 循环。
解决思路就是弄清楚线程是什么时候开始执行的。
尝试将 join() 移到最后,但是这次是main中的打印全部完成,再开启子线程的打印。
原因 :在多线程程序中,操作系统负责在不同的线程之间切换,分配 CPU 时间片。虽然理论上主线程和子线程是并行运行的,但实际的执行顺序取决于操作系统的调度器。在更改 join() 位置后的代码中,main 线程创建子线程 t 之后,它会立即执行它自己的 for 循环。而子线程 t 什么时候真正开始运行,取决于操作系统什么时候给它分配 CPU 时间。对于一个相对简单的程序,main 线程通常会因为其优先级或调度策略的缘故,在创建子线程后立即获得 CPU 时间片,并执行自己的任务。在这个极短的时间内,main 线程的 for 循环可能已经全部执行完毕,甚至在子线程有机会开始运行之前。
解决 :两个线程的循环中插入延时, std::this_thread::sleep_for() 函数会让当前线程进入休眠,并主动放弃对 CPU 的占用。当 main 线程执行到 sleep_for 时,它会暂停一段时间,给操作系统一个机会去调度其他就绪的线程(比如你的子线程)。当主线程休眠结束后,它和子线程就会进入竞争状态,从而更有可能产生交替执行的效果。
#include <iostream>
#include <thread>
using namespace std ;
void PrintStrings () {
for ( int i = 0 ; i < 5 ; i ++ ) {
cout << "Hello, World! from thread " << endl ;
// 让出CPU
this_thread :: sleep_for ( chrono :: milliseconds ( 10 ));
}
}
int main () {
thread t ( PrintStrings );
for ( int i = 0 ; i < 5 ; i ++ ) {
cout << "Hello, World! from main()" << endl ;
// 让出CPU
this_thread :: sleep_for ( chrono :: milliseconds ( 10 ));
}
t . join ();
return 0 ;
}
线程数据通信 线程可共享变量,可访问全局数据。创建线程时,可给它提供一个指向共享对象(结构或类)的指针。
线程将数据写入其他线程能够存取的内存单元,这让线程能够共享数据,从而彼此进行通信。在磁盘碎片整理工具中,工作线程知道进度,而用户界面线程需要获悉这种信息;工作线程定期地存储进度(用整数表示的百分比),而用户界面线程可使用它来显示进度。
这种情形非常简单:一个线程创建信息,另一个线程使用它。如果多个线程读写相同的内存单元,结果将如何呢?有些线程开始读取数据时,其他线程可能还未结束写入操作,这将给数据的完整性带来威胁。这就是需要同步线程的原因所在。
使用互斥量和信号量同步线程 线程是操作系统级实体,而用来同步线程的对象也是操作系统提供的。大多数操作系统都提供了信号量(semaphore)和互斥量(mutex),供您用来同步线程。 互斥量(互斥同步对象)通常用于避免多个线程同时访问同一段代码。换句话说,互斥量指定了一段代码,其他线程要执行它,必须等待当前执行它的线程结束并释放该互斥量。接下来,下一个线程获取该互斥量,完成其工作,并释放该互斥量。从 C++11 起,C++通过类 std::mutex 提供了一种互斥量实现,这个类位于头文件 <mutex> 中。
通过使用信号量,可指定多少个线程可同时执行某个代码段。只允许一个线程访问的信号量被称为二值信号量(binary semaphore)。
互斥量(Mutex) 互斥量是一种同步原语,用于防止多个线程同时访问共享资源。当一个线程需要访问共享资源时,它首先需要锁定(lock)互斥量。如果互斥量已经被其他线程锁定,那么请求锁定的线程将被阻塞,直到互斥量被解锁(unlock)。
std::mutex:用于保护共享资源,防止数据竞争。
std :: mutex mtx ;
mtx . lock (); // 锁定互斥锁
// 访问共享资源
mtx . unlock (); // 释放互斥锁
std::lock_guard 和 std::unique_lock:自动管理锁的获取和释放。
std :: lock_guard < std :: mutex > lock ( mtx ); // 自动锁定和解锁
// 访问共享资源
互斥量的使用示例:
#include <mutex>
std :: mutex mtx ; // 全局互斥量
void safeFunction () {
mtx . lock (); // 请求锁定互斥量
// 访问或修改共享资源
mtx . unlock (); // 释放互斥量
}
int main () {
std :: thread t1 ( safeFunction );
std :: thread t2 ( safeFunction );
t1 . join ();
t2 . join ();
return 0 ;
}
锁(Locks) C++提供了多种锁类型,用于简化互斥量的使用和管理。
常见的锁类型包括:
std::lock_guard:作用域锁,当构造时自动锁定互斥量,当析构时自动解锁。 std::unique_lock:与std::lock_guard类似,但提供了更多的灵活性,例如可以转移所有权和手动解锁。 锁的使用示例:
#include <mutex>
std :: mutex mtx ;
void safeFunctionWithLockGuard () {
std :: lock_guard < std :: mutex > lk ( mtx );
// 访问或修改共享资源
}
void safeFunctionWithUniqueLock () {
std :: unique_lock < std :: mutex > ul ( mtx );
// 访问或修改共享资源
// ul.unlock(); // 可选:手动解锁
// ...
}
条件变量(Condition Variable) 条件变量用于线程间的协调,允许一个或多个线程等待某个条件的发生。它通常与互斥量一起使用,以实现线程间的同步。
std::condition_variable 用于实现线程间的等待和通知机制。
std :: condition_variable cv ;
std :: mutex mtx ;
bool ready = false ;
std :: unique_lock < std :: mutex > lock ( mtx );
cv . wait ( lock , []{ return ready ; }); // 等待条件满足
// 条件满足后执行
条件变量的使用示例:
#include <mutex>
#include <condition_variable>
std :: mutex mtx ;
std :: condition_variable cv ;
bool ready = false ;
void workerThread () {
std :: unique_lock < std :: mutex > lk ( mtx );
cv . wait ( lk , []{ return ready ; }); // 等待条件
// 当条件满足时执行工作
}
void mainThread () {
{
std :: lock_guard < std :: mutex > lk ( mtx );
// 准备数据
ready = true ;
} // 离开作用域时解锁
cv . notify_one (); // 通知一个等待的线程
}
原子操作(Atomic Operations) 原子操作确保对共享数据的访问是不可分割的,即在多线程环境下,原子操作要么完全执行,要么完全不执行,不会出现中间状态。
原子操作的使用示例:
#include <atomic>
#include <thread>
std :: atomic < int > count ( 0 );
void increment () {
count . fetch_add ( 1 , std :: memory_order_relaxed );
}
int main () {
std :: thread t1 ( increment );
std :: thread t2 ( increment );
t1 . join ();
t2 . join ();
return count ; // 应返回2
}
线程局部存储(Thread Local Storage, TLS) 线程局部存储允许每个线程拥有自己的数据副本。这可以通过thread_local关键字实现,避免了对共享资源的争用。
线程局部存储的使用示例:
#include <iostream>
#include <thread>
thread_local int threadData = 0 ;
void threadFunction () {
threadData = 42 ; // 每个线程都有自己的threadData副本
std :: cout << "Thread data: " << threadData << std :: endl ;
}
int main () {
std :: thread t1 ( threadFunction );
std :: thread t2 ( threadFunction );
t1 . join ();
t2 . join ();
return 0 ;
}
死锁(Deadlock)和避免策略 死锁发生在多个线程互相等待对方释放资源,但没有一个线程能够继续执行。避免死锁的策略包括:
总是以相同的顺序请求资源。 使用超时来尝试获取资源。 使用死锁检测算法。 线程间通信方式 std::future 和 std::promise :实现线程间的值传递。
std :: promise < int > p ;
std :: future < int > f = p . get_future ();
std :: thread t ([ & p ] {
p . set_value ( 10 ); // 设置值,触发 future
});
int result = f . get (); // 获取值
消息队列(基于 std::queue 和 std::mutex)实现简单的线程间通信。
C++17 引入了并行算法库 <algorithm>,其中部分算法支持并行执行,可以利用多核 CPU 提高性能。
#include <algorithm>
#include <vector>
#include <execution>
std :: vector < int > vec = { 1 , 2 , 3 , 4 , 5 };
std :: for_each ( std :: execution :: par , vec . begin (), vec . end (), []( int & n ) {
n *= 2 ;
});
多线程技术带来的问题 要使用多线程技术,必须妥善地同步线程,否则,您将有大量的无眠之夜。多线程应用程序面临的问题很多,下面是最常见的两个。
竞争状态 :多个线程试图写入同一项数据。哪个线程获胜?该对象处于什么状态? 死锁 :两个线程彼此等待对方结束,导致它们都处于“等待”状态,而应用程序被挂起。
妥善地同步可避免竞争状态。一般而言,线程被允许写入共享对象时,您必须格外小心,确保:
每次只能有一个线程写入; 在当前执行写入的线程结束前,不允许其他线程读取该对象。 通过确保任何情况下都不会有两个线程彼此等待,可避免死锁。为此,可使用主线程同步工作线程,也可在线程之间分配任务时,确保工作负荷分配明确。可以让一个线程等待另一个线程,但绝不要同时让后者也等待前者。
要学习多线程编程,可参阅大量有关该主题的在线文档,也可亲自动手实践。一旦掌握了这个主题,就能让 C++应用程序充分利用未来将发布的多核处理器。
Pagination © 2024. All rights reserved. LICENSE | NOTICE | CHANGELOG
Powered by Hydejack v9.2.1