【算法】数组和字符串

本文记录了近期在leetcode上刷题过程,主要是数组和字符串相关的
背景
近期决定补齐一下算法方面的知识,因为是非计算机科班出身,没有系统学过 C++数据结构和算法 这门课,在算法方面的知识很薄弱,想要从应用层往下深入就很困难。
Android 应用开发做需求时完全用不到算法,性能优化时是规避JVM内存泄漏,按照Android系统的规则来处理,相当于是在别人预设好的算法环境上来适配自己的代码。
所以打算借着刷算法题,把一些算法的实现记录下来,方便以后回顾。然后对于重难点进行系统的学习。
数组和字符串常用操作
在 C++ 算法题中,字符串(std::string)和数组(通常是 std::vector 或原生数组)是最常用的数据结构之一。熟练掌握它们的常见操作和标准库函数,可以极大提高编码效率和代码可读性。
一、字符串(std::string)的常见操作和库函数
C++ 中的字符串使用 std::string 类,定义在 <string> 头文件中。
1. 构造与初始化
#include <string>
using namespace std;
string s1; // 空字符串
string s2 = "hello"; // 从C风格字符串构造
string s3(5, 'a'); // "aaaaa"
string s4(s2); // 拷贝构造
string s5(s2, 1, 3); // 从s2的第1位置开始取3个字符 -> "ell"
2. 访问元素
char c1 = s2[1]; // 'e',不检查越界
char c2 = s2.at(1); // 'e',越界会抛出异常
int len = s2.length(); // 或 s2.size(),返回字符串长度
bool isEmpty = s2.empty();// 是否为空
3. 遍历字符串
// 无下标,用于拼接比较多
for (char c : s2) {
cout << c;
}
// 或者下标遍历
for (int i = 0; i < s2.size(); ++i) {
cout << s2[i];
}
4. 修改字符串
s2.append(" world"); // s2变为"hello world"
// append可以追加字符串,不可以追加字符类型
// 追加字符可以使用push_back
s2.push_back('!'); // s2变为"hello world!"
// 也可以使用 += 追加字符或字符串
s2 += "!";
s2.insert(5, " "); // 在第5位置插入空格 -> "hello world!"
s2.insert(s2.end(), s3.begin(), s3.end()); // 在s2末尾插入s3
s2.erase(5, 1); // 从第5位置删除1个字符
s2.replace(0, 5, "hi"); // 将[0,5)替换为"hi" -> "hi world!"
// 翻转字符串的某个区间
void reverseString(string &s, int start, int end) {
while (start < end) {
swap(s[start++], s[end--]);
}
}
// 使用库函数翻转
reverse(s2.begin(), s2.begin() + 5); // 翻转字符串的前5个字符 "hello world!" -> "olleH world!"
5. 查找与替换
size_t pos = s2.find("world"); // 查找子串,返回起始索引,找不到返回 string::npos
if (pos != string::npos) {
cout << "Found at: " << pos;
}
pos = s2.rfind("o"); // 从后往前查找
s2.replace(pos, 1, "a"); // 替换找到的字符
// 判断前缀/后缀
bool starts = s2.substr(0, 2) == "he"; // 手动判断前缀
bool startsWithHe = s2.compare(0, 2, "he") == 0; // 更标准但麻烦
// C++20起有 starts_with() 和 ends_with()
C++20 新增:
s.starts_with("he")s.ends_with("ld!")
6. 截取子串
string sub = s2.substr(6, 5); // 从第6位置开始,取5个字符 -> "world"
7. 转换大小写(需手动实现或使用算法)
标准库没有直接提供,但可以:
// 转小写/大写一般要自己写循环或者使用<cctype>
for (char &c : s2) {
c = tolower(c); // 需要 #include <cctype>
}
// 使用transform
transform(s2.begin(), s2.end(), s2.begin(), ::toupper); // 转大写
8. 字符串分割 / 拼接(通常需要自己实现或使用 stringstream)
- 拼接多个字符串可以用
+或append()或+= - 分割字符串一般用
stringstream+getline(..., delim)
示例(按空格分割):
string line = "a b c";
stringstream ss(line);
string word;
while (ss >> word) {
cout << word << endl;
}
二、数组相关操作(原生数组 vs std::vector)
1. 原生数组(C-style array)
定义与初始化
int arr[5] = {1, 2, 3, 4, 5};
int arr2[] = {10, 20, 30}; // 自动推导大小
常见操作
- 访问:
arr[i] - 长度:无法直接获取,除非额外保存 size
- 遍历:for 循环
- 排序等功能需要借助
<algorithm>中的算法,传入首尾指针
翻转一个数组的某个区间:
void reverseArray(int arr[], int start, int end) {
while (start < end) {
swap(arr[start++], arr[end--]);
}
}
2. std::vector 动态数组
定义在 <vector> 头文件中。
构造与初始化
#include <vector>
using namespace std;
vector<int> v1; // 空vector
vector<int> v2(5, 10); // 5个元素,都是10
vector<int> v3 = {1, 2, 3}; // 列表初始化
vector<int> v4(v3); // 拷贝构造
vector<int> v5(v3.begin(), v3.end()); // 用迭代器范围构造
常用操作
获取信息
int size = v1.size(); // 元素个数
bool isEmpty = v1.empty(); // 是否为空
访问元素
int first = v3[0]; // 不检查边界
int second = v3.at(1); // 检查边界,越界抛异常
int last = v3.back(); // 最后一个元素
int first2 = v3.front(); // 第一个元素
修改容器
v1.push_back(100); // 尾部插入
v1.pop_back(); // 尾部删除
v1.insert(v1.begin() + 1, 99); // 在第1位置后插入99
v1.erase(v1.begin()); // 删除第一个元素
v1.clear(); // 清空所有元素
遍历
// 下标遍历
for (int i = 0; i < v1.size(); ++i) {
cout << v1[i];
}
// 迭代器遍历
for (auto it = v1.begin(); it != v1.end(); ++it) {
cout << *it;
}
// 范围for遍历(推荐)
for (int x : v1) {
cout << x;
}
排序
#include <algorithm>
sort(v1.begin(), v1.end()); // 升序排序
sort(v1.begin(), v1.end(), greater<int>()); // 降序排序
查找
auto it = find(v1.begin(), v1.end(), 3); // 返回迭代器
if (it != v1.end()) {
cout << "Found: " << *it;
} else {
cout << "Not found";
}
去重(要先排序!)
sort(v1.begin(), v1.end());
auto last = unique(v1.begin(), v1.end()); // 把重复的移到后面,返回新逻辑结尾
v1.erase(last, v1.end()); // 真正删除后面的重复元素
二维 vector
vector<vector<int>> matrix(3, vector<int>(4, 0)); // 3行4列,全0
三、常用算法库函数()
很多操作都可以用 <algorithm> 中的函数简化:
#include <algorithm>
常用函数:
| 功能 | 函数 | 示例 |
|---|---|---|
| 排序 | sort(begin, end) | sort(v.begin(), v.end()); |
| 逆序 | reverse(begin, end) | reverse(v.begin(), v.end()); |
| 查找 | find(begin, end, val) | auto it = find(v.begin(), v.end(), 10); |
| 二分查找(必须有序) | binary_search(begin, end, val) | bool found = binary_search(v.begin(), v.end(), 10); |
| 二分查找边界 | lower_bound, upper_bound | 用于查找第一个“不小于”或“大于”的位置 |
| 最大值/最小值 | max(a, b), min(a, b),或 max_element, min_element | auto maxIt = max_element(v.begin(), v.end()); |
| 交换 | swap(a, b) | swap(v[i], v[j]); |
| 填充 | fill(begin, end, value) | fill(v.begin(), v.end(), 0); |
| 拷贝 | copy(src_begin, src_end, dest_begin) | copy(src.begin(), src.end(), dest.begin()); |
| 转换 | transform | 可对每个元素做操作 |
| 填充指定次数 | fill_n(dest_begin, count, value) |
四、总结:字符串 & 数组常用操作速查
| 数据结构 | 常用操作 | 相关头文件 |
|---|---|---|
| string | 拼接(+)、查找(find)、截取(substr)、插入/删除、遍历、长度(.size()) | <string> |
| vector | push_back/pop_back、insert/erase、sort/find、遍历、大小/容量 | <vector>, <algorithm> |
| 原生数组 | 下标访问、配合算法库函数使用 | <algorithm>, <cstring>(C风格字符串) |
| 通用算法 | sort, find, reverse, min/max, transform 等 | <algorithm> |
推荐最佳实践:
- 优先使用
std::vector而非原生数组,更安全、功能更强大。 - 熟悉
<algorithm>中的常用函数,比如 sort、find、reverse,能极大提升效率。 - 字符串操作推荐用 std::string 的成员函数,比如 find、substr、append 等。
- 注意边界条件,尤其在查找、删除、访问元素时。
最长连续递增序列
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:
输入:nums = [1,3,5,4,7]
输出:3
解释:最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为 5 和 7 在原数组里被 4 隔开。
示例 2:
输入:nums = [2,2,2,2,2]
输出:1
解释:最长连续递增序列是 [2], 长度为1。
提示:
1 <= nums.length <= 104
-109 <= nums[i] <= 109
思路1 不断记录更新
作为模拟题,翻译出:
- 维护一个变量
max_len记录当前最长连续递增子序列的长度。 - 遍历数组
nums,如果当前元素小于下一个元素,则max_len加一。 - 遇到减小的时候,就重置临时变量,待下一次连续递增子序列开始。
class Solution {
public:
int findLengthOfLCIS(vector<int>& nums) {
int n = nums.size();
if (n < 1)
return n;
int lenth = 1;
int maxLenth = 1;
for (int i = 0; i < n - 1; i++) {
if (nums[i + 1] > nums[i]) {
lenth++;
maxLenth = max(lenth, maxLenth);
} else {
lenth = 1;
}
}
return maxLenth;
}
};
最长连续序列
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
示例 2:
输入:nums = [0,3,7,2,5,8,4,6,0,1]
输出:9
示例 3:
输入:nums = [1,0,1,2]
输出:3
提示:
0 <= nums.length <= 105
-109 <= nums[i] <= 109
思路1 hashset查找
写法思路上和上一题一样,就是对照遍历的对象成了hashset。
- 先将所有元素加入到一个 hashset 中。
- 遍历数组中的每个元素,如果hashset中没有比当前元素数值小1的元素,说明当前元素是递增数列的开头节点,往后每次查加1的数值,直到加1寻找失败,断开区间,更新最大长度。
- 如果断开后找到的元素非头节点,重置长度为1
class Solution {
public:
int longestConsecutive(vector<int>& nums) {
int n = nums.size();
if (n < 1) {
return n;
}
unordered_set<int> tempSet;
for (int val : nums) {
tempSet.insert(val);
}
int lenth = 1;
int maxLenth = 1;
for (const int& num : tempSet) {
// 当前元素是前驱元素
if (!tempSet.count(num - 1)) {
int curretnNum = num;
while (tempSet.count(curretnNum + 1)) {
lenth++;
curretnNum += 1;
maxLenth = max(maxLenth, lenth);
}
}
// 非前驱元素了,重置lenth
lenth = 1;
}
return maxLenth;
}
};
思路2 排序后遍历
先排序原数组,再从头遍历,记录当前连续递增序列的长度,遇到断开了,就更新最大长度。
class Solution {
public:
int longestConsecutive(vector<int>& nums) {
// 处理边界情况:数组为空或只有一个元素
int max = 0, length = 0;
if (nums.size() <= 1) {
return nums.size() ? 1 : 0; // 空数组返回0,单元素返回1
}
// 先对数组进行排序,将可能连续的数字放在一起
std::sort(nums.begin(), nums.end());
// 遍历排序后的数组,寻找连续序列
for (int i = 0; i < nums.size() - 1; i++) {
// 如果相邻元素差值为1,说明是连续序列
if (nums[i + 1] - nums[i] == 1) {
length++; // 当前连续序列长度加1
}
// 如果相邻元素相等,跳过重复元素,继续检查下一个
if (nums[i + 1] == nums[i]) {
continue;
}
// 如果相邻元素差值不为1,说明连续序列中断
if (nums[i + 1] - nums[i] != 1) {
// 更新最大长度(length是间隔数,序列长度需要+1)
if (length + 1 > max) {
max = length + 1;
}
length = 0; // 重置当前序列长度
}
}
// 检查最后一个连续序列(循环结束时可能还有未统计的序列)
if (length + 1 > max) {
max = length + 1;
}
// 返回最大长度,如果max为0说明没有连续序列,返回1(至少有一个元素)
return max ? max : 1;
}
};
有趣的注入现象
这个 atexit 函数覆盖了力扣系统写入的运行时间文件:
- 力扣先执行:写入真实运行时间 → display_runtime.txt
- 程序退出时你的代码执行:写入 “0” → display_runtime.txt(覆盖之前的内容)
int init = atexit([]()
{
//力扣是从main开始进行计算的,这里先调用过ofstream让他初始化好,后面就不需要初始化了,结果会更快
ofstream("display_runtime.txt") << "0";
});
合并两个有序数组
给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n,分别表示 nums1 和 nums2 中的元素数目。
请你 合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。
注意:最终,合并后数组不应由函数返回,而是存储在数组 nums1
中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m
个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
示例 1:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
解释:需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ,其中斜体加粗标注的为 nums1 中的元素。
示例 2:
输入:nums1 = [1], m = 1, nums2 = [], n = 0
输出:[1]
解释:需要合并 [1] 和 [] 。
合并结果是 [1] 。
示例 3:
输入:nums1 = [0], m = 0, nums2 = [1], n = 1
输出:[1]
解释:需要合并的数组是 [] 和 [1] 。
合并结果是 [1] 。
注意,因为 m = 0 ,所以 nums1 中没有元素。nums1 中仅存的 0
仅仅是为了确保合并结果可以顺利存放到 nums1 中。
提示:
nums1.length == m + n
nums2.length == n
0 <= m, n <= 200
1 <= m + n <= 200
-109 <= nums1[i], nums2[j] <= 109
进阶:你可以设计实现一个时间复杂度为 O(m + n) 的算法解决此问题吗?
思路1 模拟题 从后往前遍历比较
从后往前只遍历一次,将两个数组的有效位一起拿来比较,如果一个数组的有效位使用完了,就设置为负的最小值来比较:
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int idxm = m - 1;
int idxn = n - 1;
for (int i = m + n - 1; i >= 0; i--) {
int currentm = idxm >= 0 ? nums1[idxm] : -INT_MAX;
int currentn = idxn >= 0 ? nums2[idxn] : -INT_MAX;
currentm > currentn ? idxm-- : idxn--;
nums1[i] = max(currentm, currentn);
}
}
};
思路2 优化思路1中的极值写法
使用 -INT_MAX 来作为比较值不太优雅,优化判断条。
可以填充为nums1有效位的情况是, (nums1中元素没有走完) && (nums2中元素比nums1小 || nums2已经走完了)
剩下的情况就填充nums2的有效位。
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int idxm = m - 1;
int idxn = n - 1;
for (int i = m + n - 1; i >= 0; i--) {
if (idxm >= 0 && (idxn < 0 || nums1[idxm] > nums2[idxn])) {
nums1[i] = nums1[idxm--];
} else {
nums1[i] = nums2[idxn--];
}
}
}
};
思路3 从后往前填充 判断条件不同
因为nums1空间足够,可以直接两个数组一起对比遍历,从后往前遍历,每次取两个数组中较大的一个,放到nums1的最后面。
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int i = m - 1, j = n - 1, k = m + n - 1;
while (i >= 0 && j >= 0) {
if (nums1[i] > nums2[j]) {
nums1[k--] = nums1[i--];
} else {
nums1[k--] = nums2[j--];
}
}
// 如果nums2还有剩余元素
while (j >= 0) {
nums1[k--] = nums2[j--];
}
}
};
如果第一个数组有效位比第二个数组多,那么第一个循环走完,整个nums1其实已经是自动排完序的了;
如果第二个数组元素比第一个数组有效位多,那么第一个循环走完,第二个数组还有剩余的元素,而且这些剩余元素都是最小的,第二遍循环将这些元素直接放到nums1的前面即可。
思路4 使用sort库函数
将第二个数组添加到第一个数组尾部,直接调用sort方法。
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
for (int i = 0; i != n; ++i) {
nums1[m + i] = nums2[i];
}
sort(nums1.begin(), nums1.end());
}
};
移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。
假设 nums 中不等于 val 的元素数量为 k,要通过此题,您需要执行以下操作:
更改 nums 数组,使 nums 的前 k 个元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。
返回 k。
用户评测:
评测机将使用以下代码测试您的解决方案:
int[] nums = [...]; // 输入数组
int val = ...; // 要移除的值
int[] expectedNums = [...]; // 长度正确的预期答案。
// 它以不等于 val 的值排序。
int k = removeElement(nums, val); // 调用你的实现
assert k == expectedNums.length;
sort(nums, 0, k); // 排序 nums 的前 k 个元素
for (int i = 0; i < actualLength; i++) {
assert nums[i] == expectedNums[i];
}
如果所有的断言都通过,你的解决方案将会 通过。
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2,_,_]
解释:你的函数函数应该返回 k = 2, 并且 nums 中的前两个元素均为 2。
你在返回的 k 个元素之外留下了什么并不重要(因此它们并不计入评测)。
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3,_,_,_]
解释:你的函数应该返回 k = 5,并且 nums 中的前五个元素为 0,0,1,3,4。
注意这五个元素可以任意顺序返回。
你在返回的 k 个元素之外留下了什么并不重要(因此它们并不计入评测)。
提示:
0 <= nums.length <= 100
0 <= nums[i] <= 50
0 <= val <= 100
思路1 双指针
快慢指针,题目要求原地移除所有等于val的元素。快指针往前遍历,慢指针代表留存元素的位置。快指针的值不等于要移除元素时,说明这个值需要留存,将快指针的值复制到慢指针指向的位置,快慢指针同时往前;当快指针指向了要移除的元素时,此时慢指针一定也指向了要移除的元素,慢指针不动,此位置要接受下一个留存的值,只移动快指针。
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int n = nums.size();
int left = 0;
for (int right = 0; right < n; right++) {
if (nums[right] != val) {
nums[left] = nums[right];
left++;
}
}
return left;
}
};
删除有序数组中的重复项
给你一个 非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题解可以被通过:
更改数组 nums ,使 nums 的前 k 个元素包含唯一元素,并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
返回 k 。
判题标准:
系统会用下面的代码来测试你的题解:
int[] nums = [...]; // 输入数组
int[] expectedNums = [...]; // 长度正确的期望答案
int k = removeDuplicates(nums); // 调用
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums[i] == expectedNums[i];
}
如果所有断言都通过,那么您的题解将被 通过。
示例 1:
输入:nums = [1,1,2]
输出:2, nums = [1,2,_]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
提示:
1 <= nums.length <= 3 * 104
-104 <= nums[i] <= 104
nums 已按 非严格递增 排列
思路1 双指针
和上一题类似,快慢指针,快指针遍历数组,慢指针代表不重复元素的位置。快指针遍历到的元素如果和慢指针指向的元素不同,说明这个元素是不重复的,将快指针指向的元素复制到慢指针指向的位置,快慢指针同时往前;如果快指针指向的元素和慢指针指向的元素相同,说明这个元素是重复的,只移动快指针。慢指针停留在此处等待写入新的不重复元素。
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
int n = nums.size();
int left = 0;
for (int right = 0; right < n; right++) {
if (nums[right] != nums[left]) {
left++;
nums[left] = nums[right];
}
}
// left 是下标,加1为长度
return left + 1;
}
};
删除有序数组中的重复项 II
给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使得出现次数超过两次的元素只出现两次 ,返回删除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参做任何拷贝
int len = removeDuplicates(nums);
// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
print(nums[i]);
}
示例 1:
输入:nums = [1,1,1,2,2,3]
输出:5, nums = [1,1,2,2,3]
解释:函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3。 不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,1,2,3,3]
输出:7, nums = [0,0,1,1,2,3,3]
解释:函数应返回新长度 length = 7, 并且原数组的前七个元素被修改为 0, 0, 1, 1, 2, 3, 3。不需要考虑数组中超出新长度后面的元素。
提示:
1 <= nums.length <= 3 * 104
-104 <= nums[i] <= 104
nums 已按升序排列
思路1 双指针
处理后的数组最短长度一定比2大,因为每个元素最多出现两次。所以短数组特殊处理,快慢指针起点直接从下标2开始。较上一题基础题,唯一的不同就是处理好留存元素和位置的判断条件。
这里因为是有序数组,所以从慢指针的前两个元素进行判断,表示当前元素是否和前两个元素重复。如果重复,说明当前元素需要被删除,只移动快指针;如果不重复,说明当前元素需要被保留,将快指针指向的元素复制到慢指针指向的位置,快慢指针同时往前。
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
int n = nums.size();
if (n <= 2) {
return n;
}
int slow = 2, fast = 2;
while (fast < n) {
if (nums[slow - 2] != nums[fast]) {
nums[slow] = nums[fast];
++slow;
}
++fast;
}
return slow;
}
};
多数元素
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:nums = [3,2,3]
输出:3
示例 2:
输入:nums = [2,2,1,1,1,2,2]
输出:2
提示:
n == nums.length
1 <= n <= 5 * 104
-109 <= nums[i] <= 109
思路1 哈希表
用哈希表记录每个元素出现的次数,遍历哈希表,找到出现次数大于n/2的元素。
class Solution {
public:
int majorityElement(vector<int>& nums) {
int n = nums.size();
unordered_map<int, int> map;
for (int i = 0; i < n; i++) {
map[nums[i]]++;
}
for (auto it = map.begin(); it != map.end(); it++) {
if (it->second > n / 2) {
return it->first;
}
}
return -1;
}
};
找到出现次数最多的元素
如果不一定有出现次数大于 n/2 的元素,而是需要是找出现次数最多的元素 。相较于思路1,只需要遍历哈希表时,不断交换最大值,找到出现次数最多的元素即可。
class Solution {
public:
int majorityElement(vector<int>& nums) {
int n = nums.size();
unordered_map<int, int> map;
for (int i = 0; i < n; i++) {
map[nums[i]]++;
}
int max = 0;
int maxItem = nums[0];
for (auto it = map.cbegin(); it != map.cend(); it++) {
if (it->second > max) {
maxItem = it->first;
max = it->second;
}
}
return maxItem;
}
};
排序后直接取中点的元素
如果将数组 nums 中的所有元素按照单调递增或单调递减的顺序排序,那么下标为 n/2 的元素(下标从 0 开始)一定是众数。
class Solution {
public:
int majorityElement(vector<int>& nums) {
int n = nums.size();
sort(nums.begin(), nums.end());
return nums[n/2];
}
};
轮转数组
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入:nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
提示:
1 <= nums.length <= 105
-231 <= nums[i] <= 231 - 1
0 <= k <= 105
思路1 使用额外的数组直接承接
因为k有可能是大于n的,即有可能轮换一整轮还要多。所以原数组中,每个的元素位置为 k + i % n 取余。
class Solution {
public:
void rotate(vector<int>& nums, int k) {
int n = nums.size();
vector<int> temp(n);
for (int i = 0; i < n; i++) {
temp[(k + i) % n] = nums[i];
}
nums = temp;
}
};
思路2 上一个方案的变体
直接拼接nums两遍,找到轮转后的起始位置,从这里取值,取n次填到原数组中去。
class Solution {
public:
void rotate(vector<int>& nums, int k) {
int n = nums.size(); // 获取数组的长度
// 创建一个临时数组 temp,并将原数组 nums 的内容拷贝进去
vector<int> temp = nums;
// 关键步骤:将原数组 nums 再次拼接到 temp 后面
// 这样就可以通过选取合适的起始位置,来得到旋转后的数组
temp.insert(temp.end(), nums.begin(), nums.end());
// 计算旋转的起始位置:
// 我们想把原数组向右旋转 k 个位置。
// 为了便于计算,我们令 start = n - k % n
// 注意:k 可能大于 n,所以要取模:k % n
int start = n - k % n;
// 这 n 个连续元素,就是原数组旋转 k 次后的正确顺序
for (int i = 0; i < n; i++) {
nums[i] = temp[start + i];
}
}
};
思路3 三次反转
流程如下表:
| 操作 | 结果 |
|---|---|
| 原始数组 | 1 2 3 4 5 6 7 |
| 翻转所有元素 | 7 6 5 4 3 2 1 |
翻转 [0,kmodn−1] 区间的元素 | 5 6 7 4 3 2 1 |
翻转 [kmodn,n−1] 区间的元素 | 5 6 7 1 2 3 4 |
class Solution {
public:
void reverse(vector<int>& nums, int left, int right) {
while (left < right) {
swap(nums[left], nums[right]);
left++;
right--;
}
}
void rotate(vector<int>& nums, int k) {
int n = nums.size();
k %= n;
reverse(nums.begin(), nums.end());
reverse(nums.begin(), nums.begin() + k);
reverse(nums.begin() + k, nums.end());
}
};
字符串轮转
要求同上,将数组改为字符串:
class Solution {
public:
void rotate(string& str, int k) {
int n = str.size();
string temp = str + str;
int start = n - k % n;
str = temp.substr(start, n);
}
};
字符串的方法比数组简单,直接使用加号拼接,使用 substr 来取范围。
买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 105
0 <= prices[i] <= 104
思路1 一次遍历
从左往右,碰到最小的就更新 min 值,代表买入时机。碰到差值最大的就更新 maxProfit 值,代表所能赚取的最大利润。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int min = 10000;
int maxProfit = 0;
int n = prices.size();
for (int i = 0; i < n; i++) {
if (prices[i] < min) {
min = prices[i];
} else if (prices[i] - min > maxProfit) {
maxProfit = prices[i] - min;
}
}
return maxProfit;
}
};
买卖股票的最佳时机 II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。然而,你可以在 同一天 多次买卖该股票,但要确保你持有的股票不超过一股。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3。
最大总利润为 4 + 3 = 7 。
示例 2:
输入:prices = [1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4。
最大总利润为 4 。
示例 3:
输入:prices = [7,6,4,3,1]
输出:0
解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0。
提示:
1 <= prices.length <= 3 * 104
0 <= prices[i] <= 104
思路1 一次遍历
从左往右,碰到比前一天价格高的,就计算利润并加入到总利润中。即拥有所有收益,避开所有亏损, 这个计算方式和最优的买入卖出操作效果等价 。
class Solution {
public:
int maxProfit(vector<int>& prices) {
int maxProfit = 0;
int n = prices.size();
for (int i = 1; i < n; i++) {
if (prices[i] > prices[i - 1]) {
maxProfit += prices[i] - prices[i - 1];
}
}
return maxProfit;
}
};
跳跃游戏
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
提示:
1 <= nums.length <= 104
0 <= nums[i] <= 105
思路1 贪心
根据题目的描述,只要存在一个位置 x,它本身可以到达,并且它跳跃的最大长度为 x+nums[x],这个值大于等于 y,即 x+nums[x]≥y,那么位置 y 也可以到达。
满足可达的条件之后,不断更新 x+nums[x] 这个最远可达的位置,最终这个值越过或者可以到达最后一个下标即为成功,否则失败。
class Solution {
public:
bool canJump(vector<int>& nums) {
int n = nums.size();
int rightmost = 0;
for (int i = 0; i < n; ++i) {
// 判断当前位置 i 是否可达
if (i <= rightmost) {
// 更新最远可达位置
rightmost = max(rightmost, i + nums[i]);
// 如果最远可达位置大于等于最后一个下标,返回 true
if (rightmost >= n - 1) {
return true;
}
}
}
// 如果遍历完成,最远可达位置还不到最后一个下标,返回 false
return false;
}
};
跳跃游戏 II
给定一个长度为 n 的 0 索引整数数组 nums。初始位置在下标 0。
每个元素 nums[i] 表示从索引 i 向后跳转的最大长度。换句话说,如果你在索引 i 处,你可以跳转到任意 (i + j) 处:
0 <= j <= nums[i] 且 i + j < n
返回到达 n - 1 的最小跳跃次数。测试用例保证可以到达 n - 1。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
提示:
1 <= nums.length <= 104
0 <= nums[i] <= 1000
题目保证可以到达 n - 1
思路1 贪心 正向查找
每次到达某个位置时,计算可达位置之后可以跳跃的最远距离,记录下这个最远距离,当到达这个最远距离时,跳跃次数加一。 不管内部选取哪一个点作为下一个起跳点,经过这个最远边界时,一定只需要增加跳跃一次 。
在遍历数组时,我们不访问最后一个元素,这是因为在访问最后一个元素之前,我们的边界一定大于等于最后一个位置,否则就无法跳到最后一个位置了。如果访问最后一个元素,在边界正好为最后一个位置的情况下,我们会增加一次「不必要的跳跃次数」,因此我们不必访问最后一个元素。
class Solution {
public:
int jump(vector<int>& nums) {
int maxPos = 0, n = nums.size(), end = 0, step = 0;
for (int i = 0; i < n - 1; i++) {
if (i <= maxPos) {
maxPos = max(maxPos, i + nums[i]);
if (end == i) {
end = maxPos;
step++;
}
}
}
return step;
}
};
H指数
给你一个整数数组 citations ,其中 citations[i] 表示研究者的第 i 篇论文被引用的次数。计算并返回该研究者的 h 指数。
根据维基百科上 h 指数的定义:h 代表“高引用次数” ,一名科研人员的 h 指数 是指他(她)至少发表了 h 篇论文,并且 至少 有 h 篇论文被引用次数大于等于 h 。如果 h 有多种可能的值,h 指数 是其中最大的那个。
示例 1:
输入:citations = [3,0,6,1,5]
输出:3
解释:给定数组表示研究者总共有 5 篇论文,每篇论文相应的被引用了 3, 0, 6, 1, 5 次。
由于研究者有 3 篇论文每篇 至少 被引用了 3 次,其余两篇论文每篇被引用 不多于 3 次,所以她的 h 指数是 3。
示例 2:
输入:citations = [1,3,1]
输出:1
提示:
n == citations.length
1 <= n <= 5000
0 <= citations[i] <= 1000
思路1 两遍遍历
按照题目描述的计算规则写逻辑即可,O(n^2) 的时间复杂度。
class Solution {
public:
int hIndex(vector<int>& citations) {
int n = citations.size(), hIndex = 0;
for (int i = 0; i < n; i++) {
int count = 0;
for (int j = 0; j < n; j++) {
if (citations[i] <= citations[j] && citations[i] > count) {
count++;
}
}
hIndex = max(hIndex, count);
}
return hIndex;
}
};
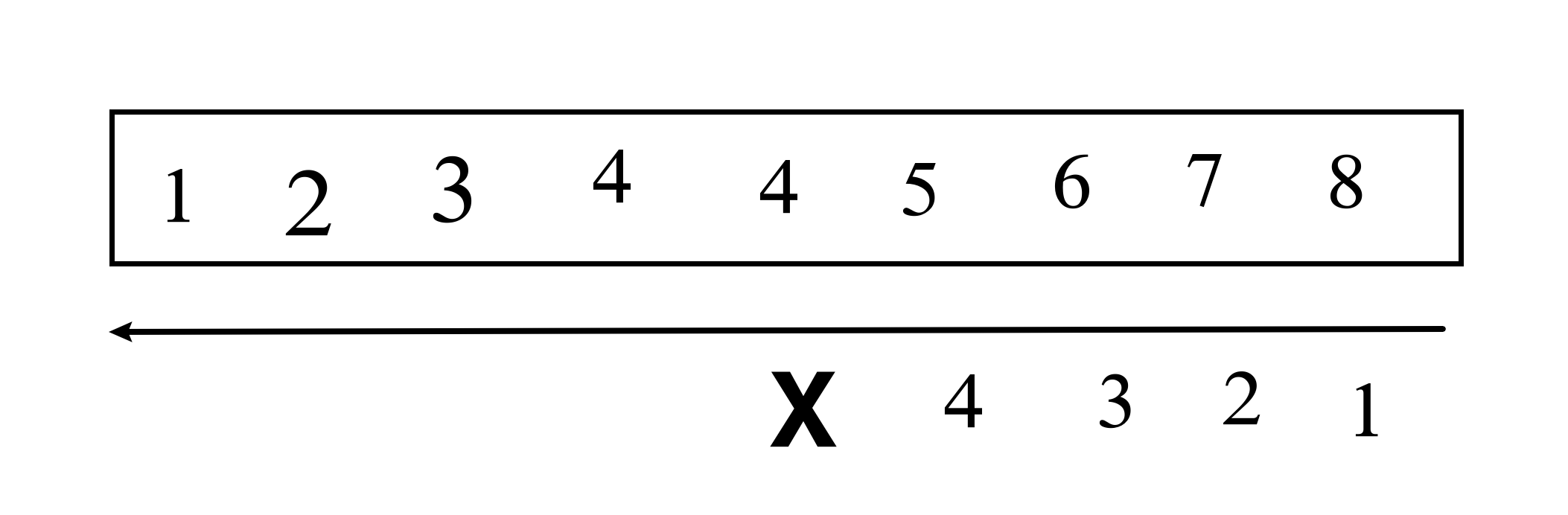
排序后逆序遍历
根据 H 指数的定义,如果当前 H 指数为 h 并且在遍历过程中找到当前值 citations[i]>h,则说明我们找到了一篇被引用了至少 h+1 次的论文,所以将现有的 h 值加 1。继续遍历直到 h 无法继续增大。最后返回 h 作为最终答案。
class Solution {
public:
int hIndex(vector<int>& citations) {
int hIndex = 0, i = citations.size() - 1;
sort(citations.begin(), citations.end());
while (i >= 0 && citations[i] > hIndex) {
hIndex++;
i--;
}
return hIndex;
}
};
O(1) 时间插入、删除和获取随机元素
实现RandomizedSet 类:
RandomizedSet() 初始化 RandomizedSet 对象
bool insert(int val) 当元素 val 不存在时,向集合中插入该项,并返回 true ;否则,返回 false 。
bool remove(int val) 当元素 val 存在时,从集合中移除该项,并返回 true ;否则,返回 false 。
int getRandom() 随机返回现有集合中的一项(测试用例保证调用此方法时集合中至少存在一个元素)。每个元素应该有 相同的概率 被返回。
你必须实现类的所有函数,并满足每个函数的 平均 时间复杂度为 O(1) 。
示例:
输入
["RandomizedSet", "insert", "remove", "insert", "getRandom", "remove", "insert", "getRandom"]
[[], [1], [2], [2], [], [1], [2], []]
输出
[null, true, false, true, 2, true, false, 2]
解释
RandomizedSet randomizedSet = new RandomizedSet();
randomizedSet.insert(1); // 向集合中插入 1 。返回 true 表示 1 被成功地插入。
randomizedSet.remove(2); // 返回 false ,表示集合中不存在 2 。
randomizedSet.insert(2); // 向集合中插入 2 。返回 true 。集合现在包含 [1,2] 。
randomizedSet.getRandom(); // getRandom 应随机返回 1 或 2 。
randomizedSet.remove(1); // 从集合中移除 1 ,返回 true 。集合现在包含 [2] 。
randomizedSet.insert(2); // 2 已在集合中,所以返回 false 。
randomizedSet.getRandom(); // 由于 2 是集合中唯一的数字,getRandom 总是返回 2 。
提示:
-231 <= val <= 231 - 1
最多调用 insert、remove 和 getRandom 函数 2 * 105 次
在调用 getRandom 方法时,数据结构中 至少存在一个 元素。
思路1 哈希表 + 数组
要求实现 O(1) 时间的插入、删除和获取随机元素操作。已知哈希表的搜索元素复杂度是 O(1) ,即插入删除很快,但是无下标,无法完成随机获取元素。而动态数组可以根据下标随机获取元素,但是插入和删除,搜索元素的复杂度是O(n),可以将二者结合起来,数组用来实际的存储元素,哈希表来记录下标和元素值。
class RandomizedSet {
public:
RandomizedSet() {
srand((unsigned)time(NULL));
}
bool insert(int val) {
if (indices.count(val)) {
return false;
}
int index = nums.size();
nums.emplace_back(val);
indices[val] = index;
return true;
}
bool remove(int val) {
if (!indices.count(val)) {
return false;
}
int index = indices[val];
int last = nums.back();
nums[index] = last;
indices[last] = index;
nums.pop_back();
indices.erase(val);
return true;
}
int getRandom() {
// 测试用例保证调用此方法时集合中至少存在一个元素
int randomIndex = rand()%nums.size();
return nums[randomIndex];
}
private:
vector<int> nums;
unordered_map<int, int> indices;
};
srand((unsigned)time(NULL)); 根据程序运行时间,生成随机数种子。rand() 函数根据这个种子生成随机数。如果不设置种子,rand() 函数会根据一个默认的种子生成随机数,这会导致每次运行程序时生成的随机数序列相同。
- 插入操作时,首先判断 val 是否在哈希表中,如果已经存在则返回 false,如果不存在则插入 val,操作如下:
- 如果 val 不在哈希表中,将 val 插入变长数组的末尾;
- 在添加 val 之前的变长数组长度为 val 所在下标 index,将 val 和下标 index 存入哈希表;
- 返回 true。
- 删除操作时,首先判断 val 是否在哈希表中,如果不存在则返回 false,如果存在则删除 val,操作如下:
- 从哈希表中获得 val 的下标 index;
- 将变长数组的最后一个元素 last 移动到下标 index 处,在哈希表中将 last 的下标更新为 index;
- 在变长数组中删除最后一个元素,在哈希表中删除 val;
- 返回 true。
删除操作的重点在于将变长数组的最后一个元素移动到待删除元素的下标处,然后删除变长数组的最后一个元素。该操作的时间复杂度是 O(1),且可以保证在删除操作之后变长数组中的所有元素的下标都连续,方便插入操作和获取随机元素操作。
- 获取随机元素操作时,由于变长数组中的所有元素的下标都连续,因此随机选取一个下标,返回变长数组中该下标处的元素。
除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法,且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:
输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]
提示:
2 <= nums.length <= 105
-30 <= nums[i] <= 30
输入 保证 数组 answer[i] 在 32 位 整数范围内
进阶:你可以在 O(1) 的额外空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组 不被视为 额外空间。)
思路1 左右乘积列表
我们不必将所有数字的乘积除以给定索引处的数字得到相应的答案,而是利用索引左侧所有数字的乘积和右侧所有数字的乘积(即前缀与后缀)相乘得到答案。
对于给定索引 i,我们将使用它左边所有数字的乘积乘以右边所有数字的乘积。下面让我们更加具体的描述这个算法。
算法步骤:
初始化两个空数组 L 和 R。对于给定索引 i,L[i] 代表的是 i 左侧所有数字的乘积,R[i] 代表的是 i 右侧所有数字的乘积。 我们需要用两个循环来填充 L 和 R 数组的值。
- 对于数组 L,
L[0]应该是 1,因为第一个元素的左边没有元素。对于其他元素:L[i] = L[i-1] * nums[i-1]。 - 同理,对于数组 R,
R[length-1]应为 1。length 指的是输入数组的大小。其他元素:R[i] = R[i+1] * nums[i+1]。
当 R 和 L 数组填充完成,我们只需要在输入数组上迭代,且索引 i 处的值为:L[i] * R[i]。
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int n = nums.size();
vector<int> multiNums(n);
vector<int> left(n, 0);
vector<int> right(n, 0);
left[0] = 1;
for (int i = 1; i < n; i++) {
// 此元素左侧所有乘积,为上一个left的总乘积,再乘以它左边的这个元素
left[i] = left[i - 1] * nums[i - 1];
}
right[n - 1] = 1;
for (int j = n - 2; j >= 0; j--) {
// 元素右边乘积,为之前的总乘积数值,再乘以其右边元素
right[j] = right[j + 1] * nums[j + 1];
}
for (int i = 0; i < n; i++) {
multiNums[i] = left[i] * right[i];
}
return multiNums;
}
};
加油站
在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
给定两个整数数组 gas 和 cost ,如果你可以按顺序绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1 。如果存在解,则 保证 它是 唯一 的。
示例 1:
输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
输出: 3
解释:
从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
因此,3 可为起始索引。
示例 2:
输入: gas = [2,3,4], cost = [3,4,3]
输出: -1
解释:
你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。
我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油
开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油
你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。
因此,无论怎样,你都不可能绕环路行驶一周。
提示:
n == gas.length == cost.length
1 <= n <= 105
0 <= gas[i], cost[i] <= 104
输入保证答案唯一。
思路1 嵌套循环(时间超限制)
构建了两个临时列表,gasExt和costExt,分别是gas和cost的扩展列表,长度为2n。方便从不同索引位置开始走一轮。
每到一个站点,都计算一次剩余油量,小于0就说明从这个站点出发不能走完全程,尝试下一个站点。如果剩余油量大于等于0,说明走完一轮了。
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
int n = gas.size();
vector<int> gasExt = {};
gasExt.insert(gasExt.end(), gas.begin(), gas.end());
gasExt.insert(gasExt.end(), gas.begin(), gas.end());
vector<int> costExt = {};
costExt.insert(costExt.end(), cost.begin(), cost.end());
costExt.insert(costExt.end(), cost.begin(), cost.end());
for (int i = 0; i < n; i++) {
int gasRemain = 0;
// 尝试从位置0出发,计算本轮的耗油量
for (int j = i; j < n + i; j++) {
gasRemain = gasRemain + gasExt[j] - costExt[j];
// 中途不够了,开始下一轮
if (gasRemain < 0) {
break;
}
}
if (gasRemain < 0) {
continue;
}
// 油量足够,返回这个索引
if (gasRemain >= 0) {
return i;
}
}
return -1;
}
};
官方 贪心算法
待理解疏通:

class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
int n = gas.size();
int i = 0;
while (i < n) {
int sumOfGas = 0, sumOfCost = 0;
int cnt = 0;
while (cnt < n) {
int j = (i + cnt) % n;
sumOfGas += gas[j];
sumOfCost += cost[j];
if (sumOfCost > sumOfGas) {
break;
}
cnt++;
}
if (cnt == n) {
return i;
} else {
i = i + cnt + 1;
}
}
return -1;
}
};
分发糖果
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。
你需要按照以下要求,给这些孩子分发糖果:
每个孩子至少分配到 1 个糖果。
相邻两个孩子中,评分更高的那个会获得更多的糖果。
请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
示例 1:
输入:ratings = [1,0,2]
输出:5
解释:你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。
示例 2:
输入:ratings = [1,2,2]
输出:4
解释:你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果,这满足题面中的两个条件。
提示:
n == ratings.length
1 <= n <= 2 * 104
0 <= ratings[i] <= 2 * 104
左右各遍历一次取最大值
为了满足上述两个条件,一个常用且高效的解法是: 分别 从左到右 和 从右到左 遍历两次,确保两边相邻的约束都满足,然后取两边较大的那个值作为每个孩子最终的糖果数。
class Solution {
public:
int candy(vector<int>& ratings) {
int n = ratings.size(); // 获取孩子数量
// 初始化一个数组left,用于存储每个孩子从左到右比较时应该得到的糖果数
vector<int> left(n);
// 第一个孩子至少给1颗糖果
left[0] = 1;
// 从左到右遍历,处理递增序列
for (int i = 1; i < n; i++) {
if (ratings[i] > ratings[i - 1]) {
// 如果当前孩子评分比左边高,则糖果数比左边多1
left[i] = left[i - 1] + 1;
} else {
// 否则,当前孩子至少给1颗糖果
left[i] = 1;
}
}
// right变量记录从右到左遍历时当前孩子应得的糖果数
int right = 1;
// 初始总数为最后一个孩子的较大值(left和right的初始值)
// 做从右往左遍历过程中,把左侧的结果考虑进去,一起算出总结果
int count = max(right, left[n - 1]);
// 从右到左遍历,处理递减序列
for (int i = n - 2; i >= 0; i--) {
if (ratings[i] > ratings[i + 1]) {
// 如果当前孩子评分比右边高,则糖果数比右边多1
right = right + 1;
} else {
// 否则,当前孩子至少给1颗糖果
right = 1;
}
// 对于每个孩子,取左右两个方向计算值的较大者,保证同时满足两个条件
count += max(right, left[i]);
}
return count; // 返回总糖果数
}
};
接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
n == height.length
1 <= n <= 2 * 104
0 <= height[i] <= 105
实例1配图:

思路1 动态规划
对于下标 i,下雨后水能到达的最大高度等于下标 i 两边的最大高度的最小值,下标 i 处能接的雨水量等于下标 i 处的水能到达的最大高度减去 height[i]。
不能遍历到每一个下标处都遍历一次左右元素找最高值,这样时间复杂度就是O(n^2)了。可以利用 除自身以外数组的乘积 这题的思想,遍历多次,动态维护两个列表。
创建两个长度为 n 的数组 leftMax 和 rightMax 。对于 0≤i<n ,leftMax[i] 表示下标 i 及其左边的位置中,height 的最大高度,rightMax[i] 表示下标 i 及其右边的位置中,height 的最大高度。
显然,leftMax[0]=height[0],rightMax[n−1]=height[n−1] 。两个数组的其余元素的计算如下:
当 1≤i≤n−1 时,leftMax[i]=max(leftMax[i−1],height[i]);
当 0≤i≤n−2 时,rightMax[i]=max(rightMax[i+1],height[i])。
因此可以正向遍历数组 height 得到数组 leftMax 的每个元素值,反向遍历数组 height 得到数组 rightMax 的每个元素值。
在得到数组 leftMax 和 rightMax 的每个元素值之后,对于 0≤i<n ,下标 i 处能接的雨水量等于 min(leftMax[i],rightMax[i])−height[i]。遍历每个下标位置即可得到能接的雨水总量。
class Solution {
public:
int trap(vector<int>& height) {
int n = height.size();
int count = 0;
vector<int> leftMax(n);
vector<int> rightMax(n);
// 初始化leftMax数组,从左到右遍历,记录每个位置左边的最大高度
int leftMaxTemp = height[0];
for (int i = 0; i < n; i++) {
leftMaxTemp = max(leftMaxTemp, height[i]);
leftMax[i] = leftMaxTemp;
}
// 初始化rightMax数组,从右到左遍历,记录每个位置右边的最大高度
int rightMaxTemp = height[n - 1];
for (int i = n - 1; i >= 0; i--) {
rightMaxTemp = max(rightMaxTemp, height[i]);
rightMax[i] = rightMaxTemp;
}
// 计算每个位置的接水量,累加得到总接水量
for (int i = 0; i < n; i++) {
int currentRain = min(rightMax[i], leftMax[i]) - height[i];
if (currentRain < 0) {
currentRain = 0;
}
count += currentRain;
}
return count;
}
};
小结
对于这种需要看 元素自身和其他所有元素的相对关系 的算法题,可以参考这两题的解法,还有分发糖果题目也是如此,左右各遍历一遍,取最大或者最小值,作为最终的正确结果。
罗马数字转整数
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1 。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I 可以放在 V (5) 和 X (10) 的左边,来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边,来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边,来表示 400 和 900。
给定一个罗马数字,将其转换成整数。
示例 1:
输入: s = "III"
输出: 3
示例 2:
输入: s = "IV"
输出: 4
示例 3:
输入: s = "IX"
输出: 9
示例 4:
输入: s = "LVIII"
输出: 58
解释: L = 50, V= 5, III = 3.
示例 5:
输入: s = "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.
提示:
1 <= s.length <= 15
s 仅含字符 ('I', 'V', 'X', 'L', 'C', 'D', 'M')
题目数据保证 s 是一个有效的罗马数字,且表示整数在范围 [1, 3999] 内
题目所给测试用例皆符合罗马数字书写规则,不会出现跨位等情况。
IL 和 IM 这样的例子并不符合题目要求,49 应该写作 XLIX,999 应该写作 CMXCIX 。
关于罗马数字的详尽书写规则,可以参考 罗马数字 - 百度百科。
思路1 模拟
通常情况下,罗马数字中小的数字在大的数字的右边。若输入的字符串满足该情况,那么可以将每个字符视作一个单独的值,累加每个字符对应的数值即可。
例如 XXVII 可视作 X+X+V+I+I=10+10+5+1+1=27。
即一般都是大数在左边,小数在右边,所以可以直接累加每个字符对应的数值,若一个数字右侧的数字比它大,则将该数字的符号取反。
例如 XIV 可视作 X−I+V=10−1+5=14。
class Solution {
private:
unordered_map<char, int> numMap = {
{'I', 1}, {'V', 5}, {'X', 10}, {'L', 50},
{'C', 100}, {'D', 500}, {'M', 1000},
};
public:
int romanToInt(string s) {
int n = s.size();
int num = 0;
int count = 0;
for (int i = 0; i < n - 1; i++) {
if (numMap[s[i]] < numMap[s[i + 1]]) {
count -= numMap[s[i]];
} else {
count += numMap[s[i]];
}
}
count += numMap[s[n - 1]];
return count;
}
};
整数转罗马数字
七个不同的符号代表罗马数字,其值如下:
符号 值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
罗马数字是通过添加从最高到最低的小数位值的转换而形成的。将小数位值转换为罗马数字有以下规则:
如果该值不是以 4 或 9 开头,请选择可以从输入中减去的最大值的符号,将该符号附加到结果,减去其值,然后将其余部分转换为罗马数字。
如果该值以 4 或 9 开头,使用 减法形式,表示从以下符号中减去一个符号,例如 4 是 5 (V) 减 1 (I): IV ,9 是 10 (X) 减 1 (I):IX。仅使用以下减法形式:4 (IV),9 (IX),40 (XL),90 (XC),400 (CD) 和 900 (CM)。
只有 10 的次方(I, X, C, M)最多可以连续附加 3 次以代表 10 的倍数。你不能多次附加 5 (V),50 (L) 或 500 (D)。如果需要将符号附加4次,请使用 减法形式。
给定一个整数,将其转换为罗马数字。
示例 1:
输入:num = 3749
输出: "MMMDCCXLIX"
解释:
3000 = MMM 由于 1000 (M) + 1000 (M) + 1000 (M)
700 = DCC 由于 500 (D) + 100 (C) + 100 (C)
40 = XL 由于 50 (L) 减 10 (X)
9 = IX 由于 10 (X) 减 1 (I)
注意:49 不是 50 (L) 减 1 (I) 因为转换是基于小数位
示例 2:
输入:num = 58
输出:"LVIII"
解释:
50 = L
8 = VIII
示例 3:
输入:num = 1994
输出:"MCMXCIV"
解释:
1000 = M
900 = CM
90 = XC
4 = IV
提示:
1 <= num <= 3999
思路1 遍历搜索法
维护四个map,对应从个位到千位上0-9的罗马数字。解析出每个位上的数字,根据罗马数字的规则,将其转换为罗马数字。
const string thousands[] = {"", "M", "MM", "MMM"};
const string hundreds[] = {"", "C", "CC", "CCC", "CD",
"D", "DC", "DCC", "DCCC", "CM"};
const string tens[] = {"", "X", "XX", "XXX", "XL",
"L", "LX", "LXX", "LXXX", "XC"};
const string ones[] = {"", "I", "II", "III", "IV",
"V", "VI", "VII", "VIII", "IX"};
class Solution {
public:
string intToRoman(int num) {
int thousand = num / 1000;
int hundred = num % 1000 / 100;
int ten = num % 100 / 10;
int unit = num % 10;
return thousands[thousand] + hundreds[hundred] +
tens[ten] + ones[unit];
}
};
最后一个单词的长度
给你一个字符串 s,由若干单词组成,单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。
单词 是指仅由字母组成、不包含任何空格字符的最大子字符串。
示例 1:
输入:s = "Hello World"
输出:5
解释:最后一个单词是“World”,长度为 5。
示例 2:
输入:s = " fly me to the moon "
输出:4
解释:最后一个单词是“moon”,长度为 4。
示例 3:
输入:s = "luffy is still joyboy"
输出:6
解释:最后一个单词是长度为 6 的“joyboy”。
提示:
1 <= s.length <= 104
s 仅有英文字母和空格 ' ' 组成
s 中至少存在一个单词
思路1 kotlin速通
使用扩展函数可以光速解题:
class Solution {
fun lengthOfLastWord(s: String) = s.split(" ").filter{it.isNotEmpty()}.last().length
}
思路2 使用两个标记位记录位置
从后往前倒序遍历 ,记录下第一个有效非空字符和第一个有效字符之前的空格位置,计算二者差值即为长度;处理一下字符串一开始就是有效字符的边界情况。
class Solution {
public:
int lengthOfLastWord(string s) {
int n = s.size();
int lastNotEmpty = -1;
int lastSpaceBeforeString = -1;
int size = 0;
for (int i = n - 1; i >= 0; i--) {
if (s[i] != ' ' && lastNotEmpty == -1) {
lastNotEmpty = i;
}
if (s[i] == ' ' && lastNotEmpty != -1) {
lastSpaceBeforeString = i;
size = lastNotEmpty - lastSpaceBeforeString;
break;
}
// 处理开头就是有效位的情况
if (i == 0 && lastSpaceBeforeString == -1) {
size = lastNotEmpty + 1;
}
}
return size;
}
};
最长公共前缀
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""。
示例 1:
输入:strs = ["flower","flow","flight"]
输出:"fl"
示例 2:
输入:strs = ["dog","racecar","car"]
输出:""
解释:输入不存在公共前缀。
提示:
1 <= strs.length <= 200
0 <= strs[i].length <= 200
strs[i] 如果非空,则仅由小写英文字母组成
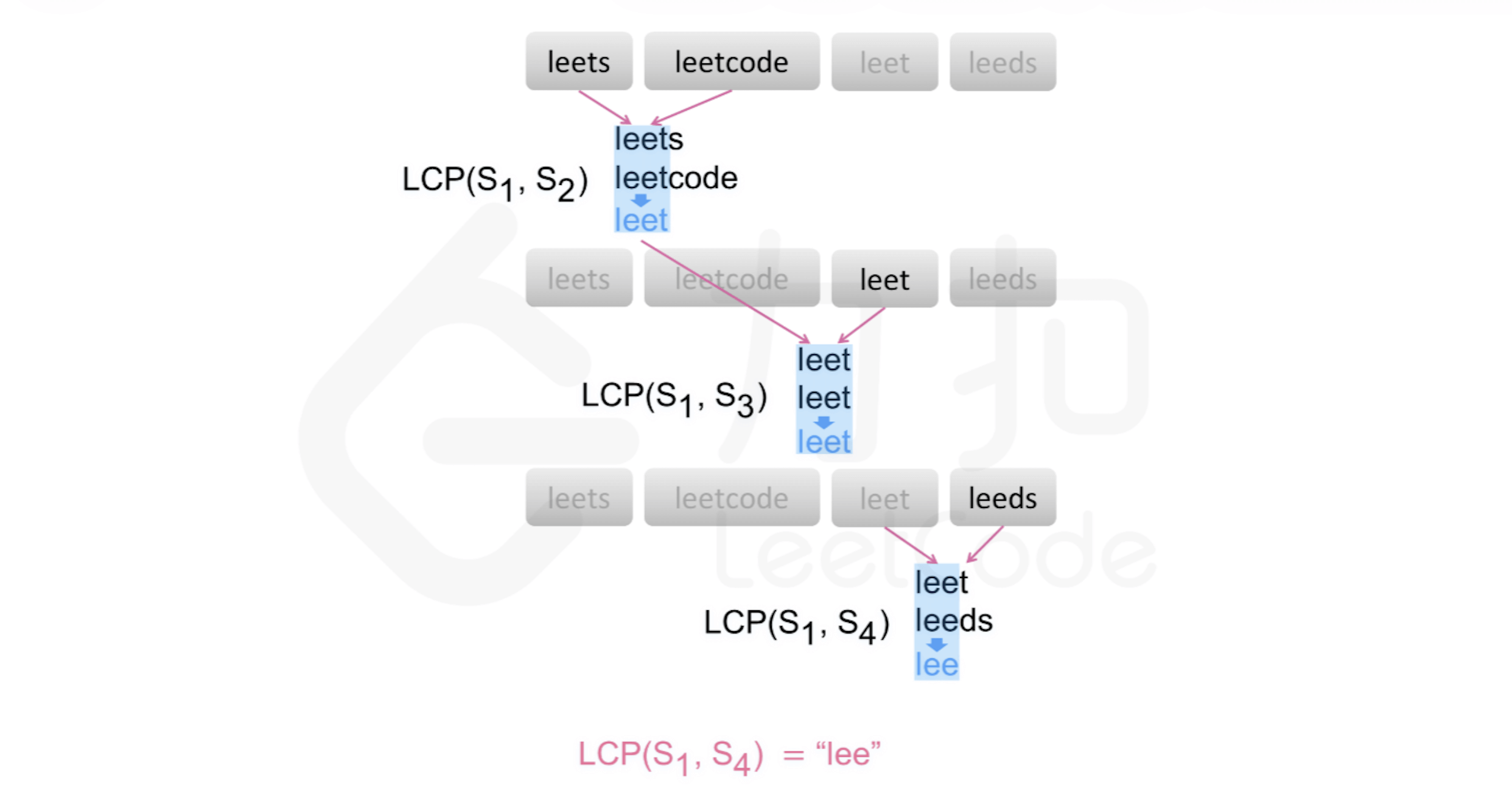
思路1 水平扫描
从前往后遍历字符串数组中的每个字符串,对于每个遍历到的字符串,更新最长公共前缀,当遍历完所有的字符串以后,即可得到字符串数组中的最长公共前缀。
如果在尚未遍历完所有的字符串时,最长公共前缀已经是空串,则最长公共前缀一定是空串,因此不需要继续遍历剩下的字符串,直接返回空串即可。
class Solution {
public:
string longestCommonPrefix(vector<string>& strs) {
int n = strs.size();
if (n == 0) {
return "";
}
string longestPrefix = strs[0];
for (int i = 1; i < n; i++) {
string commonPrefix = commonPrefixBetweenPair(longestPrefix, strs[i]);
longestPrefix = commonPrefix;
if (longestPrefix == "") {
break;
}
}
return longestPrefix;
}
string commonPrefixBetweenPair(string& s1, string& s2) {
int n = min(s1.size(), s2.size());
int index = 0;
while (index <= n && s1[index] == s2[index]) {
index++;
}
return s1.substr(0, index);
}
};
151. 反转字符串中的单词
给你一个字符串 s ,请你反转字符串中 单词 的顺序。
单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。
注意:输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中,单词间应当仅用单个空格分隔,且不包含任何额外的空格。
示例 1:
输入:s = "the sky is blue"
输出:"blue is sky the"
示例 2:
输入:s = " hello world "
输出:"world hello"
解释:反转后的字符串中不能存在前导空格和尾随空格。
示例 3:
输入:s = "a good example"
输出:"example good a"
解释:如果两个单词间有多余的空格,反转后的字符串需要将单词间的空格减少到仅有一个。
提示:
1 <= s.length <= 104
s 包含英文大小写字母、数字和空格 ' '
s 中 至少存在一个 单词
进阶:如果字符串在你使用的编程语言中是一种可变数据类型,请尝试使用 O(1) 额外空间复杂度的 原地 解法。
kotlin 速通
先分割倒序,再插入空格拼接。
class Solution {
fun reverseWords(s: String)=s.split(" ").filter{it.isNotEmpty()}.reversed().joinToString(" ");
}
joinToString 用于将集合中的元素连接成一个字符串,返回一个新的字符串。可以指定连接符、前缀、后缀等。
思路1 拆出每一个单词填入一个新的数组,最后倒序遍历拼接
首先去除字符串首尾的空格,然后从前往后遍历字符串,找到每个单词的起始位置和结束位置,将每个单词填入一个新的数组,最后倒序遍历数组拼接单词即可。
class Solution {
public:
string reverseWords(string s) {
int n = s.size();
vector<string> validateWords(n);
int left = 0;
int right = n - 1;
string result = "";
// 去掉字符串开头的空白字符
while (left <= right && s[left] == ' ')
++left;
// 去掉字符串末尾的空白字符
while (left <= right && s[right] == ' ')
--right;
string word = "";
int count = 0;
// left指向第一个有效单次起始位置,right指向最后一个单词末尾位置
while (left <= right) {
char c = s[left];
if (c != ' ') {
word += c;
} else if (word.size() > 0 && c == ' ') {
validateWords[count] = word;
word = "";
count++;
}
left++;
}
validateWords[count] = word;
count++;
for (int i = count-1; i >= 0; i--) {
result += validateWords[i];
if (i != 0) {
result += " ";
}
}
return result;
}
};
将存放单词的 vector 换成 stack 实现,可以不用维护 count 这个标记:
class Solution {
public:
string reverseWords(string s) {
int n = s.size();
stack<string> validateWords;
int left = 0;
int right = n - 1;
string result = "";
// 去掉字符串开头的空白字符
while (left <= right && s[left] == ' ')
++left;
// 去掉字符串末尾的空白字符
while (left <= right && s[right] == ' ')
--right;
string word = "";
// left指向第一个有效单次起始位置,right指向最后一个单词末尾位置
while (left <= right) {
char c = s[left];
if (c != ' ') {
word += c;
} else if (word.size() > 0 && c == ' ') {
validateWords.push(word);
word = "";
}
left++;
}
validateWords.push(word);
while (!validateWords.empty()) {
result += validateWords.top();
validateWords.pop();
if (!validateWords.empty()) {
result += " ";
}
}
return result;
}
};
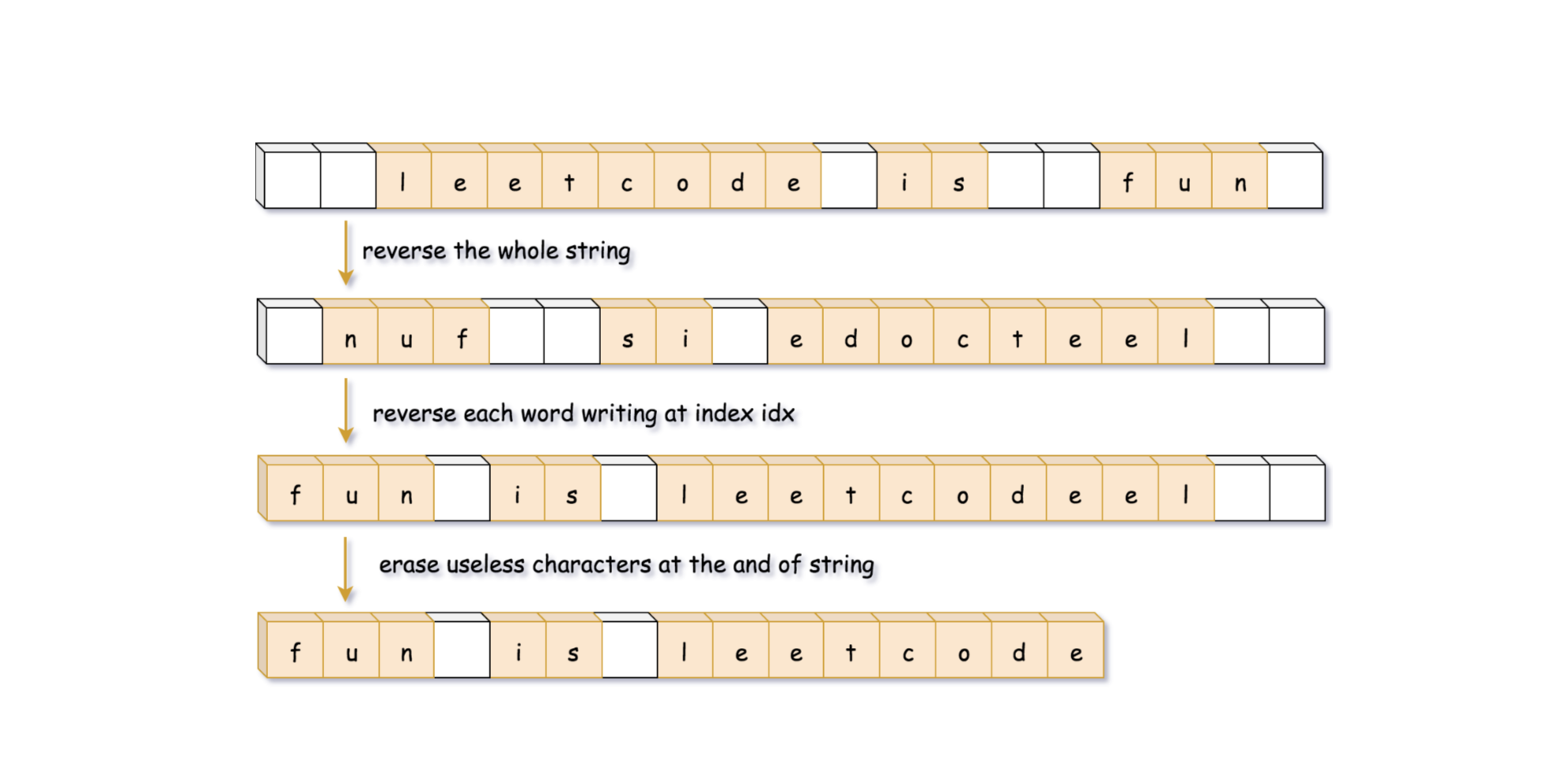
思路2 直接操作原字符串
操作原字符串,先将整个字符串反转,然后在遍历的过程中,消减空格,将遇到的每个单词反转,最后去除末尾多余的空格。
class Solution {
public:
string reverseWords(string s) {
// 反转整个字符串
reverse(s.begin(), s.end());
int n = s.size();
int idx = 0;
for (int start = 0; start < n; ++start) {
if (s[start] != ' ') {
// 填一个空白字符然后将idx移动到下一个单词的开头位置
if (idx != 0) s[idx++] = ' ';
// 循环遍历至单词的末尾
int end = start;
while (end < n && s[end] != ' ') s[idx++] = s[end++];
// 反转整个单词
reverse(s.begin() + idx - (end - start), s.begin() + idx);
// 更新start,去找下一个单词
start = end;
}
}
s.erase(s.begin() + idx, s.end());
return s;
}
};
Z 字形变换
将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 "PAYPALISHIRING" 行数为 3 时,排列如下:
P A H N
A P L S I I G
Y I R
之后,你的输出需要从左往右逐行读取,产生出一个新的字符串,比如:"PAHNAPLSIIGYIR"。
请你实现这个将字符串进行指定行数变换的函数:
string convert(string s, int numRows);
示例 1:
输入:s = "PAYPALISHIRING", numRows = 3
输出:"PAHNAPLSIIGYIR"
示例 2:
输入:s = "PAYPALISHIRING", numRows = 4
输出:"PINALSIGYAHRPI"
解释:
P I N
A L S I G
Y A H R
P I
示例 3:
输入:s = "A", numRows = 1
输出:"A"
提示:
1 <= s.length <= 1000
s 由英文字母(小写和大写)、',' 和 '.' 组成
1 <= numRows <= 1000
官方题解 二维矩阵模拟

class Solution {
public:
string convert(string s, int numRows) {
int n = s.length(), r = numRows;
if (r == 1 || r >= n) {
return s;
}
int t = r * 2 - 2;
int c = (n + t - 1) / t * (r - 1);
vector<string> mat(r, string(c, 0));
for (int i = 0, x = 0, y = 0; i < n; ++i) {
mat[x][y] = s[i];
if (i % t < r - 1) {
++x; // 向下移动
} else {
--x;
++y; // 向右上移动
}
}
string ans;
for (auto &row : mat) {
for (char ch : row) {
if (ch) {
ans += ch;
}
}
}
return ans;
}
};
思路1 顺序填入,控制转向
不用在意元素的处于转换矩阵中的哪一列,只需要关注元素的处于转换矩阵中的哪一行。 将字符串元素按照Z形填入,就是从上往下填到最后一行 (numRows - 1) 的元素就转向,从下往上填,等填到最上面一行 (0) 了,接下来就再往下。
class Solution {
public:
string convert(string s, int numRows) {
int n = s.size();
if (numRows == 1 || n < numRows) {
return s;
}
// 预存矩阵,存放每一行的结果
vector<string> rows(numRows);
// 转向标志位,触底和触顶反弹
int trunFlag = 1;
int index = 0;
for (int i = 0; i < n; i++) {
rows[index].push_back(s[i]);
// 更新下一个元素下标
index += trunFlag;
// 达到转向条件,变向
if (index == numRows - 1 || index == 0) {
trunFlag = -trunFlag;
}
}
string result;
for (auto row : rows) {
result += row;
}
return result;
}
};
找出字符串的第一个匹配项下标
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
示例 1:
输入:haystack = "sadbutsad", needle = "sad"
输出:0
解释:"sad" 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ,所以返回 0 。
示例 2:
输入:haystack = "leetcode", needle = "leeto"
输出:-1
解释:"leeto" 没有在 "leetcode" 中出现,所以返回 -1 。
提示:
1 <= haystack.length, needle.length <= 104
haystack 和 needle 仅由小写英文字符组成
思路1 借用找前缀那一题的思想
对 haystack 字符串进行遍历,找到第一个匹配的字符,判断以这个字符下标 i 为起始位置的子字符串是否和 needle 字符串为前缀重合的字符串。
将原问题简化为判断子字符串是否和 needle 字符串为前缀重合。
class Solution {
public:
int strStr(string haystack, string needle) {
int longLenth = haystack.size();
int shortLenth = needle.size();
// 长度判断,子串更长,直接判错
if (longLenth < shortLenth) {
return -1;
}
for (int i = 0; i < longLenth; i++) {
if (haystack[i] == needle[0]) {
string cmp = haystack.substr(i, longLenth - i);
// 找到公共前缀,返回下标
if (findCommonPrefix(cmp, needle)) {
return i;
}
}
}
// 遍历完都没有找到公共前缀,返回-1
return -1;
}
// 找公共前缀
bool findCommonPrefix(string& s1, string& s2) {
int n = s2.size();
for (int i = 0; i < n; i++) {
if (s1[i] != s2[i]) {
return false;
}
}
return true;
}
};
直接使用find函数
做完基础校验后,直接使用库函数 find 查找子字符串 needle 是否存在于 haystack 中。
class Solution {
public:
int strStr(string haystack, string needle) {
int longLenth = haystack.size();
int shortLenth = needle.size();
// 长度判断,子串更长,直接判错
if (longLenth < shortLenth) {
return -1;
}
// 直接使用库函数
size_t pos = haystack.find(needle);
if (pos != string::npos) {
return pos;
} else {
return -1;
}
}
};
文本左右对齐
给定一个单词数组 words 和一个长度 maxWidth ,重新排版单词,使其成为每行恰好有 maxWidth 个字符,且左右两端对齐的文本。
你应该使用 “贪心算法” 来放置给定的单词;也就是说,尽可能多地往每行中放置单词。必要时可用空格 ' ' 填充,使得每行恰好有 maxWidth 个字符。
要求尽可能均匀分配单词间的空格数量。如果某一行单词间的空格不能均匀分配,则左侧放置的空格数要多于右侧的空格数。
文本的最后一行应为左对齐,且单词之间不插入额外的空格。
注意:
单词是指由非空格字符组成的字符序列。
每个单词的长度大于 0,小于等于 maxWidth。
输入单词数组 words 至少包含一个单词。
示例 1:
输入: words = ["This", "is", "an", "example", "of", "text", "justification."], maxWidth = 16
输出:
[
"This is an",
"example of text",
"justification. "
]
示例 2:
输入:words = ["What","must","be","acknowledgment","shall","be"], maxWidth = 16
输出:
[
"What must be",
"acknowledgment ",
"shall be "
]
解释: 注意最后一行的格式应为 "shall be " 而不是 "shall be",
因为最后一行应为左对齐,而不是左右两端对齐。
第二行同样为左对齐,这是因为这行只包含一个单词。
示例 3:
输入:words = ["Science","is","what","we","understand","well","enough","to","explain","to","a","computer.","Art","is","everything","else","we","do"],maxWidth = 20
输出:
[
"Science is what we",
"understand well",
"enough to explain to",
"a computer. Art is",
"everything else we",
"do "
]
提示:
1 <= words.length <= 300
1 <= words[i].length <= 20
words[i] 由小写英文字母和符号组成
1 <= maxWidth <= 100
words[i].length <= maxWidth
思路1 模拟

class Solution {
// blank 返回长度为 n 的由空格组成的字符串
string blank(int n) {
return string(n, ' ');
}
// join 返回用 sep 拼接 [left, right) 范围内的 words 组成的字符串
string join(vector<string> &words, int left, int right, string sep) {
string s = words[left];
for (int i = left + 1; i < right; ++i) {
s += sep + words[i];
}
return s;
}
public:
vector<string> fullJustify(vector<string> &words, int maxWidth) {
vector<string> ans;
int right = 0, n = words.size();
while (true) {
int left = right; // 当前行的第一个单词在 words 的位置
int sumLen = 0; // 统计这一行单词长度之和
// 循环确定当前行可以放多少单词,注意单词之间应至少有一个空格
while (right < n && sumLen + words[right].length() + right - left <= maxWidth) {
sumLen += words[right++].length();
}
// 当前行是最后一行:单词左对齐,且单词之间应只有一个空格,在行末填充剩余空格
if (right == n) {
string s = join(words, left, n, " ");
ans.emplace_back(s + blank(maxWidth - s.length()));
return ans;
}
int numWords = right - left;
int numSpaces = maxWidth - sumLen;
// 当前行只有一个单词:该单词左对齐,在行末填充剩余空格
if (numWords == 1) {
ans.emplace_back(words[left] + blank(numSpaces));
continue;
}
// 当前行不只一个单词
int avgSpaces = numSpaces / (numWords - 1);
int extraSpaces = numSpaces % (numWords - 1);
string s1 = join(words, left, left + extraSpaces + 1, blank(avgSpaces + 1)); // 拼接额外加一个空格的单词
string s2 = join(words, left + extraSpaces + 1, right, blank(avgSpaces)); // 拼接其余单词
ans.emplace_back(s1 + blank(avgSpaces) + s2);
}
}
};
字符串表示的数字相加
给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和并同样以字符串形式返回。
你不能使用任何內建的用于处理大整数的库(比如 BigInteger), 也不能直接将输入的字符串转换为整数形式。
示例 1:
输入:num1 = "11", num2 = "123"
输出:"134"
示例 2:
输入:num1 = "456", num2 = "77"
输出:"533"
示例 3:
输入:num1 = "0", num2 = "0"
输出:"0"
提示:
1 <= num1.length, num2.length <= 104
num1 和num2 都只包含数字 0-9
num1 和num2 都不包含任何前导零
思路1 库函数
std::stoi() 函数可以将字符串转换为整数。 std::to_string() 函数可以将整数转换为字符串。
class Solution {
public:
string addStrings(string num1, string num2) {
return to_string(stoi(num1) + stoi(num2));
}
};
在超出int范围会溢出。
模拟手工加法
从最低位到高位倒序遍历,对两个字符串数字的每一位进行加法运算,结果存储在一个新的字符串中。注意处理进位,超出10的进位在下一次遍历中加进去。
class Solution {
public:
string addStrings(string num1, string num2) {
int i = num1.size() - 1;
int j = num2.size() - 1;
int carry = 0;
string result = "";
// 从右往左逐位相加
while (i >= 0 || j >= 0 || carry > 0) {
// 和字符0的ASCII值相减,得到当前位的数字int值
int digit1 = (i >= 0) ? num1[i] - '0' : 0;
int digit2 = (j >= 0) ? num2[j] - '0' : 0;
// 计算当前位的和,注意要加上上一次的进位
int sum = digit1 + digit2 + carry;
carry = sum / 10; // 和大于10再进位
int current_digit = sum % 10; // 当前位取余数加到结果中
result.push_back(current_digit + '0');
i--;
j--;
}
// 反转结果字符串
reverse(result.begin(), result.end());
return result;
}
};
最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1]
输出:1
示例 3:
输入:nums = [5,4,-1,7,8]
输出:23
提示:
1 <= nums.length <= 105
-104 <= nums[i] <= 104
进阶:如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的 分治法 求解。
思路1 动态规划
这题乍一看需要像是滑动窗口求解,但是数组无序,且不能改变元素顺序。所以无法判断滑动窗口的移动条件。
应该使用动态规划求解。
假设 nums 数组的长度是 n,下标从 0 到 n−1。
我们用 f(i) 代表以第 i 个数结尾的「连续子数组的最大和」,那么很显然我们要求的答案就是: \(\max_{0 \leq i \leq n-1} f(i)\)
因此我们只需要求出每个位置的 f(i),然后返回 f 数组中的最大值即可。 那么我们如何求 f(i) 呢? 我们可以考虑 nums[i] 单独成为一段还是加入 f(i−1) 对应的那一段,这取决于 nums[i] 和 f(i−1)+nums[i] 的大小,我们希望获得一个比较大的,于是可以写出这样的动态规划转移方程:
f(i)=max{f(i−1)+nums[i],nums[i]}
不难给出一个时间复杂度 O(n)、空间复杂度 O(n) 的实现,即用一个 f 数组来保存 f(i) 的值,用一个循环求出所有 f(i)。考虑到 f(i) 只和 f(i−1) 相关,于是我们可以只用一个变量 pre 来维护对于当前 f(i) 的 f(i−1) 的值是多少,从而让空间复杂度降低到 O(1),这有点类似 「滚动数组」 的思想。
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int maxSum = nums[0];
int currentSum = nums[0];
for (int i = 1; i < nums.size(); i++) {
currentSum = max(nums[i], currentSum + nums[i]);
maxSum = max(maxSum, currentSum);
}
return maxSum;
}
};
字母异位词分组
给你一个字符串数组,请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
示例 1:
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]
解释:
在 strs 中没有字符串可以通过重新排列来形成 "bat"。
字符串 "nat" 和 "tan" 是字母异位词,因为它们可以重新排列以形成彼此。
字符串 "ate" ,"eat" 和 "tea" 是字母异位词,因为它们可以重新排列以形成彼此。
示例 2:
输入: strs = [""]
输出: [[""]]
示例 3:
输入: strs = ["a"]
输出: [["a"]]
提示:
1 <= strs.length <= 104
0 <= strs[i].length <= 100
strs[i] 仅包含小写字母
思路1 hash表对比
每个元素都是一个字符串,如果两个元素是互为异位词,这两个字符串排序之后的结果一定相同,可以将排序后的结果设为 key ,value就为一个string的动态数组,有相同的直接推送到value里面。最后取出来加入到结果数组里。
class Solution {
public:
vector<vector<string>> groupAnagrams(vector<string>& strs) {
int n = strs.size();
// 最终结果
vector<vector<string>> ans;
// 用来对比的hash表
unordered_map<string, vector<string>> mp;
for (string& str : strs) {
string key = str;
sort(key.begin(), key.end());
// 排序后的字符串作为key,互为异位词的元素全部加进去
mp[key].emplace_back(str);
}
// 遍历hash表,填到结果数组里
for (auto it = mp.begin(); it != mp.end(); it++) {
ans.emplace_back(it->second);
}
return ans;
}
};
数组和字符串算法题总结
无论是数组还是字符串,在算法题中,它们本质上都是线性的数据结构。字符串可以看作是一个字符数组,因此很多数组的技巧同样适用于字符串。解题的核心在于高效地遍历和操作这些线性序列。
一、数组常见题型与解法
1. 双指针技巧
这是解决数组问题最常用、最核心的技巧之一,变化多端。
- 对撞指针:两个指针从两端向中间移动。
- 适用场景:
- 有序数组的二分查找。
- 两数之和、三数之和问题(当数组有序时)。
- 反转数组、判断回文。
- 示例:在一个有序数组中找出两个数,使它们的和为 target。
- 适用场景:
- 快慢指针:两个指针以不同速度移动。
- 适用场景:
- 判断链表是否有环(同样适用于数组的循环查找)。
- 原地删除有序数组中的重复项(LeetCode 26)。
- 移动零(LeetCode 283),将0移到数组末尾而不改变非零元素的相对顺序。
- 示例:
slow指针指向下一个非零元素该放的位置,fast指针遍历数组。
- 适用场景:
- 滑动窗口:双指针的一种特殊形式,维护一个窗口(子数组),通过移动左右指针来动态调整窗口大小。
- 适用场景:
- 寻找满足条件的最长/最短子数组或子字符串。
- 求和/乘积大于/小于某值的子数组个数。
- 关键:思考窗口何时扩大(右指针右移),何时收缩(左指针右移),以及如何更新结果。
- 示例:无重复字符的最长子串(LeetCode 3)、长度最小的子数组(LeetCode 209)。
- 适用场景:
2. 前缀和
用于快速、频繁地计算子数组的区间和。
- 核心思想:预处理一个
prefix数组,其中prefix[i]表示nums[0]到nums[i-1]的和(或nums[0]到nums[i],看定义)。 - 适用场景:
- 求任意区间
[i, j]的和,公式为prefix[j+1] - prefix[i]。 - 统计满足“子数组和为k”的子数组个数(常配合哈希表使用,记录前缀和出现的次数)。
- 求任意区间
- 示例:和为 K 的子数组(LeetCode 560)。
3. 模拟与数学
这类问题更考验对题意的理解和代码实现能力。
- 适用场景:
- 矩阵/二维数组的螺旋遍历(LeetCode 54)。
- 数组的旋转(LeetCode 189),常用多次反转的技巧。
- 下一个排列(LeetCode 31)。
- 寻找主元素(出现次数超过一半的元素,摩尔投票法)。
4. 哈希表
利用 std::unordered_map 或 std::unordered_set 实现 O(1) 时间复杂度的查找,是“空间换时间”的典范。
- 适用场景:
- 两数之和(LeetCode 1)的经典解法。
- 判断数组中是否存在重复元素。
- 与前缀和结合,解决“子数组和为k”的问题。
- 统计元素频率。
二、字符串常见题型与解法
字符串的很多技巧与数组相通,但也有其特殊性(如反转、子串匹配等)。
1. 双指针
- 适用场景:
- 判断回文串。
- 反转字符串(LeetCode 344)。
- 字符串压缩。
2. 滑动窗口
- 适用场景:
- 字符串的经典问题:无重复字符的最长子串(LeetCode 3)。
- 找到字符串中所有字母异位词(LeetCode 438)。
- 最小覆盖子串(LeetCode 76)。
3. 字符串匹配 - KMP 算法
用于解决子串查找问题。
- 核心思想:当匹配失败时,利用已匹配的信息(next数组/前缀表)跳过不必要的比较,将指针回退到合理的位置。
- 适用场景:
- 判断一个字符串是否是另一个字符串的子串。
- 重复的子字符串问题(LeetCode 459)。
4. 字符串操作与模拟
- 适用场景:
- 字符串转换整数 (atoi)(LeetCode 8)。
- 验证IP地址(LeetCode 468)。
- 字符串解码(LeetCode 394),常用栈来解决。
- 翻转字符串里的单词(LeetCode 151),综合运用反转和双指针。
5. 哈希表与计数
- 适用场景:
- 有效的字母异位词(LeetCode 242)。
- 找到所有字母异位词的起始索引(可与滑动窗口结合)。
- 第一个只出现一次的字符。
三、通用解题思路与技巧
- 排序是利器:很多复杂问题在排序后会变得简单(例如,双指针解决多数和问题)。但要注意排序是否会改变原始索引。
- 空间换时间:毫不犹豫地使用哈希表、辅助数组等来存储中间结果,这是优化时间复杂度的常用手段。
- 边界条件:数组/字符串为空、只有一个元素、所有元素相同等特殊情况一定要考虑。
- STL 的熟练运用:
vector: 动态数组,最常用。string: 提供了find,substr等方法,但要注意效率。unordered_map/unordered_set: 高效的哈希容器。stack/queue: 用于特定场景,如单调栈解决“下一个更大元素”问题。
- 复杂度分析:养成分析时间、空间复杂度的习惯,这有助于你选择最优解法。
总结表格
| 类别 | 常见题型 | 核心解决方式 |
|---|---|---|
| 数组 | 两数/三数之和、子数组和 | 排序+双指针、哈希表、前缀和 |
| 子数组问题(最大和、满足条件) | 滑动窗口、前缀和、动态规划(如最大子数组和) | |
| 去重、移动元素 | 快慢指针 | |
| 旋转、螺旋矩阵 | 模拟、数学技巧(多次反转) | |
| 字符串 | 回文、反转 | 双指针 |
| 无重复最长子串、字母异位词 | 滑动窗口 | |
| 子串查找/匹配 | KMP算法 | |
| 字符串解析、解码 | 模拟、栈 | |
| 异位词判断、字符计数 | 哈希表 |
最后建议:理论学习后,一定要去 LeetCode 或类似平台进行专题练习,将这些技巧内化为自己的解题能力。可以从“Top 100 Liked”问题列表开始,里面包含了大量数组和字符串的经典题目。
